26.7. Статистические игры

Рассмотренные выше игры часто называют стратегическими играми. В их основе лежит предположение о том, что каждый игрок действует активно и стремится, по возможности, использовать свою оптимальную стратегию для получения наибольшего выигрыша.

Однако во многих практических ситуациях один из игроков оказывается нейтральным и не стремится извлечь максимальной выгоды. В качестве такого игрока часто выступает природа, т.е. совокупность внешних обстоятельств, в которых приходится принимать решение.

Природа не имеет злого умысла по отношению к человеку и не стремится нанести ему ущерб. Она просто действует и развивается в соответствии со своими законами. Если бы человек точно знал законы природы, он мог бы их использовать с максимальной пользой. Однако во многих случаях человек не знает законов природы или знает их недостаточно точно. В такой ситуации неполной информации о законах природы существует возможность принятия ошибочных решений.

Игры, в которых одним противником является природа, а другим человек, получили название статистических игр. Обычно человека, участвующего в игре против природы, называют статистиком. Будем считать природу первым игроком, а статистика – вторым (игроком В).

Пусть имеется некоторое множество возможных состояний природы П₁, П₂, … , П_m. Обозначим возможные решения (стратегии) статистика B₁, B₂, … , B_n. При выборе какой-то стратегии статистик может потерпеть убыток a_ij, зависящий как от выбранной им стратегии B_j, так и от состояния П_i, которое примет природа.

Пусть известны все значения a_ij. Тогда матрица игры (часто называемая матрицей последствий или матрицей потерь) может быть записана либо в виде таблицы

П	В
	B1	В2	…	Вn
П1	a11	a12	…	a1n
П2	a21	a22	…	a2n
…	…	…	…	…
Пm	am1	am2	…	amn

либо в виде обычной матрицы:

.

Иногда при решении статистической игры используется матрица рисков. Элементы r_ij матрицы рисков равны разности между тем убытком, который статистик получит, выбирая стратегию B_j, и минимально возможным убытком при том же состоянии природы П_i:

.

Если не известно, с какими вероятностями природа принимает состояния П₁, П₂, … П_m, то говорят, что решение принимается в условиях полной неопределенности. При этом для выбора оптимальной стратегии статистика можно использовать несколько правил.

Правило Вальда. За оптимальную принимается стратегия, которая в наихудших условиях гарантирует минимальный проигрыш, т.е. стратегия, соответствующая верхней цене игры :

.

Правило Сэвиджа. Рекомендуется выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается

.

Правила Вальда и Сэвиджа ориентируют статистика на самые неблагоприятные состояния природы, т.е. эти правила выражают пессимистическую оценку ситуации.

Правило Гурвица является правилом пессимизма-оптимизма. За оптимальную принимается та стратегия, для которой выполняется соотношение:

,

где 0    1.

При  = 0 имеем критерий крайнего оптимизма, а при  = 1 – критерий пессимизма Вальда. При промежуточных значениях 0 <  < 1 имеем нечто среднее. Для страховки обычно  принимают близким к единице. В общем случае число  выбирают, исходя из опыта.

Пример. Задача о замене оборудования.

Установленное на предприятии оборудование после 5 лет работы может оказаться в одном из трех состояний:

П₁ – оборудование вполне работоспособно и требует лишь небольшого текущего ремонта.

П₂ – некоторые детали значительно износились и требуют серьезного ремонта или замены.

П₃ – основные детали износились настолько, что дальнейшая эксплуатация оборудования невозможна.

Для предприятия возможны три различных способа действия:

В₁ – оставить оборудование в работе еще на год, проведя незначительный ремонт своими силами.

В₂ – провести капитальный ремонт оборудования с вызовом специальной бригады ремонтников.

В₃ – заменить оборудование новым.

Потери, которые несет предприятие при различных способах действия, приведены в таблице в относительных денежных единицах. В потери входят стоимость ремонта или замены оборудования, а также убытки, связанные с ухудшением качества продукции и с простоями, вызванными неисправным оборудованием.

Пi	Вj
	В1	В2	В3
П1	1	3	5
П2	5	2	4
П3	7	6	3

Требуется найти оптимальный способ действий для предприятия.

Решение.

а) Правило Вальда. Найдем в каждом столбце таблицы наибольшее значение, а из всех наибольших выберем наименьшее . Стратегия, соответствующая , будет оптимальным способом действий предприятия по правилу Вальда.

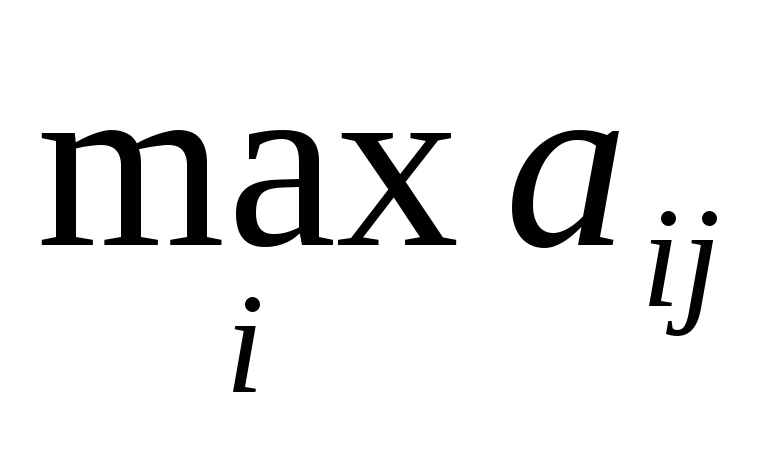
7

6

5

 = 5

Отсюда следует, что оптимальной стратегией является стратегия В₃.

б) Правило Сэвиджа. На основе матрицы последствий по формуле

составим матрицу рисков:

Пi	Вj
	В1	В2	В3
П1	0	2	4
П2	3	0	2
П3	4	3	0

Найдем в каждом столбце таблицы наибольшее значение, а из всех наибольших выберем наименьшее . Стратегия, соответствующая этому значению, будет оптимальным способом действий предприятия по правилу Сэвиджа.

4

3

4

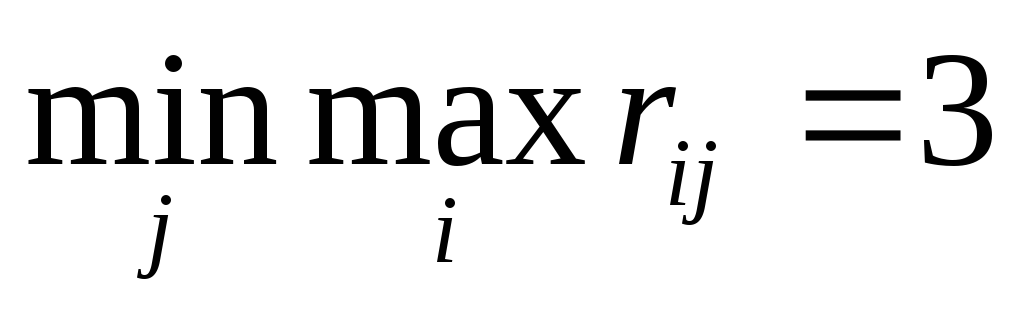
Отсюда следует, что оптимальной стратегией является стратегия В₂.

в) Правило Гурвица. Рассмотрим оптимистический ( = 0) и оптимистическо-пессимистический ( = 0,5) случаи. При  = 1 правило Гурвица совпадает с правилом Вальда.

 = 0.

Найдем . Для этого в матрице последствий в каждом столбце найдем наименьшее значение и из них выберем наименьшее.

1

2

3

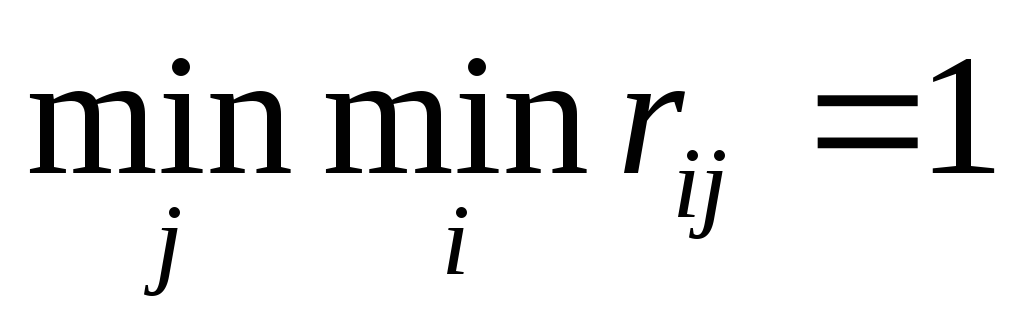
Отсюда видно, что оптимальной стратегией является стратегия В₁.

 = 0,5.

Найдем .

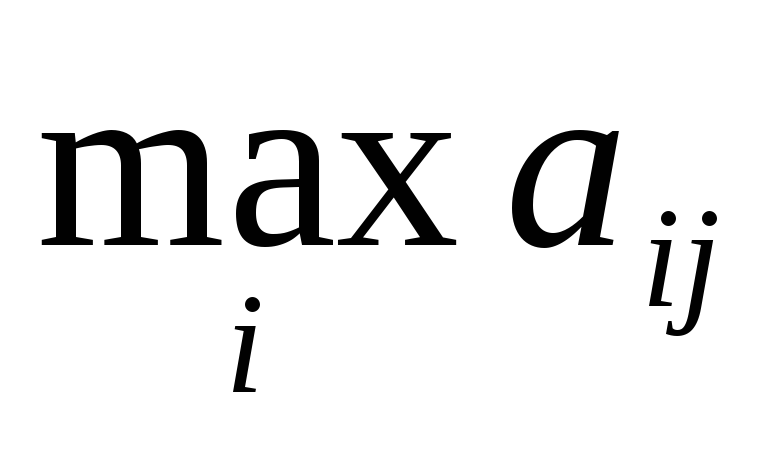
	7	6	5
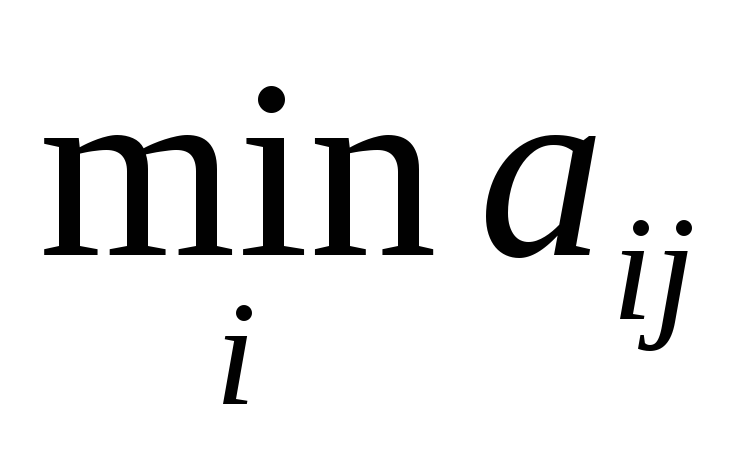
	1	2	3
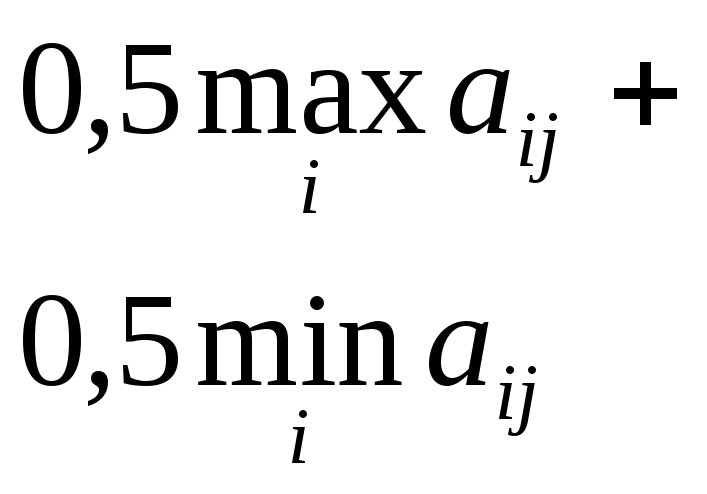
	4	4	4

Отсюда видно, что все стратегии предприятия равнозначны.

В статистической игре из прошлого опыта может быть известно, как часто природа находится в состоянии П_i. То есть известно распределение вероятностей

p(П_i)=(p₁, p₂, … , p_m).

Такая запись означает, что природа принимает состояние П₁ с вероятностью p₁, состояние П₂ – с вероятностью p₂ и т.д. В этом случае говорят, что решение принимается в условиях частичной неопределенности.

Средние потери в том случае, если статистик использует чистую стратегию B_j определяются по обычной формуле математического ожидания

.

Наилучшей стратегией для статистика, по критерию Байеса, будет стратегия В_j^*, при которой средние потери R_j минимальны.

.

Пример. Пусть в задаче о замене оборудования известны вероятности состояний П_i.

Пi	рi	Вj
		В1	В2	В3
П1	0,2	1	3	5
П2	0,5	5	2	4
П3	0,3	7	6	3

Вычислим средние потери статистика при использовании им стратегий В₁, В₂, В₃:

R₁ = 10,2+50,5+70,3 = 4,8;

R₂ = 30,2+20,5+60,3 = 3,4;

R₃ = 50,2+40,5+30,3 = 3,9.

То есть по критерию Байеса статистик должен выбрать стратегию В₂, в которой средние потери равны 3,4.