
Тема 25
.doc
25. Элементы математической теории оптимального управления
25.1. Постановка задачи оптимального управления экономической системой
В отличии от метода динамического программирования, в теории управления экономическими процессами управление осуществляется непрерывно.
Критерии оптимальности управления обычно связаны либо с получением наибольшей прибыли, либо с достижением минимальных экономических затрат, либо с обеспечением минимального времени процесса. Самым распространенным на практике является критерий минимальных экономических затрат.
Пусть исследуемый экономический процесс, подлежащий управлению, представляет собой перепрофилирование производства, организацию дополнительных цехов, предприятий и т.д. с целью увеличения выпуска продукции. Обозначим y(t) - объем выпускаемой продукции в единицу времени, который естественно будет изменяться во времени t при перепрофилировании производства.
Пусть далее функция u(t) характеризует управление экономическим процессом. Она может представлять собой текущие инвестиции в процесс перепрофилирования, количество рабочей силы, направляемой для этой цели в момент времени t, число единиц специальной техники и т.п. Ясно, что вид функции y(t) зависит от того, какой будет выбрана функция u(t).
Кроме того, очевидно, что в каждый момент времени t текущие экономические затраты g будут зависеть от вида функций y(t) и u(t), т.е.
g = g(y(t), u(t), t).
Чтобы найти полные экономические затраты нужно проинтегрировать g в пределах от момента начала исследуемого процесса t0 до момента его окончания tk. Тогда критерием оптимальности управления является минимизация интеграла
 ,
,
где управление u(t) принадлежит некоторому классу U возможных функций, а y(t) определяется начальным состоянием системы и видом управления, т.е. видом функции u(t).
Определенный интеграл в правой части равенства является числом, которое зависит от выбора функции u(t). Если каждой функции из некоторого множества функций поставлено в соответствие определенное число, то говорят, что задан функционал. В приведенном выше интеграле J(y(t), u(t)) является функционалом.
Как правило, скорость увеличения объема продукции при перепрофилировании производства является функцией вида управления и самого объема производства. То есть имеет место дифференциальное уравнение:
![]() ,
,
здесь производная по времени обозначена точкой.
Кроме того, естественно, известно состояние экономической системы (объем производства) в начальный момент:
y(t0) = y0
и задано состояние системы в конечный момент (т.е. объем производства, на который производство должно быть перепрофилировано в момент окончания процесса):
y(tk) = yk.
Таким образом математически задача оптимального управления экономической системой может быть поставлена следующим образом:
Требуется определить функции u(t) и y(t), минимизирующие функционал
При
этом y(tk)
= yk
,
а функции y(t)
и u(t)
связаны дифференциальным уравнением
![]() с начальным условием y(t0)
= y0.
В этом случае функция
u(t)
называется оптимальным управлением
и обозначается u*(t),
а y(t)
называется функцией оптимальных
параметров производства и обозначается
y*(t).
с начальным условием y(t0)
= y0.
В этом случае функция
u(t)
называется оптимальным управлением
и обозначается u*(t),
а y(t)
называется функцией оптимальных
параметров производства и обозначается
y*(t).
Следует отметить, что в литературе обычно рассматривается более общий случай, когда экономическая система характеризуется не одной переменной (в нашем случае объем производства), а несколькими. При этом управление также включает ряд управляющих параметров. В этом случае y и u представляют собой вектор-функции: y(t) = (y1(t), y2(t), … yn(t)); u(t) = (u1(t), u2(t), … um(t)). Мы же рассматриваем простейший случай n = m = 1.
Поставленная выше задача называется задачей Лагранжа. Принцип оптимальности Лагранжа, согласно которому отыскивается вид оптимальной функции управления, является развитием задачи нахождения условного и безусловного экстремумов.
Рассмотрим алгоритм решения задачи Лагранжа.
-
Составляется функция Лагранжа. Очень часто эту функцию называют - функционалом:
![]() .
.
-
Составляется функция Гамильтона (гамильтониан) H, которая учитывает скорости изменения рассматриваемых функций:
![]() ,
,
где
![]() - неизвестная функция времени, которая
называется неопределенным множителем.
- неизвестная функция времени, которая
называется неопределенным множителем.
Доказана
следующая теорема: Пусть гамильтониан
H(![]() ,
y,
u,
t)
дифференцируем по u,
существует его экстремум в точке u*
и соответствующая функция y*(t)
является оптимальной, т.е. дает экстремум
гамильтониану H
. Тогда можно найти такое оптимальное
значение *
и оптимальную функцию
,
y,
u,
t)
дифференцируем по u,
существует его экстремум в точке u*
и соответствующая функция y*(t)
является оптимальной, т.е. дает экстремум
гамильтониану H
. Тогда можно найти такое оптимальное
значение *
и оптимальную функцию
![]() ,
что экстремум гамильтониана H
совпадет с минимальным значением
функционала J(y,u).
Иначе говоря, у этих функционала и
гамильтониана оптимальный вид функций
,
что экстремум гамильтониана H
совпадет с минимальным значением
функционала J(y,u).
Иначе говоря, у этих функционала и
гамильтониана оптимальный вид функций
![]() y*(t)
и
u*(t)
совпадает.
y*(t)
и
u*(t)
совпадает.
В соответствии с этой теоремой можно получить следующие необходимые условия экстремума:
![]() и
и
![]() .
.
Решение
системы из этих двух уравнений
позволяет получить оптимальную функцию
управления u*(t).
При этом по условиям задачи Лагранжа
начальное условие для
![]() неизвестно. Обычно задается лишь
конечное условие в виде
неизвестно. Обычно задается лишь
конечное условие в виде
![]() .
.
Пример. Задана некоторая система, процесс функционирования которой описывается дифференциальным уравнением
![]() ,
,
определяющим скорость изменения его основной характеристики y = y(t) в зависимости от управления u(t).
Известны начальное и конечное состояния системы: t0 = 0; tk=1; y(t0) = 0, y(tk) = 1. Найти оптимальное управление u* и соответствующую ему функцию y*, которые доставляют минимальное значение функционалу
![]()
Решение.
По
условию задачи
![]() и g(y,u,t)
= u2
+ y.
Составим -функционал
и гамильтониан:
и g(y,u,t)
= u2
+ y.
Составим -функционал
и гамильтониан:
![]()
![]() ;
;
![]() .
.
Для вычисления неопределенного множителя (t) продифференцируем гамильтониан по u и приравняем к нулю. Имеем
![]() .
.
Откуда
![]() .
.
Далее
![]() ,
,
откуда
![]() .
.
Так как по конечному условию
![]() ,
,
то
![]() .
Отсюда
.
Отсюда
![]() .
.
Таким образом, оптимальная зависимость неопределенного множителя *(t) будет иметь вид:
![]() .
.
В
последнем выражении неизвестным является
*.
Для его нахождения воспользуемся
исходным дифференциальным уравнением
![]() .
Подставляя в это уравнение
.
Подставляя в это уравнение
![]()
и интегрируя, получим
![]() .
.
Воспользовавшись начальным условием y(0)=0, получим C1=0.
Таким образом, имеем оптимальную функцию производства:
![]() .
.
Подставляя
в это выражение конечное условие y(1)=1,
вычисляем
![]() .
Окончательно, оптимальная функция будет
иметь вид:
.
Окончательно, оптимальная функция будет
иметь вид:
![]() ,
,
а оптимальная функция управления:
![]() .
.
Минимальное значение функционала J(y, u) равно:
![]()
![]()
![]() .
.
25.2. Принцип максимума Понтрягина
При решении задачи Лагранжа или задачи оптимального управления предполагалось, что управление носит неограниченный характер. На практике управление всегда ограничено по величине. Это ограничение связано с конечным значением возможностей управления.
Пусть ограничение на управление имеет вид, изображенный на рис.25.1.
По задаче Лагранжа

![]()




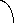
450


- umax 0 +umax u



Рис. 25.1. Реальный и идеальный случаи управления
Тогда
в место управления u
необходимо
использовать, как показано на рис.25.1,
нелинейную функцию
![]() ,
которая будет являться аргументом
функционала Гамильтона. При такой
нелинейности дифференцировать
гамильтониан нельзя.
,
которая будет являться аргументом
функционала Гамильтона. При такой
нелинейности дифференцировать
гамильтониан нельзя.
Впервые
задачу Лагранжа с ограничением решила
группа ученых под руководством академика
Л.С. Понтрягина. Решение задачи явилось
обобщением принципа Лагранжа.![]()
Запишем формулировку задачи принципа максимума Понтрягина: дан объект управления, модель которого описывается дифференциальным уравнением
![]() =
=![]() .
.
Даны начальные условия y(t0)=y0 и заданы ограничения. Рассмотрим два ограничения
q1 (yk)= 0;
q2 (yk)= 0.
Аналогично даны ограничения по скорости изменения функций
![]() =
=
![]() ;
;
![]() =
=
![]() .
.
В отличие от предыдущей задачи добавляется еще ограничения на функцию управления
![]() ;
;
![]() .
.
Необходимо определить оптимальный вид функций y* и u*, которые обеспечивают минимальное значение целевой функции I(y*, u*) при выполнении всех перечисленных выше ограничений. Т.е.
I(y,u)=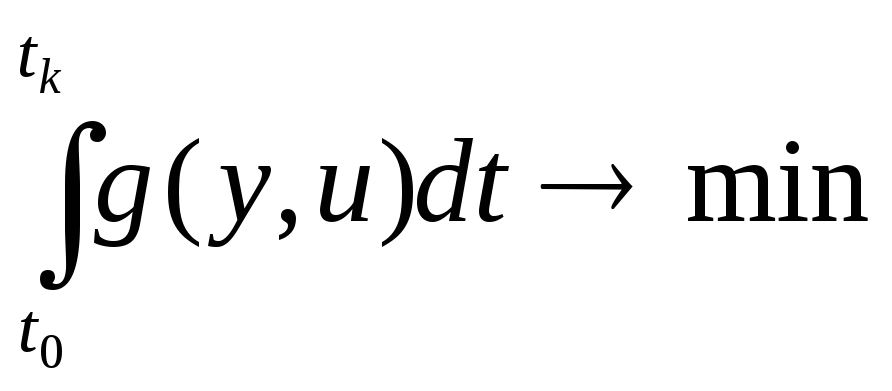 .
.
При решении, аналогично задаче Лагранжа, составляются функционалы Лагранжа и Гамильтона:
![]() =
I(y,
u)+
=
I(y,
u)+![]() q1[yk]+
q1[yk]+
![]() q2[yk],
q2[yk],
H=![]()
![]()
![]() +
+![]()
![]() - g(y,u).
- g(y,u).
Далее воспользуемся теоремой, которую называют принципом максимума Понтрягина:
Если
при оптимальных функциях y*
и
u*существует
минимальное значение целевой функции
I(y*,
u*)
при
выполнении всех перечисленных выше
ограничений, то тогда можно найти такие
оптимальные функции
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
при которых функционал Гамильтона
принимает максимальное значение, т.е.
,
при которых функционал Гамильтона
принимает максимальное значение, т.е.
![]() .
.
Заметим, что в последнем выражении для нахождения управляющей функции u* не производится дифференцирование гамильтониана, а ее значение отыскивается путем перебора.
Сделаем несколько замечаний:
-
Постановка задачи Понтрягина отличается от задачи Лагранжа тем, что включается дополнительное ограничение на управление.
-
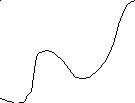
Принцип максимума позволяет найти максимум функционалов на концах отрезка, как это изображено на рис. 25.2, т.к. он не требует дифференцирования гамильтониана.
 H
H



- umax 0 +umax u
Рис.25.2. Вид функционала Гамильтона на отрезке
При этом, если управление u невелико и концентрируется на небольшом отрезке, не достигая границ ограничения, то принцип Понтрягина сводится к решению задачи Лагранжа. Если управление выходит на границу отрезка, то задача решается в постановке Понтрягина и максимум гамильтониана отыскивается путем простой подстановки.
Пример.
Дана система, описываемая уравнением
![]() .
.
Известно
начальное условие y(0)=0
и ограничение
![]() .
Найти оптимальное управление
.
Найти оптимальное управление
![]() и соответствующую ему функцию
и соответствующую ему функцию![]() ,
которые доставляют минимальное значение
целевой функции
,
которые доставляют минимальное значение
целевой функции
I(y,u)=![]() min.
min.
Заметим,
что в условии примера управляющая
функция не входит в подынтегральную
функцию. Кроме того, отсутствуют
ограничения на конечное условие q
и скорость изменения функции
![]() .
Легко убедиться, что в этом случае
функционал Лагранжа совпадает с целевой
функцией I(y,u).
.
Легко убедиться, что в этом случае
функционал Лагранжа совпадает с целевой
функцией I(y,u).
Решение.
Приведем к постановке задачи Понтрягина.
Для этого обозначим
![]() и запишем гамильтониан в виде
и запишем гамильтониан в виде
H=![]()
![]() u
- y.
u
- y.
Применим к последнему выражению принцип Понтрягина
![]() (
(![]() u
- y)
при ограничении
u
- y)
при ограничении![]() .
.
Выражение в скобках состоит из двух слагаемых, из которых второе не зависит от u. Тогда
![]() (
(![]() u
- y)
=
u
- y)
=
![]()
![]() u
при
u
при
![]() .
.
Следовательно,
![]() .
.
По определению
![]() .
.
Интегрируя, получим
![]() .
.
Для вычисления постоянной воспользуемся соотношением
![]() ,
,
но
![]() - функционал в условии задачи не зависит
от y(tk).
Поэтому полагаем
- функционал в условии задачи не зависит
от y(tk).
Поэтому полагаем
![]() =0.
=0.
Кроме того, по условию задачи tk =4, тогда
![]() .
.
Откуда C1=-4. Следовательно
![]() .
.
Построим эту функцию
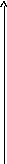
![]()









0 4 t
-4
Рис.25.3. График функции неопределенного множителя
Из
рис.25.3 видно, что на отрезке [0,4], на
котором производится минимизация
целевой функции I(y,u)
, множитель
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Подставив это значение в исходное
дифференциальное уравнение, найдем
.
Подставив это значение в исходное
дифференциальное уравнение, найдем
![]() .
Интегрируя последнюю формулу, находим
.
Интегрируя последнюю формулу, находим
![]() .
С учетом начального условия
.
С учетом начального условия
![]() получим
получим
![]() .
.
Тогда
I(![]() )=
)=![]() .
.
При любом другом управлении меньшее значение получить нельзя.
Пример.
Найти оптимальное управление в системе, описываемой уравнением
![]() .
.
Дано
начальное условие y(0)=0
и ограничение
![]() .
Найти оптимальное управление
.
Найти оптимальное управление
![]() и соответствующую ему функцию
и соответствующую ему функцию![]() ,
которые доставляют минимальное значение
целевой функции
,
которые доставляют минимальное значение
целевой функции
I(y,u)=![]() min.
min.
Решение. Так как ограничения на конечные значения отсутствуют, то
![]() I(y,u).
I(y,u).
Обозначим
![]() и составим
гамильтониан
и составим
гамильтониан
H=![]() u
- (u2
+ y).
u
- (u2
+ y).
Применим принцип Понтрягина
![]() (
(![]() u
- y
– u2)
при ограничении
u
- y
– u2)
при ограничении![]() .
.
Рассмотрим
в начале интервал![]() .
.
Необходимое условие экстремума дает
![]()
![]() –2
u=0.
–2
u=0.
Откуда
![]() при
при
![]() .
.
Для
вычисления
![]() воспользуемся
воспользуемся
![]() .
.
Аналогично вычислениям в примере 2 получаем
![]() .
.
Вид этой функции показан на рис.19.3 . Подставляя полученную функцию в выражение для u, получим
![]() .
.
Но
![]() ,
тогда
,
тогда
![]() .
Откуда 2 < t
< 6.
.
Откуда 2 < t
< 6.
По
условию задачи правый конец интервала
![]() =4,
поэтому принимаем
=4,
поэтому принимаем
2
< t
![]() 4.
4.
Теперь
рассмотрим случай, когда
![]() .
В соответствии с проведенными вычислениями
и рис.19.3 этот случай может быть только
на отрезке 0
.
В соответствии с проведенными вычислениями
и рис.19.3 этот случай может быть только
на отрезке 0
![]() t
t
![]() 2. Аналогично вычислениям в примере 2
2. Аналогично вычислениям в примере 2
![]() .
.
Из
рис.19.3 видно, что на отрезке [0,2], на
котором производится минимизация
целевой функции I(y,u)
, множитель
![]() .
Тогда
.
Тогда
![]() .
.
Таким образом, управляющая функция будет иметь вид
![]()
Тогда, подставляя управляющую функцию в исходное уравнение, оптимальная система с точки зрения заданного критерия и ограничений будет описываться дифференциальным уравнением
![]()
На рис.25.4 показаны полученные функции.

![]()
![]()
