26. Математические игры

26.1. Игра как модель конфликтной ситуации

Часто необходимо принимать решения в ситуациях, когда две или более сторон преследуют противоположные цели. Каждая из сторон может проводить мероприятия для достижения своих целей, причем успех одной стороны означает неудачу других. Такие ситуации называются конфликтными, они могут возникать, например, при игре в шахматы, в домино и т.д.

В экономике к конфликтным ситуациям относятся взаимоотношения, например, между:

- поставщиком и потребителем;

- покупателем и продавцом;

- банком и клиентом;

- конкурирующими фирмами и т.д.

Примерами конфликтных ситуаций являются спортивные соревнования, арбитражные споры, выборы.

Методы решения задач с конфликтными ситуациями разработаны математической теорией конфликтных ситуаций, которая получила название «теория игр». Чтобы сделать возможным математический анализ конфликтной ситуации, ее необходимо упростить, учтя только основные факторы.

Основные понятия теории игр:

игра – упрощенная формализованная математическая модель конфликтной ситуации;

игроки – стороны, участвующие в конфликте;

выигрыш (проигрыш) – исход конфликта;

правила игры – систему условий, определяющих:

- варианты возможных действий игроков;

- величину выигрыша (проигрыша), к которому приводит каждая совокупность действий игроков;

- объем информации о поведении других игроков и т.п.

Игра называется парной, если в ней участвуют два игрока и множественной, если большее число игроков. Игра называется игрой с нулевой суммой (антагонистической), если суммарный выигрыш одних игроков в точности равен суммарному проигрышу других.

Рассмотрим сначала парные игры с нулевой суммой, в которых участвуют игроки А и В. При этом договоримся о следующей терминологии. Будем считать, что результат любой такой игры выражается некоторым числом (допустим, денежных единиц), которое назовем выигрышем игрока А и обозначим его a. Если игрок А в данной игре проиграл, то a – отрицательное число, но все равно будем называть его выигрышем. Тогда то же самое число a – проигрыш игрока В; если игрок В выиграл, то это число, естественно, отрицательное.

Назовем стратегией игрока совокупность его действий в процессе одной игры. Будем считать, что в данной игре все решения каждым игроком приняты заранее, независимо от действий другого игрока. При этом в распоряжении каждого игрока имеется не одна (иначе отсутствует смысл игры), а несколько или даже бесконечное множество стратегий, из которых в данной игре он выбирает одну.

Игра называется конечной, если у каждого игрока конечное число стратегий, и бесконечной в противном случае. Очевидно, что если каждый игрок выбрал свою стратегию, то исход игры определен.

Под решением игры будем понимать пару стратегий по одной для каждого игрока, при которых игрок А должен получить максимальный выигрыш, если игрок В придерживается свой стратегии, а игрок В должен иметь минимальный проигрыш, если игрок А придерживается своей стратегии. Такие стратегии, составляющие решение игры, называются оптимальными. Оптимальные стратегии должны удовлетворять условию устойчивости, т.е. любому игроку должно быть невыгодно отказываться от своей оптимальной стратегии, если другой игрок придерживается своей оптимальной стратегии.

Главной задачей теории игр является отыскание решения игры, т.е. выбор оптимальных стратегий для каждого игрока.

26.2. Матричные игры

Рассмотрим парную конечную игру с нулевой суммой. Пусть игрок А располагает m стратегиями A₁, A₂, … A_m, а игрок В располагает n стратегиями B₁, B₂, … B_n. В результате выбора игроками какой-либо пары стратегий A_i и B_j однозначно определяется результат игры a_ij, который является выигрышем игрока А (положительным или отрицательным) и одновременно проигрышем игрока В.

Предположим, что значения a_ij известны для любой пары стратегий игроков, и тогда их можно записать в форме матрицы. Матрица Q = (a_ij)_mn называется матрицей игры (в некоторых книгах – платежной матрицей или матрицей потерь), а сама игра в этом случае обычно называется матричной игрой. Строки матрицы соответствуют стратегиям игрока А, а столбцы – стратегиям игрока В. Для наглядности такую матрицу часто пишут в виде таблицы:

Bj Ai	B1	B2	…	Bn
A1	a11	a12	…	a1n
A2	a21	a22	…	a2n
…	…	…	…	…
Am	am1	am2	…	amn

Игрок А стремится обеспечить себе наибольший выигрыш, т.е. выбрать стратегию A_i так, чтобы величина a_ij была максимальной. Игрок В стремится сделать свой проигрыш наименьшим, т.е., чтобы a_ij была минимальной. Таким образом, цели игроков являются прямо противоположными.

Определение наиболее рационального способа ведения игры для каждого из игроков и представляет собой существо теории игр.

Пример. Игрок А может спрятаться в одном из двух убежищ: I и II. Игрок В называет убежище, в котором, по его мнению, спрятался игрок А и, если угадывает, то получает от А одну денежную единицу, а если не угадывает, то платит А столько же. Составить матрицу игры.

Решение.

Обозначим стратегии игроков:

А₁ – игрок А спрятался в убежище I.

А₂ – игрок А спрятался в убежище II.

В₁ – игрок В называет убежище I.

В₂ – игрок В называет убежище II.

Тогда матрица игры имеет вид:

.

26.3. Цены и оптимальные стратегии игр

Рассмотрим матричную игру со следующей матрицей:

.

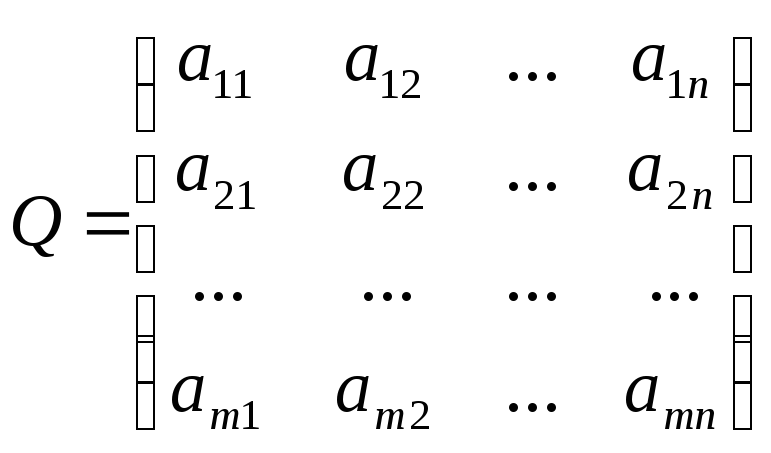Обозначим _i – наименьший выигрыш игрока А при выборе им стратегии A_i при всех возможных стратегиях игрока В. Тогда _i является наименьшим числом в i-той строке матрицы игры, т.е.

.

Обозначим _j – наибольший проигрыш игрока В при выборе им стратегии B_j при всех возможных стратегиях игрока A В этом случае _j - наибольшее число в j-том столбце матрицы игры, т.е.

.

Среди всех чисел _i выберем наибольшее, обозначим его  и назовем нижней ценой игры или максимином. То есть,

.

Это гарантированный наименьший выигрыш игрока А при выборе им стратегии, соответствующей  и при любой стратегии игрока В. Стратегия игрока А, соответствующая максимину, называется максиминной стратегией.

Среди всех чисел _j выберем наименьшее, обозначим его  и назовем верхней ценой игры или минимаксом. То есть,

.

Это гарантированный наибольший проигрыш игрока В при выборе им стратегии, соответствующей  и при любой стратегии игрока А. Стратегия игрока В, соответствующая минимаксу, называется минимаксной стратегией.

Можно доказать, что нижняя цена игры не превосходит верхней цены игры, т.е.   . Очевидно, что максиминная и минимаксная стратегии – наиболее осторожные стратегии игроков. Принцип, диктующий игрокам выбор таких стратегий, называется принципом минимакса.

Если  = , то число c =  =  называется чистой ценой игры или просто ценой игры. Максиминная и минимаксная стратегии в этом случае являются оптимальными стратегиями, а их совокупность – решением игры. Действительно, т.к. число c =  является наибольшим в своем столбце, то игроку А невыгодно отказываться от максиминной стратегии (т.е. передвигаться вверх или вниз по этому столбцу), если игрок В придерживается минимаксной стратегии. Аналогично поскольку число c =  является наименьшим в своей строке, то игроку В невыгодно отказываться от минимаксной стратегии, если игрок А придерживается максиминной.

Из вышесказанного следует, что пара стратегий A_i и B_j дает решение игры тогда и только тогда, когда соответствующий ей элемент a_ij является одновременно наименьшим в своей строке и наибольшим в своем столбце.

Если в игре существует такая ситуация, то указанный элемент a_ij называется седловой точкой, а сама игра – игрой с седловой точкой (по аналогии с поверхностью седла, которая искривляется вверх в одном направлении и вниз – в другом). Игра с седловой точкой имеет цену игры с = a_ij. Игра с седловой точкой называется справедливой, если c = 0 и несправедливой в противном случае.

Пример. Определить нижнюю и верхнюю цену игры, заданной матрицей:

.

Имеет ли игра седловую точку. Если да, то найти решение игры.

Решение.

Найдем  и , заполнив для удобства следующую таблицу:

В А	В1	В2	B3	i
A1	0,5	0,6	0,8	0,5
A2	0,9	0,7	0,8	0,7
A3	0,7	0,6	0,6	0,6
j	0,9	0,7	0,8	 =  = 0,7

Из таблицы видно, что максиминная стратегия – стратегия A₂ и соответствует значению  = 0,7, а минимаксная стратегия - стратегия В₂, соответствующая  = 0,7. Так как  = , то элемент a₂₂, находящийся на пересечении второй строки и второго столбца является седловой точкой. Пара стратегий (A₂, B₂) составляет решение игры, поскольку при  =  максиминная и минимаксная стратегии являются оптимальными. Цена игры с =  =  = 0,7.