26.4. Смешанные стратегии

Если   , то игра не имеет седловой точки и возникают затруднения в определении цены игры и оптимальных стратегий игроков. Рассмотрим в качестве примера такую игру.

Пример. Игроки А и В одновременно независимо друг от друга записывают число. Игрок А записывает 1 или 2, а игрок В записывает 0 или 3. Если сумма записанных чисел нечетна, то столько денежных единиц игрок В платит игроку А, а если сумма четна, то столько А платит В.

Решение.

Обозначим стратегии:

A₁ – игрок А записал 1; А₂ – игрок А записал 2;

В₁ – игрок В записал 0; В₂ – игрок В записал 3.

Матрица игры имеет вид:

.

Найдем  и , для чего заполним таблицу:

В А	В1	В2	i
А1	1	-4	-4
А2	-2	5	-2
j	1	5	=-2 =1

Т.к.   , то ясно, что седловая точка в этой игре отсутствует. Из таблицы видно, что при максиминной стратегии А₂ игрок А может гарантировать себе выигрыш не меньше -2, а игрок В при минимаксной стратегии В₁ может гарантировать себе проигрыш не больше 1. Область между  и  является как бы ничейной, и каждый игрок может попытаться улучшить свой результат за счет этой области.

Отметим, что если каждый игрок будет придерживаться принципа минимакса (стратегии А₂ и В₁), то каждый раз выигрыш игрока А будет составлять - 2. Это невыгодно игроку А, т.к. проигрыш игрока В, равный - 2 (т.е. выигрыш 2), меньше того проигрыша, равного 1, который игрок В обеспечивает себе по принципу минимакса.

Игроку А выгодно отказаться от своей максиминной стратегии, если В придерживается минимаксной и применить стратегию А₁. Тогда игрок А вместо выигрыша - 2 получит выигрыш 1. Правда, тогда игроку В будет выгодно отказаться от стратегии В₁, чтобы игрок А получил выигрыш - 4 и т.д. То есть, при каждой паре стратегий одному из игроков выгодно отказаться от своей стратегии, если другой игрок придерживается своей. А это значит, что пары оптимальных стратегий нет и решение игры не существует.

Ясно, что в такой игре каждый игрок должен хранить в секрете ту стратегию, которую он собирается применить. Однако как это сделать? Ведь если партия играется многократно, а один из игроков все время применяет одну и ту же стратегию, то второй об этом знает.

Секретность можно сохранить, если каждый раз выбирать стратегию случайным образом. Такое поведение тоже является стратегией и называется смешанной стратегией в отличие от рассмотренных ранее чистых стратегий А₁, А₂, … А_m, В₁, В₂, … В_n. При этом другая сторона лишена возможности узнать наперед о действиях другой стороны.

Итак, смешанная стратегия S_A игрока А – это применение чистых стратегий А₁, А₂, … А_m случайным образом с вероятностями соответственно p₁, p₂, … p_m, причем

.

Смешанную стратегию S_A обычно записывают в виде вектора вероятностей:

S_A = (p₁, p₂, … p_m).

Аналогично смешанная стратегия игрока В:

S_B = (q₁, q₂, … q_n),

где q_j – вероятность применения игроком В стратегии B_j, а .

Поскольку в смешанных стратегиях игроки выбирают свои чистые стратегии случайным образом и независимо друг от друга, игра имеет случайный характер. Случайной становится и величина выигрыша игрока А (или что то же самое проигрыша игрока В). В этом случае представление о том, какому игроку выгодна данная игра при выбранных смешанных стратегиях игроков, дает среднее значение выигрыша игрока А, которое является функцией S_A и S_B и определяется по формуле математического ожидания двумерной случайной величины:

.

Эту функцию часто называют функцией потерь или платежной функцией.

Решением игры в этом случае является пара оптимальных смешанных стратегий

S_A^* = (p₁^*, p₂^*, … p_m^*) и S_B^* = (q₁^*, q₂^*, … q_n^*),

обладающих тем же свойством, что и для чистых стратегий: каждому игроку невыгодно отступать от своей оптимальной смешанной стратегии, если другой игрок придерживается своей оптимальной смешанной стратегии.

Ценой игры c в такой игре называется средний выигрыш игрока А при оптимальных смешанных стратегиях:

.

Цена игры с удовлетворяет неравенству   с  , где  и  - соответственно нижняя и верхняя цена игры.

Справедлива следующая основная теорема теории игр – теорема Неймана: Каждая конечная игра имеет, по крайней мере, одно решение среди смешанных стратегий.

Рассмотрим игру с матрицей , являющуюся простейшим случаем матричной игры. Если такая игра имеет седловую точку, то решение игры – пара оптимальных чистых стратегий (максиминная и минимаксная), соответствующих этой точке. Для игры, в которой отсутствует седловая точка, решение в соответствии с теоремой Неймана существует и определяется парой оптимальных смешанных стратегий:

S_A^* = (p₁^*, p₂^* ) и S_B^* = (q₁^*, q₂^* ).

Пусть матрица игры имеет вид:

.

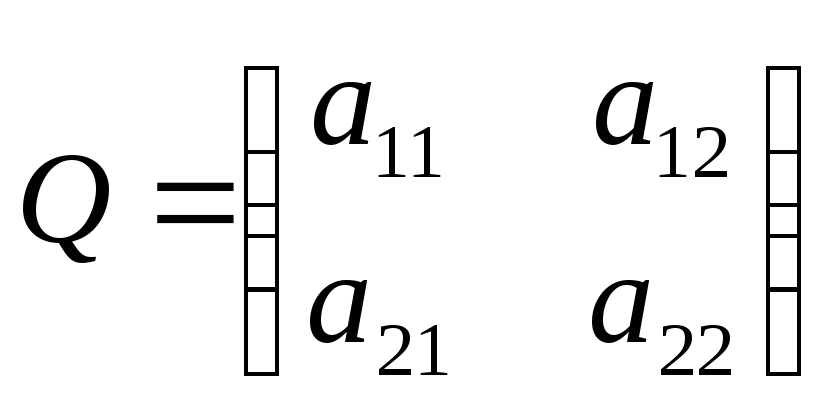Рассматривая функцию потерь f(S_A, S_B) при применении смешанных стратегий, можно получить систему уравнений для нахождения оптимальных смешанных стратегий, решение которой имеет вид:

; ;

; .

Пример. Найти решение и цену игры для описанной ранее игры с записью чисел.

Решение.

Полученная ранее матрица игры имеет вид:

.

Решение игры определяется следующими вероятностями:

;

;

;

.

Таким образом, ; .

Полученный результат означает, что оптимальная смешанная стратегия игрока А состоит в том, чтобы применять чистые стратегии A₁ и A₂ случайным образом с вероятностями соответственно и , а игрока В – чистые стратегии В₁ и В₂ – с вероятностями и . Найдем цену игры с, т.е. средний выигрыш игрока А при оптимальных смешанных стратегиях:

.

Цена игры, т.е. средний выигрыш игрока А, отрицательна. Следовательно, эта игра для игрока А невыгодна, а выгодна для игрока В.