
Tulenko Двойные интегралы
.pdfВЫСШЕФЕДЕМИНИСТЕАЛЬНОЕОБО ПАЗÑÒÂÎОФЕВАТЕЛЬОСУДАÑÓÄÀÑÈÎÎÁ ÀÇÎСТВЕННЫЙОЕСТАЛЬНОУЧЕННОЕÈßЕЖДЕНИЕО ОББЮДЖЕТНОЕНАУКИАЗОВАНИЯÔ
¾ВО ОНЕЖСКИЙ О УНИВЕ СИТЕТ¿
Е. Б. Туленко
СВ ЙСТВАД ОЙНОЙ ИНТЕ АЛ, ÅÏÎ ИЛОЖЕНИЯИ СПОСОБЫ ВЫЧИСЛЕНИЯ.
К ЕОМЕТ ИИ ФИЗИКЕ
Учебно-методическое пособие для вузов
Издательско-полигра ический центр Воронежского г сударственного университета 2012
Утверждено научно-методическим советом изического акультета 05 июня 2012 г., пр токол • 6
ецензент д-р из.-мат. наук, доц. ка едры теоретической изики А. С. Корнев
Учебно-методическое пособие подготовлено на |
а едре м тематичес- |
|||
кой из ки изического акультета Воронежсêого госудàрственного |
||||
университета. |
|
|
|
|
екомендуется для студентов 1-го 2-го курсов изического акуль- |
||||
тета дневной вечерней орм обучения. |
|
|
||
140800специальностей:Яд рные изикаполупроводниковыетехнологи |
|
электроника, 010803 |
||
Äëÿ |
|
010801 адио изика |
||
Микроэлектроника |
|
приборы, 010701 |
||
21 1 |
Эл ктроника наноэлектрон ка, 210600 НанотехнологияФизика, |
|||
|
|
2 |
|
|
|
|
|
|
Введение |
|
|
|
Методическое пособие содержит материал по одному из |
|||||
важных разделов курса математического анализа. В нем |
||||||
приведе ы необх димые теоретические сведени , рассм т- |
||||||
ðåíî ïîíÿòèå |
дв йного |
|
|
описываютсÿ |
||
его свойства и способы вычисления. яд пр меров основныеподроб |
||||||
ным описан ем хода решения,интеграла,также индивидуальные за- |
||||||
дания разлèчн й сложности позволят студентам хорошо |
||||||
|
достатîчно сложный материал. Особое |
|||||
ксвоитьк случае |
|
|
системы координат, таквниманиеслу- |
|||
ó |
методу сведения двойного интеграла к повторным |
|||||
чделеноà перехода к крив линейным коор инатам, в частности к |
||||||
ï |
олярной системедекартовойординат. Последний раздел посвящен |
|||||
|
двойного |
интеграла |
решению геометричес |
|||
кихриложениямизических зад ч. Пособие предназначено для изу |
||||||
чения материа |
как на практических занятиях по матема- |
|||||
тическому анализу, так и во время самостоятельной работы |
||||||
студентов. |
1. |
Двойной интеграл |
||||
|
|
|||||
|
|
|
|
|
авнениями,плоскуюимиченает областьконечнымто уютакая,площадьчисломпустьобластькри.эта- |
|
|
|
|
|
ограесть |
D |
|
|
|
|
|
ó |
|
|
квадрируемавых,областьПустьЕслиассмотримзаданныхплоскаяквадрируема,на.областизамкнуявнымиобластьую |
|
|||||
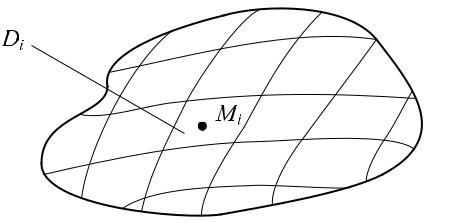
(сеткойобщейтак, чтобычастиониграницыпересекалиськривых) n квадрируемых(рис.1)друг. с |
|
íûõ |
D пределена |
f x, y . азобьемна îбласть D
3
ункция двух переменпроизвольным образом частейдругомDнеi, iболее= 1, 2чем, . . .по, n
|
|
èñ. 1 |
|
|
|
|
Обозначим площадь каждойобластей- части через |
Sрасстоя, наи |
|
||||
больший из диаметров всех |
i |
|
|
|||
æдойу точкамичастиобластиданíойазывается-областих |
.наибольшее. |
i |
|
|
||
ниеВДиаметромка |
|
i |
d |
|
- |
|
цииЭта сумма называетсяσ = |
интегральнойf(ξ , η )ΔS . суммой для унк(1)- |
|||||
Di выберем произвольно точку Mi(ξi, ηi |
|
, |
||||
умножимвычислимнав каждой точке значение ункции f(ξi, ηi) è Si. Построим сумму:
n
|
Xi |
|
i |
|
|
|
|
i i |
|
|
|
|
=1 |
|
|
|
|
тегральнойОпределениеf(x, y) насуммыобласти1. Если(1)Dприсуществует. |
конечный предел ин- |
||||
способа разбиения области |
d →части,0 |
çà èñèò íè îò |
|||
|
обозначаетсяD |
|
|
ни от выбора точек |
|
Mi, òî |
называется двойным интегралом от ункции |
||||
f(x, y) по области D |
|
|
|
|
|
ãäå |
ZDZ |
f(x, y)dS, |
|
|
(2) |
ластиВdSэтомэлементслучае площадиункция называется. |
интегрируемой на об- |
||||
D. |
|
4 |
|
|
|
двойнойВ декаринтеграловой системеможем записатькоординатв видеdS = dxdy, поэтому
ZZ
Основные свойства двойногоf(x, y)dxdyинтеграла:.
D
òî 1o.ункцияЕсли ункции f(x, y) è g(x, y) интегрируемы на D причем f(x, y) + g(x, y) интегрируема на области D,
ZZ
(f(x, y) + g(x, y))dxdy =
D |
|
|
= ZDZ |
f(x, y)dxdy + ZDZ |
g(x, y)dxdy. |
2o. Если ункция f(x, y) интегрируема на D, то ункция kf(x, y), ãäå k = const интегрируема на области D, причем
ZZ ZZ
kf(x, y)dxdy = k f(x, y)dxdy.
D D
o |
|
|
|
|
|
ëà 3ть. Пустьсостоит ункцияиздвухfквадрируемых(x, y) интегрируемаобластейнаDтогда,сама об |
|||||
ресекающихся только |
по общей части гран цы, D1 |
è |
D2 |
||
öèÿ |
|
|
|
|
óíê,ïå- |
f(x, y) интегрируема по каждой из этèх областей и |
|||||
ZDZ |
ZDZ |
f(x, y)dxdy + |
ZDZ |
|
|
f(x, y)dxdy = |
|
f(x, y)dxdy. |
|||
|
1 |
|
2 |
|
|
5
2. Вычислениедекартовой(сведениедвойногосистемек повторному)координатинтеграла в
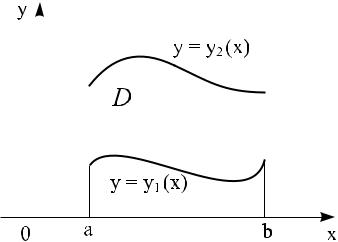
криволинейнуюI.Пустьобластьтрапециюинтегрирсоснованиями,оси D представляетпараллельнымисобой
âûìèOy, а снизу сверху ограниченную непрерывными кри- y = y1(x) è y = y2(x) (ðèñ. 2).
|
|
|
èñ. 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
||||
Такую область интегрирования назовем простой относи- |
|||||
Теоремат льно оси1.OyПусть. |
ункция |
||||
для каждого иксированного f(x, y) интегрируемаинтегралнаD ãðàë x [a, b] существует -
y2(x)
R
f(x, y)dy, тогда существует повторный
y1(x)
by2(x)
ZZ
dx |
f(x, y)dy |
ay1(x)6
и он равен двойному
Òàê |
|
ZDZ f(x, y)dxdy. |
|
|
|
|
минтегрированияобразом,случае простой относительно оси |
|
|||
областè |
справедлива ормула |
Oy |
|||
II. ПустьZZ |
b |
y2(x) |
|
||
f(x, y)dxdy = Za |
dx Z |
f(x, y)dy. |
|
||
|
область интегрирования |
|
(3) |
||
|
D |
|
y1(x) |
|
|
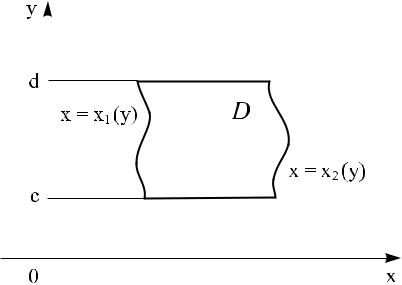
осикриволинейную трапецию с основаниями,D представляетпараллельнымисобой
âûìèOx, а слева справа ограниченную непрерывными кри- x = x1(y) è x = x2(y) (ðèñ. 3).
|
|
èñ. 3 |
|
|
|
Такую область интегрирования назовем простой относи- |
||
Теоремат льно оси2.OxПусть. |
ункция |
|
для каждого иксированного f(x, y) интегрируема на D è 7y [c, d] существует инте-
ãðàë x2(y)
R
f(x, y)dx, тогда существует повторный интеграл
x1(y)
dx2(y)
ZZ
и он равен двойному dy |
f(x, y)dx |
cx1(y)
Таким об азом дляZDZ f(x, y)dxdy. |
îñè |
простой отн сительно |
|
сти интегриðования справедлива ормула |
Ox îáëà- |
d x2(y) |
|
вычисляютсяихралы,Ввычислениякоторыеормулахсправа.отличаются(3)И тойналево,(4)присутствуютдругстоитдругойотестьдругасначалаормулахповторныелишьвычисляетинтегралыпорядком(4) |
|||||||
|
ZZ f x, y)dxdy = Zc |
dy |
Z |
f(x, y)dx. |
-- |
||
|
D |
|
|
x1 y) |
|
|
|
èíò ãðàë, |
|
справа (внутренний интеграл), при |
|||||
ýòîì ïåременна , |
íå |
|
под знаком ди ерен |
||||
циала, считаестоящий |
|
затем |
вычисляетсярезультате |
||||
(внешний) интегралкотораяу кции, |
|
||||||
вычисл |
ия внутреннегопостоянной,теграла,полученнойоставшейся |
второй |
|||||
переменнойЗамечание:. |
нужно помнить, что в силу своего определе- |
||||||
|
й интеграл это число, поэтому пределы интегри- |
||||||
рованиядвойнî внешнем интеграле должны быть всегда посто |
|||||||
янными, |
пределы |
|
интеграла могут зависеть |
||||
отеренциалатой переменной,. котораявнутреннегостоит в нем под знаком ди -
8
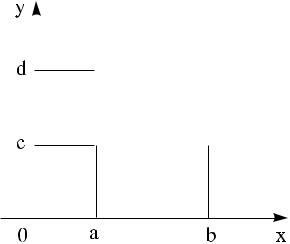
прямоугольнойво внешнем,Пределы интегрированиятакобластиво внутреннеминтегрированиямогутинтегралеáûòü(ðèñпостояннымитолько. 4). в случаеêàê
|
|
|
|
является |
|
|
|
|
|
|
|
|
|
|
|
Åñëè îáëà òü |
|
|
èñ. 4 |
|
|
êàê îò |
|
|
|
||||||
|
|
|
|
|
|
|
- |
íятьодынтегральнойосите(3),я вычислениятакоси интегрированияормулу,ункциитакдвойноготн(4). сВыборèнтегралательноопросиможнопростойделяетсявычислялись,какпримедомор |
|||||||
ìóëó |
Oy |
|
|
|
|
Ox |
|
тегрированиягпрощеированияДалее.будемтак,рассматриватьункциичтобыповторныеf(x,непрерывныеy). Выбираинтегралынапорядокобластиинтеин
прерывна на замкнутойfобласти(x, y), поскольку, если ункция не- |
||
|
|
- |
ыхойейЗамечание:интегралдляункцийормулыинтегрируемости.может(3),условие(4)существоватьимеютнепрерывнункцииместоне.тоЭто.ститолькоонаявляетсяозначает,интегрируемадлянепрерывдостатчтодвîíàé÷ |
||
îìó |
D |
|
Íà |
при сведении двойного интеграла к повтор |
|
íия отпрактикестых, рассмотренных выше. |
|
|
|
уметь отличать сложные области интегрирова- |
|
Длянужноэт го есть относительно простой прием. |
|
|
|
9 |
|

ся простойЧтобы проверот осительноь, чтоосиобласть интегрирования D являет
нения перемеííîé Oy, за иксируем область изме-
каждую точку отрезкаx отрезок [a, b] îñè Ox, проведем через
[a, b] вертикальную прямую (рис. 5).
|
èñ. 5 |
|
|
Если каждая такая прямая пересекает границу области |
|||
Dняянечастиболееописываютсяграницы,чемдвухзаключенныеточках(условиемежду1),апрямыминижняяуравнениемверх- |
|||
условиями: |
|
|
x = a |
x = b, |
каждая одним явным |
||
y = y1(x) |
y = y2(x) соответстве но (условие 2), то область |
||
|
í |
îñè |
определяется |
D является простой относительусловий,Oy |
|
||
|
простойодно изотносительнповторному. бластьоси интегри- |
||
рованияЕслиненевыполняетсяaявляется≤ x ≤ b, y1(x) ≤ y ≤ y2(x) |
|
||
ñразбитьведения1)разуЗамечание:еслипользоватьсянадвойногонепростыевыполняетсяинтеграланельзяпрямыми,.условиепараллельнымик1,тообластьосиормулойOyследуетдля(3) |
|||
6, 2). еслинапростневûполняетсяпрямыми,условиепараллельными2,тобластьосинужноOy (рисраз.
|
- |
ходящими через точки области |
изменяетсяOy ïðî |
10 |
D в которых |
