
Tulenko Двойные интегралы
.pdfZZ ZZ ZZ
нымСначаСведемивычкаждому интегралурассмотримслимнтегралы,внешнегоxydxdyèõ, =применяяотдеинтеграластоящиеобастььностиxydxdyописанныев.правой+ xydxdyчасти,ранее.кприемыповтор(5)к-
D |
D1 |
D2 |
пределяютсяû |
D1 |
переменной |
|
Преде |
|
ïî. |
|
íûå è |
из условия |
|
y постоян |
реннего интеграла з висят от переменной0 ≤ y ≤ 1, пределы нут- |
|||
правая границы |
|
|
левая |
|
области |
|
y, поэтомуграницы |
|
|
|
|
|
|
|
|
|
D1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
и, зависящими от переменнойдолжны описываться урав ени- |
||||||||||||||||||||||||||||||||||||
èìååì |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y. Так, для левой |
|
|
|
x |
|
0 |
|||||||||||||
|
правойx = √y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = x |
2 ïðè |
|
||||||||||||||||||
äëÿ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
), |
|||||||||||||
|
|
|
(обратная ункция для |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≤ïðè |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x = √y (обратная ункция для y = x2 |
|
||||||||||||||||||||||||||||||
x ≥Окончательно0). |
для области |
D1 получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
y |
|
|
1 |
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
y |
|
|
|
|
|
|||||||
ZZ |
|
|
|
|
Z |
|
|
Z |
|
|
Z |
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|||||||||||
D |
|
|
|
|
0 |
|
|
|
√y |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 |
xydxdy = |
dy |
|
|
|
|
|
|
xydx = |
dyy |
|
2 |
|
|
|
√y |
= |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1тавимобластив виде повторногонаправлении,вычислим(6) |
|||||||||||||||||||||||||||||
двойнойА алогично,интегралпред=ïîñ2 Z0 |
y(y − y)dy = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ванного значения |
|
|
|
|
|
|
|
|
|
|
|
D2. Для каждого иксиро- |
||||||||||||||||||||||||
зн че ия от прямойy [1, 4] переменная x может |
|
|
|
|
инимать |
|||||||||||||||||||||||||||||||
указаИмеемном стрелкамиxíà=ðèñy . |
|
.äî x = √ |
|
â |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
4 |
|
|
y |
|
|
4 |
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
||||||||
|
ZZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
y |
|
|
|
|
|||||||||||
|
|
|
|
|
Z |
|
|
|
Z |
|
|
Z |
|
2 |
|
|
|
− |
2 = |
|
|
|||||||||||||||
|
D |
|
|
|
|
1 |
|
|
−2 |
|
|
1 |
|
|
|
|
|
|||||||||||||||||||
|
2 |
xydxdy = |
|
dy |
|
|
|
|
|
xydx21 = |
dyy |
|
y |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|||
1 |
Z y y − (y − 2)2 |
|
|
|
|
|
1 |
Z |
|
5y2 − y3 − 4y dy = |
||||||||||||
= |
|
dy = |
|
|
||||||||||||||||||
2 |
2 |
|||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
4 |
|
|
|
|||
|
|
|
|
|
1 |
|
5y3 |
|
|
y4 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
− 2y2 |
1 = |
|
|
|
||||||||||
|
|
|
|
|
= 2 |
3 − |
4 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
5 |
64 |
|
|
|
|
|
5 |
|
|
|
1 |
|
|
45 |
5 |
|
|||||
(5),Подставлокончат |
ельняя ïîлученныеполучим в (6) è |
|
(7) 2значе= íèÿ=â5 |
ормулу. (7) |
||||||||||||||||||
|
||||||||||||||||||||||
= 2 |
|
·3 |
− 64 − 32 − 3 |
+ |
4 + |
8 |
8 |
|
||||||||||||||
|
|
|
|
|
ZDZ |
|
|
|
|
|
|
|
|
|
|
5 |
5 |
оказалсям способестаноболеере-- |
||||
|
|
|
|
|
xydxdy = 0 + 58 |
= 58. |
|
|
|
|||||||||||||
затруднительнымшения,Замечание:Ответнополучилсявданномиз.рассмотренныхпримеретотже, чтовторои éпривышспопервñîå бпримеров |
||||||||||||||||||||||
вится ясно, что для упрощения вычисл ний |
ряде задач |
|||||||||||||||||||||
нужно уметь св дить двойные интегралы к |
ì ñ |
|||||||||||||||||||||
òåì èëè èíûì ïîрядком интегрирования. Приповторнэтом ûáîð |
||||||||||||||||||||||
определяется как видом |
|
|
|
|
|
|
|
интегрирования, так и ви- |
||||||||||||||
ассмотрим еще одинобластипр мер. |
|
|
|
|
|
|
|
|||||||||||||||
дом интегрируемой ункции. |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Пример 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В двойном интеграле |
RR |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
íиятегралерасставитьограниченатомпредеином- |
|||||
порядке,лы интегрированияеслиобластьв повтоинтегрироваfíîì(x, y)dxdy |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
âûìè: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
êðè- |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
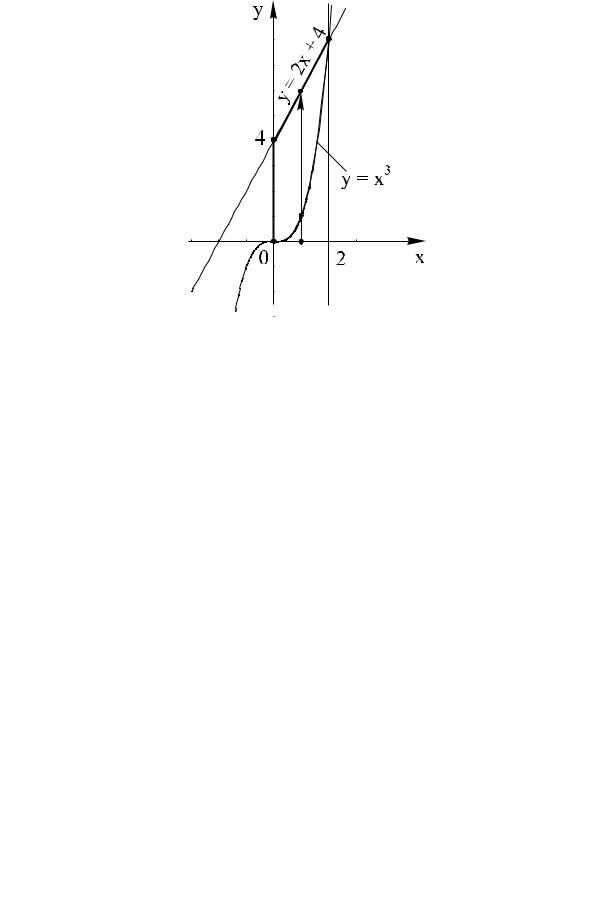
1. Изобразимy = x , x =ãðà0, yически= 2xешение+область4. |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
D (ðèñ. 13). |
||||
|
|
|
|
èñ. 13 |
|
|
|
|
2. Сначала сведем наш интеграл к повторному вида |
||||||||
|
|
|
b |
y2(x) |
|
|
|
|
Äëÿ |
|
|
иксируем область изме |
ния переменной |
||||
|
этого за |
Za |
dx Z |
f(x, y)dy. |
|
|||
|
|
|
|
y1(x) |
|
|
|
|
xнашем(по нейпримере:идетинтегрирование во внешíем интеграле), в |
||||||||
буюКаждаяточкуотрезкавертикальная0 ≤ x ≤ 2.прямая, проходящ я через лю- |
||||||||
3 |
|
|
[0, 2] îñè Ox пересекает сначала кривую |
|||||
àтемпраотносительнокривуюлении |
|
при движении в положи- |
||||||
yòå=üíîìx , ровноз |
â äâóõ |
y = 2x + 4 |
|
|
|
|||
ëастипростой |
чкахоси.Следовательно,тоестьпересекаетобластьграницуявля- |
|||||||
обется |
|
|
|
Oy |
|
|
|
|
ременнаяДлянужновсех. внутренних точек областиразбиватьинтегрированияееначастипе- |
||||||||
íå |
|
|
|
|
Oy |
|
|
|
до прямойy будет изме яться от уравнения кривой y = x3 |
||||||||
|
y = 2x + 4 (направление23 |
указано на рис. 13). |
||||||
В результате получим
ZZ |
|
2 |
|
2x+4 |
|
f(x, y)dxdy = |
Z0 |
dx |
Z3 |
f(x, y)dy. |
|
повторного,переменной3.интегралТеперьпредставимбудемдругимвычислятьисходныйпорядкомпеременнойдвойнойинтегрированияинтегралвнутрен.Внешвиде |
|||||
D |
|
|
|
x |
|
íèé |
|
x, |
- |
Для этого за иксируемy. |
область измен |
переменной |
|
прямымиестьy длявсевсехвозможныеточекобласти,значениявнашемлежатслучае:промежутке0 ≤ y ≤между8, òî
|
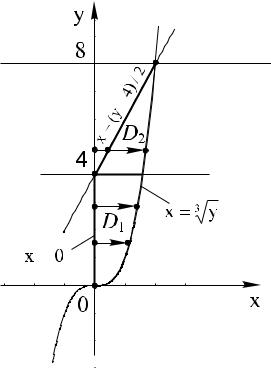
y = 0 è y = 8 (ðèñ. 14). |
|
|
|
|
Область |
èñ. 14 |
|
|
одной кри |
|
справа |
|
|
|||
войму |
3 |
|
|
|
|
|
|
|
|
- |
|
онаy =неx ,являетсяинтегрированияслевапростойдвумя:границаx ее= нужно0ограниченаy =разбить2x + 4,прямойпоэто |
|||||
yâèä= 4ункциональной(именноприy зависимости)= 4 |
наобластидве |
справа меняет |
|||
|
|
24 |
|
D1 |
D2. |
Таким образом, исходный интеграл сведется к двум по-
вторным интегралам по двум простым областямзначения |
|
|
|||||||||||||
Для области |
|
|
|
|
|
|
|
|
D1 |
D2. |
|
|
|||
является |
ункцией переменнойая |
y [0, 4] |
, |
переменная |
x |
||||||||||
D1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
y |
приним ет |
|
îò |
||||
x = 0 äî x = √y (об атн я ункция для y = x3 |
|
|
|
|
|||||||||||
(обратная |
|
y = x |
|
|
|
направлении, |
) в направ- |
|
|||||||
лении,Дляуказаннобластиîì ñò |
ëêàìè íà ðèñ. 14. |
|
|
|
|||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
является |
ункцией |
|
àÿ |
y [4 8] |
, |
переменная |
x |
||||||||
D2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
y |
принимàет значения от |
||||||
x = y |
|
4)/ 2ункция(обратнаядля ункция для y = 2x + 4) äî x = √ |
|
|
|||||||||||
− |
y |
||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Окончательнострелками на рисполучаем:.14. |
|
|
) â |
|
|
|
указанном |
|
|||||||
ZDZ |
|
|
|
ZDZ |
ZDZ |
|
|||
f(x, y)dxdy = |
f(x, y)dxdy + |
f(x, y)dxdy = |
|||||||
|
|
|
|
1 |
|
|
|
2 |
|
4 |
√y |
8 |
√y |
|
|
||||
|
3 |
|
|
|
3 |
|
|
|
|
привестисделодномуЗ = Z0 |
f(x, y)dx + Z4 dy |
|
|
|
|||||
dy Z0 |
Z |
f(x, y)dx. |
|
||||||
|
|
|
|
работечтоин вгралу,приåннрвегоîмгочтовычисленслучаенамивпоследствииувеличиваетпримераинтеграли, томожносвелсяможетвремя |
|||||
àтьмечание:выводкповторномуменьшейиз рассмотр, |
|
|
|
|
|
||||
втором к двум, что само по себе |
|
êîëè- |
|||||||
чество вычислений. Однако окончательный выв |
òîì, ê |
||||||||
ê êîìó (y−4)/2 î
виду приводить двойной интеграл, можн сделать в
налениезависимостипорядкадвойногоинтегрированияотвидаинтегралаункции.существенноf(x, y). В рядеупрощаетзадачперемевычис-
25
ЗадачаЗадачи1 для самостоятельного решения
Вычислить повторные интегралы:
1) |
3 |
|
5 |
|
2 |
|
x |
√ |
|
|
|
|
|
|
|
|
|
3 |
|
x |
|
|
|||||
3) |
|
dy |
(x + 2y)dx; |
2) |
|
dx |
|
|
|
|
|
dy; |
|
|
|
|
|
|
|
2 |
2 |
||||||
|
−3 |
y2−4 |
|
|
|
|
|
|
|
x +y |
|
|
|
|
|
0 |
|
x |
|
|
|||||||
|
2 |
ln y |
|
2π |
|
2 |
|
|
|||||
|
R |
|
R |
|
R |
|
R |
|
|
||||
5) |
|
dy |
exdx; |
4) |
|
cos2 xdx |
ydy; |
||||||
|
1 |
0 |
|
|
0 |
|
|
0 |
|
|
|||
|
R5 |
x |
|
3 |
|
2x |
|
|
|||||
|
R |
|
R |
|
|
|
|
|
R |
|
|
||
7) |
1 |
dxx3 (x − y)dy; |
6) |
2 |
dx x (x + 2y)dy; |
||||||||
|
2 |
1 |
|
|
2 |
|
x2 |
|
|
||||
|
R |
R |
(x2 + 2y)dx; |
|
R |
|
R |
|
|
||||
9) |
|
dy |
8) |
|
dx |
|
(2x − y)dy; |
||||||
|
0 |
0 |
|
|
1 |
|
x |
|
|
|
|
|
|
|
R1 |
R |
2 |
|
R |
π |
Rπ/2 |
|
|
||||
ЗадачаЗаписатьdy2 (двойнойy − x)dx;интеграл10) |
dx |
0 |
|
ex+sin y cos ydy. |
|||||||||
|
−3 |
y−1 |
|
0 |
|
|
|
|
|
||||
|
R |
|
R |
|
R |
|
R |
|
|
||||
|
|
Dâ |
|
RR |
|
пределы интегри- |
îáë ñòè |
|
|
|
f(x, y)dxdy по заданной |
||
àíèÿ |
|
|
D |
|
|
|
ðîâ1) |
|
|
томввидеиномповторного,порядке:расставив |
|
||
|
D треугольник, ограниченный прямыми: y = 0, |
|||||
y =2)3x, y = −x + 5; |
|
|
|
|||
|
D треугольник, ограниченный прямыми: x = 0, |
|||||
y =3)2x, y = x − 3; |
|
|
|
|||
|
D треугольник, ограниченный прямыми: y = 1 − x, |
|||||
y =4)2, y = 2x + 1; |
|
|
|
|||
|
D треугольник, ограниченный прямыми: x = 3, |
|||||
y =5)x, y = 3x; |
|
|
|
|||
|
D треугольник, ограниченный прямыми: y = −x + 1, |
|||||
y = 0, y = x + 3; |
26 |
|
|
|||

6) |
D область, ограниченнаякривыми: x = 1, y = x3 |
, |
|||||
7) |
√ |
|
; |
|
|
||
y = − |
x |
|
x = 1, y = −x3 |
|
|||
|
D |
|
|
||||
y =8)√ |
|
; |
|
|
|
||
x |
|
|
|
||||
|
|
D область, ограниченная |
кривыми: y = x + 1, |
||||
9) |
|
|
2; |
|
|
|
|
y = −x |
|
|
|
|
|
||
|
D область, ограниченная кривыми: y = 32 − x2 |
, |
|||||
y =10)−4x; |
|
|
|
||||
D область, ограниченная кривыми: y = 1/x, y = 6ex,
y =11), y = 6;
y = /x, y = 6;
x =13)12)9; D область, ограниченная кривыми: y = 3/x, y = 3√x, D область, ограниченная кривыми: y = √x, x = 16,
D область, ограниченная кривыми: x = 3, y = x−1, x =14)7, y = 1;
D область, ограниченная кривыми: x = 0, y = 0,
y =15)ln x, y = 2;
D область, ограниченная кривыми: x = 4, y = 2x, xЗадача=1)Вычислить1, y =3 0. двойные интегралы:
x2 +2)yRR= 2y (x > 0); |
||
|
xydxdy, где область D ограничена кривыми x + y = 2, |
|
D |
|
|
2 |
|
|
x = 4RR y = 1 x |
|
|
D (4 − y)dxdy, где область D ограничена кривыми |
||
2 3) y, |
, |
= 0 (x > 0); |
x = 0RR |
ex+ydxdy, где область D ограничена кривыми y = ex, |
|
D |
|
|
y = 2; |
27 |
|
y =5)x2RR, y = |
|
√x; |
|
|
|
||||||||||||||
|
4) |
|
|
(x + 2y)dxdy, где область D ограничена кривыми |
|||||||||||||||
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
x |
|
|
|
|
dxdy, где область D ограничена кривыми x = 0, |
|||||||
|
6) |
RR, |
2 |
|
|
|
2 |
||||||||||||
|
|
|
|
|
, |
|
|
|
√ |
|
|
; |
|||||||
|
|
|
|
|
x +y |
|
|
|
|
|
|
|
|
||||||
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x = 2 y = x |
|
|
|
y = |
3x |
|
|||||||||||||
|
7) |
|
|
(3 − x − y)dxdy, где область D êðóã x2 + y2 ≤ 1; |
|||||||||||||||
|
|
RR |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
A(0, |
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
RRB(1, 0) |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
xydxdy, где область D треугольник с вершинами |
||||||||||||||
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
8)0), |
|
|
|
|
|
|
|
|
|
|
, C(0, 1); |
|||||||
y =9)√RRx, y = 0; |
|
|
|
|
|
||||||||||||||
|
|
|
|
ydxdy, где область D ограничена кривыми x+y = 2, |
|||||||||||||||
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
+ |
RR |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
xydxdy, где область D ограничена кривыми x + y = 2, |
|||||||||||||||
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 10)y2 = 2y (x > 0); |
|
|||||||||||||||||
y =11)x2;RR |
|
y |
dxdy, где область D ограничена кривыми y = x3, |
||||||||||||||||
|
2 |
||||||||||||||||||
xy2dxdy, где область D часть круга x2 + y2 ≤ 9, |
|||||||||||||||||||
|
12); |
|
|
|
|||||||||||||||
|
|
|
D |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||
x = |
|
RR |
x2y2dxdy, где область D ограничена кривыми x = y2, |
||||||||||||||||
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x |
13)0; |
RR |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
≥ |
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
RR |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
D (2 − x − y)dxdy, где область D часть круга |
|||||||||||||||
2y 14)x2 + y2 |
|
≤ |
4; |
|
|
|
|||||||||||||
|
≤ |
|
|
|
|
|
√ |
|
|
|
|
ydxdy, где область D ограничена прямыми |
|||||||
|
|
|
|
|
|
|
x − |
||||||||||||
RR
D
4
y =15)x, y = x, y = 1, y = 4;
RR
вершинамиsin π(x − y)dxdy, где область D треугольник с
D
A(−4, 1), B(−1, −281/2), C(7/2, 17/2).
|
 |
3. |
Замена переминтеграленных двойном |
|
||
|
|
задач вычисление |
интегралов в |
åê ðòî |
||
вой систряде |
координат |
затруднитель |
||||
í |
ûì, ÷òî ìожет быть связано,вляется |
ой стороны, с достаточ- |
||||
ñë æí |
областью интегрировадвойныхостаточноия, другой стороны, |
|||||
ñ |
|
подынтегральной ункции. Для упрощения |
|
- |
||
ленийвидом этих случаях прибегают |
замене переменных. |
(8) |
||||
ãäå |
|
|
|
|
||
тегрируемаассмотримвзамкуíутойкциюобластиf(x, y), которая определенавычисин- |
||||||
в области |
|
D плоскости xOy. И пусть |
||||
|
|
|
Ω плоскости uOv задана система ункций |
|
||
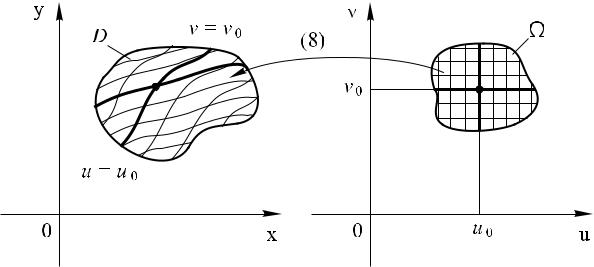
цииxпер(u, v) енныхи(8)y u, v) непрерывно ди еренцируемые ункластСèñòåìа задаетu и v.взаимнооднозначное отображение об-
Ω на область D (ðèñ. 15).
èñ. 15
29
Тогда
ZZ ZZ
ãäå f(x, y)dxdy = f (x(u, v), y(u, v)) |J|dudv, (9)
D Ω
|
D(x, y) |
∂x |
∂x |
|
|
|
|
|
||
|
|
|
∂u |
∂v |
|
|
|
|
|
|
ФункциональныйJ = J(u, v) = |
D(u, v) |
пределитель= |
|
= 0, |
|
(u, v) |
|
Ω. |
||
|
|
∂u |
∂v |
6 |
|
|
||||
|
|
|
∂y |
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ментателеометрическиплощадиЯкоби, илиприонякотображениивырби номжа . коэобластейJ ициентназывается.искаженияопределиэле--
èí |
егралемула.Координаты(9)элементормулаплощадизаменыявляютсяобластипеременныхдекартовыми. двойном |
|
|
|ÔîJ|dudv |
Ω |
|
областиu v |
коорди- |
òàìè точки (u, v) â |
интеграломкриволинейнымиΩ |
|
координатахва Еслив(9), вназываетсяисходном. |
- |
|
|
(x, y) интеграледвойнымDпо, областиинтеграл, стоящèнейныхспра |
|
ластьвменияу переменполуче ногоыхпов правойормуламчасти(8),(9)то областьюинтегралаD проинтегриростанетзвести обза- |
||
|
Ω, которая при правильном выборе ункций x(u, v), |
|
âычисленийсвоюассмотримчащеможеточередьинтеграловвсего.оказатьсячастныеиспользуютсяможет.привестислучаизначительноназаменыкпрактикеупрощениюпеременных,приисходной,дальнейшихвычислениикоточто- |
|
yдвойныхрые(u, v) |
|
Полярная система |
. |
полярныеВкачествекоординатыкриволинейныхкоторыекоординатu v рассмотрим r ϕ, 30 связаны с декартовы-
