
Tulenko Двойные интегралы
.pdf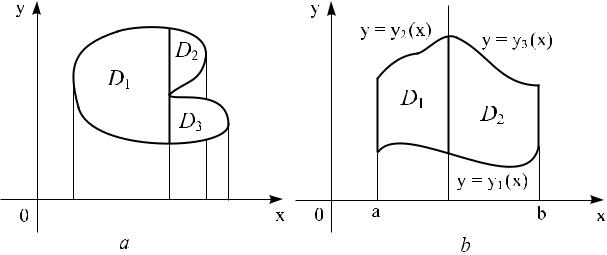
âèäее границыуравнения,(ðèñописывающего. 6, b) верхнюю или нижнюю часть
èñ. 6
Аналогично, чтобы роверить, что область интегрирова нияобластьем D являетсяизмененияпростойпеременнойотносительно оси Ox, за иксиру- оведем через каждую точку отрезкаy отрезок [c, d] îñè Oy, ïðямуюЕсли каждая(рис.7).такая прямая пересекает[c, d]границугоризонтальнуюоблсти
частиD не болееграницы,чем заключенныевдвухточкахмежду(условиепрямыми1),левая и прàвая опи ываются каждая одним явным уравнениемy = c è y = d,
|
|
x = x1(y) è |
|
простой относительносоответственнооси(услов |
2), то область |
D |
является |
x = x2(y) |
|
|
|
|
Ox и определяется условиями: |
нене,выполняетсяявляется простойодно. изотнусловий,повторномусительнобластьоси интегри- |
|
cрования≤Åñëèy ≤ d x1(y) ≤ x ≤ x2 |
(y) |
разбитьñведения1)разуЗамечание:еслипользоватьсянадвойногонепростыевыполняетсяинтеграланельзяпрямыми,.условиепараллельнымик1,тообластьосиормулойOxследуетдля(4)
8, a . |
11 |
Ox (ðèñ. |
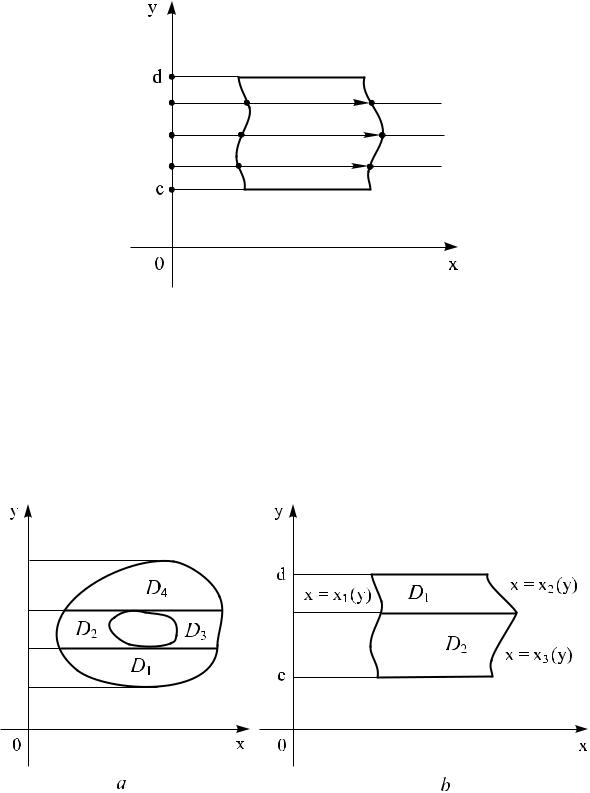
èñ. 7 |
то бласть нужно раз |
|
|
2) если не в полняется условие |
|
||
|
|
|
- |
û точкипрямыми,областипараллельными2, осиизменяетсяпро |
|||
бхотьящиминапростчерез |
|
Ox |
|
|
|
которыхправую часть ее |
|
видграницыуравнения,(рис.8,описывающегоb). |
левуюD èëè |
|
|
Если область |
èñ. 8сложная, то ее нужно пред- |
в рительно разбèòü |
конечное число простых областей, а |
затем значение двойнтегрированияого интеграла найти как сумму инте- |
|
|
12 |
гралов, вычисленных по каждой такой простой области в
кимдвух2)1)Итак,повторным;частнепосредственногосведениязадачай: двойноговычисленияoвычисления)интеграла. двойногокповторныходномуинтегралаилиинтеграловсостоитнескольиз-
отдельности (свойство 3
с помощью ормулы Ньютона Лейбница:
|
Za |
b |
ãäå |
f(x)dx = F (x)|ab = F (a) − F (b), |
ПримерВычислитьFассмотрим(x) 1первообразнаядвойнойнесколькоинтегралпримеровункции .f(x).
RR
f(x, y)dxdy от ункции
D
f(x, y) = x + y по области, ограниченной прямыми x = 0, этогоy =1.0Прежде,построимy = −xвсего+ 5прямые.изобразимешениеобласть интегрирования. Для
точки пересечения прямыхx ëè= 0обозначим,y = 0, y èõ:= −x + 5 найдем
араллельные оси |
x. Для этого проведем прямые, |
|
A(0, 0), B(5 0), |
Опред( исосей.длялим,9)координаты.всехявляетсяточек областиобластьнет. простой относительно |
|
Cодной(0Cначала2,.изменения5) |
|
òîê |
D определим промежу- |
будуткиполосыобласти,междусаманимиOyобласть.,Втак,нашемчтобыинтегрированпримереонипроходилитакимиялежалачерезпвнутриямымточ-
x = 0 è x = 5. Все точки13 области интегриðования
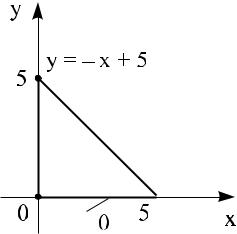
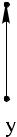
 èñ. 9
èñ. 9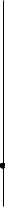
оказаваются.Изсунказаключеннымивидим,чтокаждаявнутри9)ресекаетоси полосыпрямая,0ïàð≤ x ллельная≤ 5 (ðèñ.
кахЗначит,ютсясительноOy(рискаждаяè.границуосипроходящая9),областьпричемоднимобластиинтегрированияуравнениемверхняячерезинтегрированиялюбуюнижняя.точкуявляетсяграницы,ровноотрезкапростойвдвухописыва[0, 5]отно,точпе-
реннем3.ляем исходяасставиминтегралахизOyпределыусловия.можемПределыинтегрированияиспользоватьвнутреннеговнешинтегралаîрмулувнешнем(3)расстав.ивнут-
ствует наменьшему значению0 ≤ x ≤переме5: ижнийной пред соответ- а верхний предел наибольшему значениюx, òî åñòü x = 0,
ыПределызависеть интеготпеðированияеменой |
интеграла xäîëæ= 5.- |
|
íåì èäåò ïî |
x, поскольку |
рование в |
щую нижнююy. границуНаниж обласийпредели, ставимэто ункц ю, задаю |
||
сти,предел ункцию, описывающую верхнююy = 0,границунаверхнийобла |
||
|
|
- |
|
расстановкевнутрьосиобластипределовинтегрированиявовнтрен |
|
внемположительноминтегралеy = −x +движемся5.направленииПри |
|
|
9). |
14 |
Oy по стрелке (см. рис. |

повторному:Око чательно получаем двойной интеграл, сведенный к
5 −x+5
ZZ Z Z
меннойтеграл4.Теперь.Сначалаост(xетсявычисля+ y)вычислитьdxdy = внутреннийdxполученный(x +интегралy)повторныйdy. переин-
D |
0 |
0 |
затем yвнешний,приэтоминтегралпереìеннуюпопеременнойx считаем постоянной, ла:полученной результате вычисления внутреннегоx от интеграункции-
|
5 |
|
|
−x+5 |
|
5 |
|
|
|
|
|
|
y2 |
|
− |
x+5 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Z dx |
|
Z |
(x + y)dy = Z dx xy + |
|
|
0 |
|
= |
|||||||||||||||||
|
|
2 |
|
|||||||||||||||||||||||
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
x(−x + 5) + |
|
|
+ 5)2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
dx = |
|
|
|
|
|||||||||||||
|
|
|
= Z0 |
(−x |
|
|
|
|
||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||
5 |
− |
|
|
|
|
|
x2 − 10x + 25 |
|
|
|
|
5 |
25 − x2 |
|
|
|||||||||||
= |
x2 |
+ 5x + |
|
|
dx = |
|
dx = |
|||||||||||||||||||
Z0 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Z0 |
|
|
2 |
|
|
|
|
|||
|
1 |
|
|
|
|
x3 |
5 |
|
1 |
|
|
|
125 |
|
|
|
|
|
|
2 |
|
|||||
|
|
|
|
|
+ 25x 0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Ответ= :2 |
− |
|
= |
|
|
− |
|
|
+ 125 = 41 |
|
. |
|||||||||||||||
3 |
2 |
3 |
3 |
|||||||||||||||||||||||
тельнокакЭтотобластьосиже41 |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
приминтегрированияможно былоявляетсярешитьпростойипо-другому,иотноситак- |
|||||||||||||||||||||||
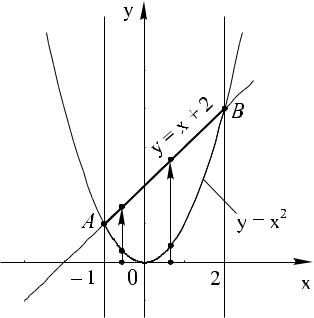
аналогичныеДлятогооси Oxчтобырассмо. этомреннымубедиться,выше, толькопроделаемотносительнодействия,
Ox. Точки области заключаем15 полосу, параллельную
осивающиеOx: 0область≤ y ≤ 5слева(рис.и10)справаи исследуем. |
кривые, ограничи- |
||
èñ. 10 |
|
|
(4), преде |
В этом случае можем применить |
|
|
|
лы интегрирования расст вляем аналогич |
рассмотренно- |
||
му выше, отличие заключàåòñÿ ëèøü |
том,ормулуч прежде, чем |
||
сставлять пределы инт грирования во внуòреннем интег- |
|||
гралевимицу,(онислева,дляункцию,этоданномнайтиункций,обратнуюобратныеслучаописывающихå будутункции,зависетьграницу.описывающейНаотнижнийпеременнойобластипределлевуюспра),- |
|||
ðàнужноваст |
|
|
y |
интегрирования,ную ункции,x =этоописывающей0, на верхнийправуюпределг аницуункцию,области-
ляем по стрелке вдоль положительнx = −y + 5, тогоестьнаправленияеделыраосистав- (рисВ.результате10). двойной интеграл сведется к повторному:Ox
5 |
−y+5 |
|
|
|
ZDZ (x + y)dxdy = Z0 dy |
Z0 |
(x + y)dx |
|
ïî ïåðå |
меннойТеперь сначала вычисляем внутренний и теграл |
|
|||
|
постоянной. |
|
|
|
числяемxвнешний,перемеиíнуютегралy считаемпопеременной |
Затем вы- |
|||
16 |
|
y: |
|
|

|
5 |
|
|
|
−y+5 |
|
|
5 |
|
x2 |
|
|
|
− |
y+5 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Z dy |
Z |
(x + y)dx = Z |
dy |
|
|
+ xy 0 |
|
= |
||||||||||||
|
2 |
|
|||||||||||||||||||
|
0 |
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
+ 5)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= Z0 |
(−y |
2 |
|
+ (−y + 5)y dy = |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
5 |
y |
2 |
− |
|
|
|
|
− y2 + 5y dy = 2 Z0 |
5 |
|
|
||||||||||
= Z0 |
2 |
|
|
|
(25 − y2)dy = |
||||||||||||||||
|
|
|
|
|
|
10y + 25 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
1 |
|
|
|
|
y3 |
5 |
|
1 |
|
|
|
125 |
|
|
2 |
|||
ПримерВычислВ = |
|
|
|
|
0 |
= |
125 − |
|
|
||||||||||||
2 |
|
25y − 3 |
2 |
3 = 41 |
3. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зультате2èть двойнполуîé÷аеминтегтотðалже ответ, что и пеðâûé ðàç.
f(x, y) = xy по области D, |
RR |
y = x |
|
|
|
|
f(x, y)dxdy от ункции |
||
|
|
D |
|
2, |
|
|
ограниченной кривыми |
|
|
|
|
|
|
|
y =1.xИзобразим+ 2. |
гра ическиешениебласть |
|
|
|
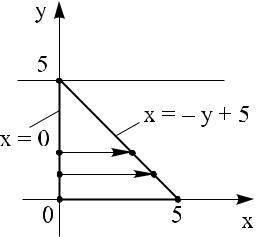
цийНайдем координаты точек пересеченияD (рисгра.11)иков. унк- y = x2, y = x + 2. Для этого решим систему уравнений
y |
= |
x2; |
y |
= |
x + 2. |
В результате получим две точки пересечения:
A(−1, 1) è
B(22,.4)Определим,. является ли17область простой.
|
|
èñ. 11 |
|
|
Cначала для всех точек области интегрирования |
||||
дилипромежутокпрямые,парализмененияельныекоординатыосиведем |
x. Для этогоопредепро |
|||
|
|
|
|
- |
|
области,междуасаманимиобласть,.так,Внашемчтобыинтегрированияслучаеонипрохэто |
|||
лежалачерезвнупрямые |
òриочкиполосы |
Oy |
|
|
заключеннымиx = −1внутриx = 2полосывсе точки области оказаваются |
||||
|
|
|
|
(рис.проходящая11). |
черезВидим,каждуючтоточкукаждаяотрезкавертикальная−1 ≤ x прямая,≤ 2 |
||||
ицу области |
[−1 2] îñè Ox пересекает гра |
|||
|
|
|
|
- |
нением,осирхняя тограницыестьобластьобластировноявляетсяописываютсядвухправильнойкаждаяпричемотноднимнижняясительноурав |
||||
â |
D |
точках, |
|
|
реннемормулуПределы3.Oyасставиминтегралах(3)можем.внешнегопределыдля.вычисленияинтегралаинтегрированияпоинтегралапеременнойвовнешнемиспльзоватьивнут- |
||||
ляем исходя из условия |
|
|
x ðàñ òàâ |
|
|
|
|
|
ñîîò- |
ветствует наменьшему возможному−1 ≤ x ≤ 2значению(нижнийперемнаибольшемупреднной |
||||
то есть значению |
|
|
x, |
|
|
x = −1, а верхний18 |
предел |
||

зависетьПределывозможномуотинтегрированияперемезначениюнойдлявнутреннеготочек области,тегрированието алаестьдолжныx = 2).
èäåò ïî |
|
|
|
|
|
|
|
|
|
|
|
|
x, поскольку |
|
|
|
|
|
|
|
|
|
|
|
|
|
â íåì |
|||||||||||||||
дающуюункцию |
|
|
|
|
|
|
|
|
|
|
|
|
области, |
на верхний предел2, çà |
||||||||||||||||||||||||||||
|
yнижнюю.Награницуий предел ставим ункцию y = x |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
расстановке, описыиксированнойающуюпределовверхнююточкивовнутреннемграницуобин |
|||||||||||||||||||||||||||||||||||
тегралести. То естьдляy =каждойприx + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
направленииобласти нтегрированияоси по стрелке |
полодви- |
||||||||||||||||||||||||||||||||||||||
æемсяительномвнутрь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x [−1, 2] |
||||||||||
Получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Oy (ðèñ. 11). |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
ZZ |
|
|
|
|
|
|
|
|
2 |
|
|
|
x+2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
4. Вычислим полученныйxydxdy =повторныйdx xydyинтеграл:. |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
−1 |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
x+2 |
|
|
2 |
|
|
|
|
|
|
|
|
y2 |
|
|
|
x+2 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
dx |
2 |
|
xydy = |
|
dx |
|
x |
|
x2 |
= |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
Z |
|
|
|
Z |
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
−1 |
|
|
x |
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
(x(x + 2)2 |
|
|
|
|
xx4) |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x5 |
|
|
|
|||||||||||
= Z |
|
− |
dx = Z |
x |
3 |
+ 4x |
2 |
+ 4x |
− |
dx = |
||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
x4 |
|
4x3 |
|
4x2 |
|
|
|
x6 |
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
+ |
|
|
|
|
+ |
|
|
|
|
|
− |
|
|
|
|
1 = |
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
4 |
|
3 |
|
2 |
|
|
6 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
32 |
|
|
|
|
|
|
32 |
|
|
1 |
|
|
|
4 |
|
|
|
|
|
|
|
1 |
|
2 |
|
|
5 |
|
|||||||||
Îòâåò: 16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= 2 |
|
|
|
+ |
|
|
|
+ 8 − |
|
|
− |
|
+ |
|
|
− 2 + |
|
|
1 = 5 |
|
. |
|||||||||||||||||||||
|
4 |
3 |
|
3 |
4 |
3 |
6 |
|
8 |
|||||||||||||||||||||||||||||||||
|
|
|
5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
сительноверим,ешимявляетсяосиэтот8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
желипримеробластьдругиминтегрированияспособом.Дляпростойэтогоотнпро- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
Ox. |
|
|
|
|
|
|
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
лямСначалавсехпрямые,точекзапараиксируемобполосыобласти,лельныеинтегрированияобласть изменения. Дляпеременнойэтого веy
ластьуравнениD описываеявляетсямивно |
точках, |
|
|
внутриочкигоризонтальнаямеждуñаманимиобласть, .так,Эточтобыпрямыеинтегрированияони ïðîõî- |
|||
лежалаäили через |
|
|
Ox |
|
|
|
y = 0 |
yê =æäóþ4. Каждаячкуотрезка |
|
прямая, проходящая через |
|
области |
|
[0 4] осиуравнением,Oy пе есекает границу об- |
|
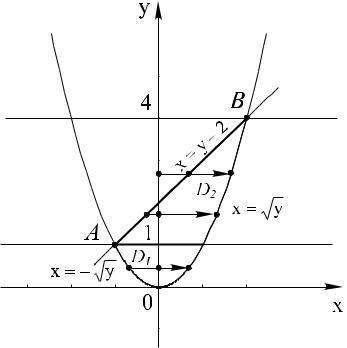
(состоитдвухпростойсяоднимиздвухотносительнооднакоучастков)ав.осиЗначит,леваячастьнашаграницыдвумяоб
зобьемПоэтомуобластьпрямой,прежде,интегрированияпараллельнойчемвоспользоватьсяосинадвепростыхсделать ормулойOx. .Это(4),можнора-
точку |
|
|
|
Ox и проходящей через |
границыA(−(рис1, 1). 12).которой соединяются два участка левой |
||||
|
|
èñ. 12 |
||
Получили две области |
|
è |
|
|
которыхИтак, |
ужесогласноможносвойствуприменять ормулу(рис.(4)12),. к каждой из |
|||
|
D1 |
|
D2 |
|
|
|
320(см. с. 5), имеем |
||
