
Tulenko Двойные интегралы
.pdfгде область |
|
D |
задана |
условиями: |
4x ≤ x |
2 |
+ y |
2 |
≤ 8x, |
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
14) |
√ |
|
|
; |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 x ≤ y ≤ |
|
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|||
где область |
|
|
|
|
ZDZ |
xydxdy, |
|
|
|
|
|
|
|||||
|
15) |
|
|
D задана условиями: (x − 1)2 + (y − 1)2 ≤ 1; |
|||||||||||||
|
|
|
|
ZZ |
|
|
|
|
|
|
|
|
|||||
где область |
|
|
|
|
x2 + y2dxdy, |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
D |
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
åгралапри решениик |
||||||
|
Двойные4. ПриложенияDинтегралызаданагеометрииусловиями:широкодвойногоиспользуютсяx +èçèêyèíò− 6x ≤ 0. |
|
|
||||||||||||||
|
азличных геометрических |
изических задач. ассмот |
|||||||||||||||
|
им некоторые основные примеры применения двойного ин- |
||||||||||||||||
теграла. |
|
|
|
|
Приложения к геометрии |
|
|
|
|
|
|||||||
|
1. Вычисление площади плоской области |
|
|
||||||||||||||
щадьПусть D ограниченная плоская область, тогда ее пло- |
|||||||||||||||||
|
â SD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
декартовойможно вычислитьсистеме координатпо ормулам: |
|
|
|
|
|
|||||||||||
|
в полярной системеSD = ZDZ dxdy, |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
координат |
|
|
|
|
|
(14) |
|||
SD = ZΩZ |
rdrdϕ, |
(15) |
41 |
|
|
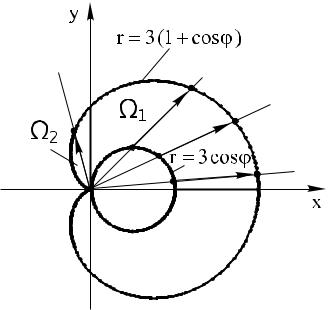
ìåíòЗамечание:площади преобразуетсяпри переходе кïîполярнымормуле координатам эле-
ПримернымиНайтивполярной7площадьdxdyсистеме:игуры,= |J|drdϕограниченной= rdrdϕ. кривыми, задан-
1. Изобразим игуру наешениеrплоскости= 3 cos ϕ, (ðèñr = 3(1. 20)+. cos ϕ). |
|
|
|
èñ. 20 |
- |
Из рисунка видим, что игура симметрична |
||
но полярной оси, поэтому для вычисления площади мож о |
||
вычислить двойной |
теграл только по верхнейотносительполови е |
|
|
|
- |
åчание:нияодной. ееизполученныйплощадиесличастей,гураможнорезультатрезуобладаетьтатвычислятьумножатьумножитьсимметрией,двойнойнанаколичдватоинте.для |
||
нахождгралствоигурыЗамчастейпоΩ/2 |
42 |
|
|
|
|

э ому2. Областьее нужноинтегрированияразбить на двеΩ/простые2 не являетсялучомпростой, позатемстиИспользуя.расставитьормулупределы(15),интегрированияполучаем по каждойϕ = π/îáëà2, à
S = 2 |
rdrdϕ = 2 |
π/2dϕ |
3(1+cos ϕ)rdr + |
π |
dϕ |
|
) |
= |
|
3(1+cos ϕrdr |
|||||||||
ZZ |
|
|
Z |
Z |
Z |
|
Z |
|
|
Ω/2 |
|
0 |
3 cos ϕ |
π/2 |
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
= 2 |
π/2dϕ |
|
|
|
Z |
|
0 |
|
|
|
|
2 3(1+cos ϕ)
r
2
+ |
π dϕ |
r2 |
|
3(1+cos ϕ) = |
|
|
|||
|
Z |
2 |
0 |
|
|
π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
= 9 π/2 |
(1 + cos ϕ)2 |
|
|
cos2 ϕ dϕ + π |
(1 + cos ϕ)2dϕ = |
||||||||||||||
|
Z |
|
|
− |
|
|
|
|
Z |
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 9 π/2(1 + cos ϕ)dϕ + |
π (1 + 2 cos ϕ + cos2 ϕ)dϕ = |
||||||||||||||||||
|
Z |
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 9 |
π/2(1 + cos ϕ)dϕ + |
|
π |
(1 + 2 cos ϕ)dϕ + π |
cos2 ϕdϕ = |
||||||||||||||
|
Z |
|
|
|
Z |
|
|
|
|
|
|
|
Z |
|
|
|
|
||
|
0 |
|
|
|
π/2 |
|
|
|
|
|
|
|
π/2 |
|
|
|
|||
|
|
|
π (1 + cos ϕ)dϕ + π |
|
|
|
|
|
dϕ |
|
|
|
|||||||
|
= 9 |
|
1 + cos 2ϕ |
= |
|
||||||||||||||
|
2 |
|
|||||||||||||||||
|
|
|
Z |
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|
|
|
Ответ:= 9 |
|
|
|
|
|
|
2ϕ + |
4 |
|
|
π |
|
|
4 π. |
|||||
(ϕ + 2 sin ϕ)|0π + |
|
|
|
π/2! = |
|
||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
sin 2ϕ |
|
|
|
|
45 |
|
|||
|
45 |
π. |
|
|
|
|
43 |
|
|
|
|
|
|
|
|
|
|
||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
Задачи для самостоятельного решения |
||||
Задача 5 |
|
|
|
|
||
Вычислить площади игур, ограниченных кривыми: |
||||||
21) x2 + y2 ≤ 9, x ≥ 0; |
|
|
|
|||
3 |
|
x2 + y2 ≥ 2x, x > y; |
|
|
|
|
4 |
|
x2 + y2 ≤ 2x; |
|
|
|
|
5 |
|
3y ≤ x2 + y2 ≤ 9, x ≥ 0, y ≥ 0; |
||||
6 |
|
1 ≤ x2 + y2 ≤ 2x; |
|
|
|
|
7 |
|
2x ≤ x2 + y2 ≤ 4x, y ≥ 0; |
|
|
|
|
8 |
|
x2 + y2 ≤ 4, y − x ≥ 0 |
|
|
|
|
90)x2 + y2 ≤ 3, x − y ≤ 0; |
|
|
|
|||
|
|
x2 + y2 ≤ 1; |
|
|
|
|
|
1 |
x2 + y2 ≤ 4, y ≥ 0, x ≥ 0; |
|
|
|
|
|
2 |
9 ≤ x2 + y2 ≤ 25; |
|
|
|
|
|
3 |
3x ≤ x2 + y2 ≤ 6x, y ≥ 0; |
√ |
|
|
|
|
4 |
4x ≤ x2 + y2 ≤ 8x, 21 x ≤ y ≤ |
3 |
x; |
||
15) (x − 1)2 + (y − 1)2 ≤ 1; |
|
|
|
|||
|
|
2 |
2 |
|
|
|
на Пусть2явным. Вычислениеx +непрерывноуравнениемy − 6x ≤площади0äè. еренцируемаяповерхностиповерхность зада
екцияповерхн верхности на zплоскость= f(x, y), ãäå (x, y) D, D ïðî- î вычисляется по ормулеxOy, тогда площадь этой
ZZ
q
площадиАналогичныеповерхности,ормулыеслиможноона заданазаписатьявнымдля нахожденияуравнением(16)
S = 1 + (zx′ )2 + (zy′ )2dxdy.
D
44
плоскостьx = f(y, z), ãäå (y, z) D, D проекция поверхности на
yOz: |
|
|
|
|
|
|
или уравнениемS = ZZ |
|
|
|
|
|
|
|
1 + (xy′ |
)2 |
+ (xz′ )2dydz |
(17) |
||
D |
q |
|
|
|
|
|
поверхности на плоскостьy = f(x, z), ãäå (x, z) D, D проекция
|
|
xOz: |
|
|
|
|
S = ZZ |
|
|
|
|
|
|
|
1 + (yx) |
|
+ (yz) dxdz. |
|
||
D |
p |
2 |
′ 2 |
|
|
|
|
|
′ |
|
(18) |
||
ПримерНайти8площадь части поверхности конуса |
||||||
íâûрезаемоймиоси из нее ци |
индром |
|
образующими 2параллель2 2-, |
|||
|
|
|
|
|
x + y |
= z |
Oz, направляющей которого служит кардиоида rовых=1.a(1ассматриваемаячастей,+ cos ϕ)симметричных.поверхностьшениеотно ительносостоитплоскостииздвуходина-
êаждаяплоскостиизкоторых |
св ю очередь симметрична относи, |
тельно |
xOy |
пуравнением:верхности,2.ВерхняябудетравумчастьíоженнойxOzплощадиповерх,поэтомуíаостиполовинычетыреконусаискомая. верхнейописываетсяплощадьчастиповерхявнымэтой
|
z =′ |
p |
x |
|
|
x |
|
′ |
|
y |
|
|
|
|
|
|
2 |
+ y2, поэтому имеем |
|||||
|
zx = |
|
|
, zy = |
|
|
|||||
|
p |
|
p |
|
|||||||
è |
x2 + y2 |
x2 + y2 |
|||||||||
q1 + (zx)2 |
+ zy 2 |
= s |
|
|
|
|
|
|
|
1 +45x2 + y2 |
+ +x2 + y2 = √2. |
||||||||
|
′ |
′ |
|
|
x2 |
|
y2 |
|
|
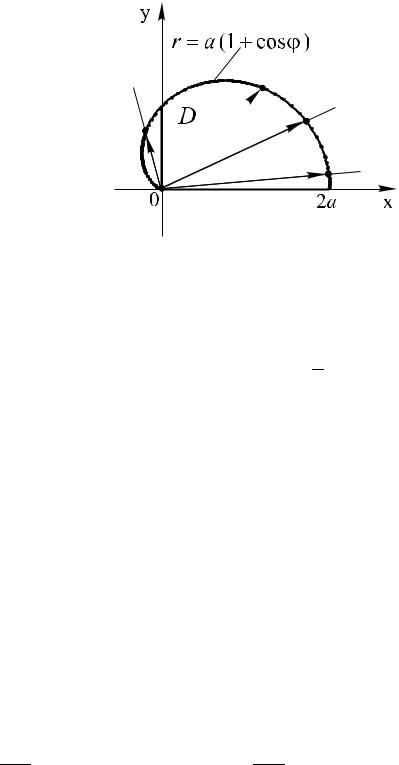
3. Половина верхней части поверхности
проектируется на плоскость xOyрассматриваемойобласть D (ðèñ. 21).
|
|
èñ. 21 |
|
|
Вычислим ее площадь, успользуя ормулу (16) и перей- |
||||
дя к полярной систеìе координат: |
|
|
||
|
|
|
|
- |
|
координатах,гран цасистемыобластивокоординат-интегрированиявторых,обусловлен,видомсамойужевозаданаобла-пер |
|||
ых,полярныхВыбортем,полярнойчто |
dxdy = √2 ZΩZ |
|
|
|
âñòè |
S1/4 = √2 ZDZ |
r dr dϕ. |
|
|
Ω которая является прост й |
|
определяется условиями: |
||||||||||||||||
0 ≤Сводяϕ ≤ πдвойной,0 ≤ rинтеграл≤ a(1 + cosк повторному,ϕ). |
получим |
|
||||||||||||||||
|
|
|
|
|
π |
|
a(1+cos ϕ) |
|
|
|
|
π |
|
|
|
|
||
S1/4 = √2 Z |
dϕ |
Z |
r dr = 2 |
|
Z dϕ (r2) |
|
0 |
= |
||||||||||
|
|
|
|
|
0 |
|
0 |
|
|
|
√2 |
0 |
|
|
a(1+cos ϕ) |
|
||
√ |
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
a2 |
ϕ|0π + 2 Z |
|
cos ϕ dϕ + |
|||||||
= 2 |
|
Z (1 + cos ϕ)2dϕ =462 |
|
|
||||||||||||||
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
π |
|
|
||
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
0 |
0 |

|
π |
|
dϕ = |
√ |
|
|
|
|
|
|
|
|
||
+ |
Z |
2 |
|
|
|
π + 2 sin ϕ |
|
0π + |
2 |
+ 4 sin 2ϕ |
|
0π |
= |
|
2 a2 |
| |
| |
||||||||||||
|
|
1 + cos ϕ |
|
2 |
|
|
|
|
π |
1 |
|
|
|
|
0
3πa2√2
4. Итак, искомая площадь= поверхности. равна
4
Ответ: S = 4 · S1/4 = 3πa2√2.
√
ЗадачаВычислитьЗадачи63πa2 площадьдля2. самостоятельногочасти по ерхности:решения
2 конуса2 2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+y |
2 |
= z |
2; |
||||||
1) x +y +z |
|
|
= 2, заключенной внутри конуса x |
|
|
|
|||||||||||||||||||||||
стями |
|
|
|
|
x2 |
+ y |
2 |
|
|
z2 |
|
, заключенн й между плоско- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
− x |
|
= 0; |
|
|
|
|
|
|
|
|
|
|||||||
3) |
цилиндра |
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x − 2y = 0 |
|||||||||||||||||
|
|
z = 0 |
|
|
|
x = 2z |
2 |
|
|
|
|
||||||||||||||||||
|
|
|
z = |
|
|
2 |
|
+ 1 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
√ |
|
|
|
2 |
|
|
|
|
|
, отсеченной плоскостями |
|
|
|
|
|
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4) |
|
x = 2 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
y = 2x |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
||
ïîверхностьложеннойy = x +âíàzпервом,плоскостьвырезаннойоктантецилиндром.Указание:xспроектировать+ z = 1 ðàñ- |
|||||||||||||||||||||||||||||
5) |
конуса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xOz; |
|
|
|
|
|
|
|
|
|
||||
|
цилиндра, |
|
|
x2 + z2 = y2, вырезаемой плоскостями x = 0 |
|||||||||||||||||||||||||
6) |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x + y = 2 y = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
z = x2, вырезанной плоскостями x + y = √ |
|
, |
||||||||||||||||||
|
,ñ åðû; |
|
|
|
2 |
||||||||||||||||||||||||
7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x = 0 y = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
зующими параллельнымиx + y + z = 1оси,вырезаемой цилиндром с обра- |
|||||||||||||||||||||||||||||
служит кривая |
|
|
|
|
|
|
|
|
|
|
|
Oz, направляющей которого |
|||||||||||||||||
8) |
конуса |
|
|
|
r = sin 3ϕ (òðåõ |
епестк вая роза); |
|
|
|
|
|
|
|||||||||||||||||
x + y |
|
= 2x |
2 |
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
x2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
z = |
|
|
|
+ y2, çàêëюченной внутри цилиндра |
|||||||||||||||||||
2 9) |
ñ2 åðû ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
стями |
|
|
|
x + y |
+ z |
|
= 1условии,расположенной между плоско- |
||||||||||||||||||||||
|
|
|
1 |
y è z = y ïðè |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
z = |
|
|
47 |
÷òî z ≥ 0, y ≥ 0; |
|
|
|
|
|
||||||||||||||||||
|
|
√ |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
3 |
|
|
|
|
|
||||||||||||||||||||||
âûøå0) |
плоскостиz = x, заключенной внутри цилиндра x2 + y2 = 4 |
||
11) |
ñ åðû |
z = 0; |
|
|
|
x2 +y2 +z2 = 1, заключенной внутри цилиндра |
|
2 |
2 |
|
|
xõó +13непрерыв..yВычислениеассмотрим= y. ой поверхностьюцилиндрическоеобъема цилиндрическоготело, ограниченноетеласвер |
|||
и вырезающими из плоскости xOy |
D (ðèñ. 22). Oz |
||
|
|
z = f(x, y), ãäå f x, y ≥ 0, |
|
ñêîé(x, y)поверхностьюD, изу плоскостьюобразущими,xOy областьпараллельнымисбокуцилиндричеоси-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
èñ. 22 |
|
|
|
|
|
|
||
|
|
|
|
|
|
Объем такого тела может быть вычислен по ормуле |
|||||
2. ас мотрим V = ZDZ |
f(x, y)dxdy. |
|
|||
пространственное тело |
(19) |
||||
ñтямиверху и ñнизу непрерывно |
|
|
поверхноое |
||
|
|
|
ди еренцируемымиV , ограничен |
||
z = f(x, y) è z = g(x, y48), ãäå (x, y) D соответствен-

но, сбоку цилиндрической поверхностью с образующими,
параллельными оси Oz (ðèñ. 23).
Объем такого тела равен èñ. 23 
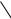
ZZ
ЗадачаЗадачи7V äëÿ= самостоятельного(f(x, y) − g(x, y)) dxdyрешения (20)
Вычислить объемыD тел, ограниченных поверхностями:
1)2 x2 + y2 = 8, x = 0, y = 0, z = 0, x + y + z = 4; 3 z = 4 − x2, 2x + y = 4, x = 0, y = 0;
4 z = 5x, x2 + y2 = 9, z = 0;
5 z = x + y + 1, y2 = x, x = 1, y = 0, z = 0; 6) x2 + y2 = 2z, x2 + y2 − z2 = 4, z = 0;
z = 3 − x2 − y2, z = 0; 49
87) z + x2 + y2 = 1, x = 0, y = 0, y = 4, z = 0;
90)z = x2 + y2, y = x2, y = 1, z = 0; z = y2, x2 + y2 = 4 z = 0;
11 z = 4x2 + 2y2 + 1, z = 1, x + y = 3, x = 0, y = 0;
1.ассмотримВычислениеy = x2, z плоское=Приложения0, массыz = òåëî,2 −плоскогоy.кот роеизикезанимаеттела область
плоскости D ностную плотностьxOy и имеет непрерывн распределенную поверх-
Массу этого телаρ(x, y), ãäå (x, y) D.
mD можно вычислить по ормуле |
|
интеграла2Замечание:.Вычисление. в mD = ZDZ |
ρ(x, y)dxdy. |
этомстатическихсостоит изическиймоментовсмысли координатдвойного |
|
центра тяжести п |
òåëà |
имеетПус ьнепрерывноплоскоетеëраспределеннуюоскогозанимает областьповерхностнуюплоскостиплот |
|||||||||||||
ностьжести |
|
|
|
|
|
|
|
|
|
|
D |
xOy |
|
|
|
ρэтого(x, y),телагде определяются(x, y) D, тогдаиз координатыормул: центра тя- |
|||||||||||
по ормулам: |
Ox è Oy соотвеòñòвенно, |
вычисляются |
|||||||||||
|
|
|
x |
|
= |
Mx |
, |
y = |
My |
|
|
||
|
|
|
|
c |
|
m |
|
c |
m |
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
ãäå |
m |
масса тела, а |
Mx |
, |
My |
ста ические |
моменты тела |
||||||
|
|
|
|
|
|||||||||
относительно осей |
|
|
|
|
|
|
|
|
|
||||
|
Mx = ZDZ |
y · ρ(x, y)dxdy, 50 My = ZDZ |
x · ρ(x, y)dxdy. |
||||||||||
