
Tulenko Двойные интегралы
.pdf
ми координатами x è y ормулами
x = r cos ϕ,
ди Здесьеренцируемыми,ункции, стоящиеаyякобиан= справа,r sin ϕ. являются непрерывно
|
|
|
∂x |
∂x |
|
|
sin ϕ |
|
|
|
|
|
D(r,ϕ) |
|
|
∂r |
∂]phi |
|
|
r cos ϕ |
|
||||
D(x,y) |
|
|
∂r |
∂ϕ |
|
= |
|
cos ϕ |
− |
r sin ϕ |
= r |
|
è Jормула(r, ϕ) =çàìåíû= |
|
∂y |
∂y |
|
|
|
|
|
||||
|
переменных имеет вид |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ZZ ZZ
симметрию,дят,Замечание:еслиf(x,исходнаяy)dxdyподынтегральнаяк=об астьярнымf (xинтегрирования(rкоординатамcos ункцияϕ), y(r sinзависитϕимеетобычно)) rdrdϕоткруговуюперехо. (10)-
D |
Ω |
|
полярная координаты)система координат |
+ y2 |
. |
|||
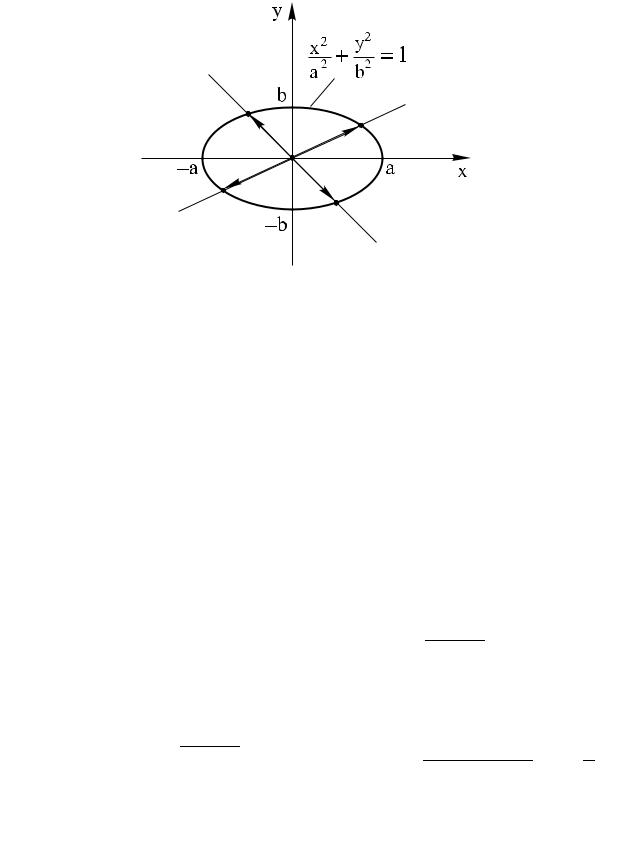
ЗдесьОбобщенная(эллиптические |
x2 |
|
||||
ãäå |
y |
= |
br sin ϕ. |
(11) |
||
|
x |
= |
ar cos ϕ, |
|
|
|
Âa,ýòîìb положительныеслучаеякобиан числаравен. |
|
|
||||
|
|
D(x, y) |
|
|
||
и ормула заменыJпеременных(r, ϕ) = |
принимает= abr âèä |
|
|
|||
|
|
D(r, ϕ) |
|
|
||
ZZ |
f(x, y)dxdy = ab ZZ |
f (31x(ar cos ϕ), y(br sin ϕ)) rdrdϕ(12). |
||||
D |
Ω |
двойноголярныхПри вычислениикоордининтегрàòàõ,ëàдекартовыхдвойныхиспользуютповторныминтегралов,ихжепоследующегоправилазаписанныхсведениявыïî-
числения, что в координатах.

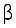

 èñ. 16
èñ. 16
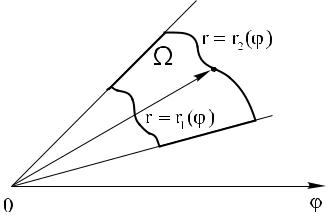
естьЕслиопределяетсяобластьΩ неравенствами:имеетвид,изображенный на рис. 16, то
онакповторномуназываетсяпопростойормуле:и двойной интеграл можно све- |
|
стито |
ϕ1 ≤ ϕ ≤ ϕ2, r1(ϕ) ≤ r ≤ r2(ϕ), |
ϕ2 r2(ϕ)
ZZ Z Z
интегралах1)Дляfëèáî(r cosсстанпроизϕ,используютr sinвкиодятϕ)пределовrdrdϕаналитическоедва=подхода:интегрированияdϕ преобразованиеf(r cos ϕ, rповторныхsin ϕîáëà)rdr(13).-
Ω |
ϕ1 |
r1(ϕ) |
координсти D в декартовыхтах, затемкоординатахизображаютправилам,область Ω |
олярных |
||
|
Ω на плоскости |
||
приасставляют(этовычислениивозможно,пределыинтеградекартовыми);поскопоëьку декартовойплоскостирассмотреннымсистемекоор |
|||
uOvординатвыше |
|
|
|
динаты |
|
uOv |
- |
u è v являются |
32 |
|
|

2) либо преобразование областей не производят, сов-
системоймещают .декартовуПределы интегрированиясистемуплоскостипо xOyрасставляютполярной
|
полюсе) |
координат точки |
|
производятэтом,исследуя закон изменения |
|
r ϕ |
|
отождествляя ее |
òî÷ê é |
|
(r, ϕ), |
(этопреобразуютотносительнлучи,центромобычнограисходящиеперическивнаходекоординатныхпраизêтикеполюса,полярн.областикоординатамприийлинийвычисленииконцентрическиесистеме.Исследоваполяркоордидвойой |
|||
ванияокружностисистемеыхЗамечание:интегралов |
(x, y |
|
D |
т изображают |
исходную |
бласть интегриро |
|
гральнуюобластьD, ункцию, уравненияполярнымкривых, ограничивающихподынте-
ПримеринтегралПереходяазберемD4, несколькообластькполярнымΩ,примеровкаккоординатам,правило.невычислитьизображаютдвойной.
y 10 |
RR p |
|
|
ãäå D полукруг x2 + y2 ≤ 4, |
|
x2 + y2dxdy |
|||||
|
D |
||||
≤ |
.Изобразим область интегрированияешение |
||||
|
|
|
|
||
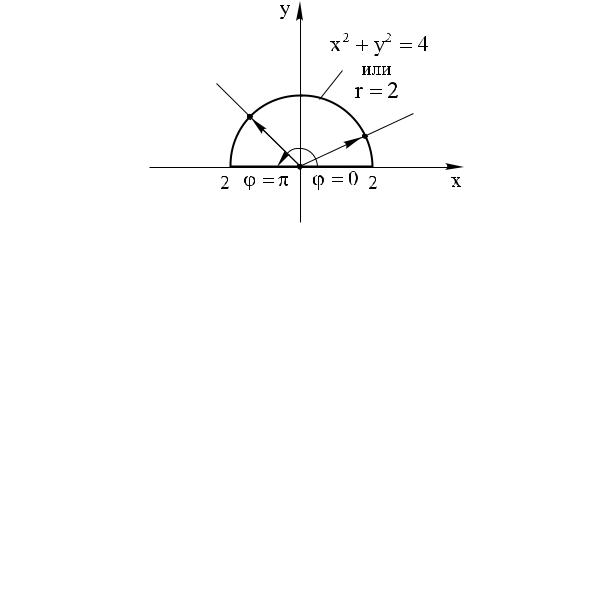
круг2. Перейдемсцентром кв полярнымначалекоординаткоординатам(рис. подынтегральную17)D,. строимормулам:полу- |
|||||
x ункцию:= r cos ϕ, y |
= r sin ϕ |
преобразуем |
|||
p
Запишемf(r cosдвойнойϕ, r sin ϕинтеграл) = (r cosв полярнойϕ)2 + (r sinсистеме:ϕ)2 = r.
ZZ ZZ
f(r cos ϕ, r sin ϕ33)rdrdϕ = r2drdϕ.
Ω Ω
|
|
|
èñ. 17 |
|
|
|
|
3. Cведем получеíный интеграл к повторному и вычис- |
|||||||
ëèì åãî. |
|
|
|
|
|
|
é èëè åå |
С ачала определим, является ли область пр |
|||||||
жно будет |
|
|
|
. Äëÿ ýòîã |
ст вместим |
||
полярную систему координатпростыедекар овой, проведем äâà |
|||||||
луч , исходящих |
начала коорди ат, |
чтобы все точки |
|||||
|
|
|
|
|
ними,облатак,ñтиамиинтегрировалучисодер |
||
областижалинияВ(риснашемхотяD. 17)лежалбыприм.разбиватьоднуревнутриграничнуюэтолучимеждуточку |
|
|
|||||
зом,условиюдля |
|
точек |
|
|
|
|
îáðà- |
|
âñåõ |
|
области |
олярныйϕ = 0 è ϕóãîë= πудовлетворяет.Таким |
|||
àждый17)х,координатпричем.такойсначалаилуч.пересекающиеТеперьпересекаетвначалепроведемграницуобластькоординатлучи,интегрированияобластиисходящиепридвухз |
|||||||
началаК.(ристочк |
0 ≤ ϕ ≤ π |
|
|
|
|
||
x = 0,
определяютсяке,y =принадлежащей0 что соответствуетуравнениемполуокружности,значениюr координаты= 0, затемкоторойточ
стеме соответствует кривойx2 + y2 =интегрирования4, что полярной ситворяютТакимусловиям:образо , точки областиr = 2 (рис. 17). удовле-
жемЗначит,воспользоватьсяобластьинтег0 ≤ îϕð≤ированиямулойπ34, (13)0 ≤является.r ≤ 2. простой, и мо-

Имеем
|
|
|
|
|
|
|
|
π |
|
2 |
|
|
|
π |
3 |
2 |
8 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Îòâ ò: |
r2drdϕ = |
dϕ |
r2dr == |
|
dϕ r3 |
0 |
= 3π. |
|||||||||||||
|
ZZ |
|
|
|
|
|
Z |
|
Z |
|
|
Z |
|
|
|
|
|
|
||
|
|
Ω |
|
|
|
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|||
ПримеринтегПе |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
вычислить двойной |
|||||||||
|
ðеходяал5 к полярным координатам, |
|
|
|
|
|
|
|||||||||||||
|
|
|
3 |
π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
dxdy |
|
|
|
|
|
D определена условиями |
||||||||
|
|
|
D |
|
(x2+y2)2 , где область |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Изобразим область интегрешениерован я |
|
|
|
|
|||||||||||||||
|
|
RR |
≤ 8x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4x ≤ x + y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
окружности:чала построим кривые, ограничèвающие нашуD. Дляобластьэтого. снаЭто- |
||||||||||||||||||||
|
|
|
|
|
2 |
2 |
|
|
2 |
2 |
заметнопереходе.декартовойОбластьтегрирования,заключенанеполярнымсистемеявляеттак- |
|||||||||
коордибудетсямеждуЗамечание:простойвесьма |
|
|
|
|
|
|||||||||||||||
|
|
íнимиатам (рисxупроститсязатруднительнымвычисление+данная.y18)=.4xобластькакинтегралаx +область.yинтегрированияПри= 8x |
||||||||||||||||||
поды тегральная ункция, что |
|
|
|
облегчит вычис- |
||||||||||||||||
ления. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Перейдем к полярным координатам по ормулам: |
||||||||||||||||||||
и запишем подынтегральнуюx = r cos ϕ, yункцию= r sin âϕ âèäå |
|
|
|
|||||||||||||||||
ластьЗапишемf(x, yóðàâ) = f(åíèÿr cos ϕ,окружностей,r sin ϕ) = |
|
|
1 |
|
|
1 |
|
|||||||||||||
|
ограничив= àþ.ùèõ îá- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(x2 |
+ y2)2 |
r4 |
|||||
ПолучаемD, в полярнойдля первойсистемеокружности:35координат.


 èñ. 18
èñ. 18 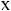





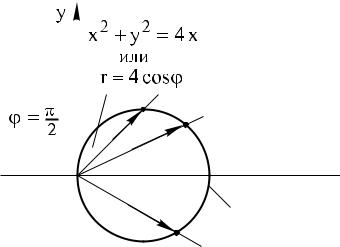
xè2äëÿ+ y2второй:= 4x, |
r2 cos2 ϕ + r2 sin2 ϕ = 4r cos ϕ, r = 4 cos ϕ |
|||||||||
2 |
|
2 |
|
|
2 |
2 |
|
2 |
2 |
|
полярнойИспользуяx +y =системе8x, ормулуrкоординат:cos ϕ(10),+r запишемsin ϕ = 8rдвойнойcos ϕ, интегралr = 8 cos ϕâ. |
||||||||||
силилимдекартовой3.нетегоCведем.. |
ZDZ |
f(x, y) dxdy = ZΩZ |
1 |
|||||||
r4 rdrdϕ. |
||||||||||
|
|
|
|
чтобыпропределсовместимведем двам,нтегралсодержполярнуюявлуча,етсякповторномуàлиходящихлисистемуобластькоординатизпростойначалавычис- |
||||||
|
|
ДляСначаланими,этогополученный |
|
|
|
|||||
π |
ϕ |
|
|
|
ϕ = |
|
π |
ϕ = |
π . Òàêèм образом, для |
|
|
π . Теперь провåäåì ëó÷è, исходящие из начала |
|||||||||
|
|
|
|
|
|
|
|
|
|
- |
примерекоординат,чнуюмеждуточкуэтотак,учиобластисамивсеинтегрированиялучиточкиобëа ти(рхотяDс. лежали18)бы. однуВнашемвнутгра |
||||||||||
всех точек области |
|
− |
2 |
|
2 |
|||||
|
|
|
|
|
|
полярный угол удовлетворяет условию |
||||
− 2 ≤ |
|
≤ |
2такойпересекающиелучпересекает36областьграницуинтегрированияобластив (рисдвух. |
|||||||
18)координатКаждый. |
|
|
|
|
|
|
|
|
||

точках,затем причемокружностьсначала пересекает окружность r = 4 cos ϕ,
определяетсями на рис. 18).условиями:Областьr =интегрирования8 cos ϕ (навлениеявляетсяуказанопростойстрелкаи-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
π |
4 cos ϕ ≤ r ≤ 8 cos ϕ. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 2 ≤ ϕ ≤ 2 |
|||||||||||||||
4. Используя ормулу (13), получаем, |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π/2 |
|
|
8 cos ϕ |
|
|
|
|
|
|
|
ZΩZ |
|
1 |
rdrdϕ = ZΩZ |
1 |
drdϕ = Z |
dϕ4 cosZ ϕ |
1 |
dr = |
|
|||||||||||||||||||
|
|
r4 |
r3 |
r3 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−π/2 |
|
|
|
|
|
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|
8 cos ϕ |
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|
|
|
|
|||
= dϕ |
|
−2r2 |
|
|
2 |
|
|
|
|
−64 cos2 ϕ + 16 cos2 ϕ |
|
|
dϕ = |
||||||||||||||||
|
|
4 cos ϕ = |
|
|
Z |
|
|
||||||||||||||||||||||
|
Z |
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
||||||||||||
|
π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|
|
|
|
|||
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
= 128 |
|
|
Z |
|
cos2 ϕ dϕ = 128 |
|
|
|
|
= −64. |
|
|||||||||||||||||
|
|
|
|
−cos ϕ π/2 |
|
||||||||||||||||||||||||
|
|
|
3 |
|
|
|
π/2 |
|
|
1 |
|
|
|
|
|
3 |
|
1 |
|
|
− |
3 |
|
|
|
||||
Îòâ |
ò: |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
интегПримерПеðеходяал6− 3ê. полярным координатам, вычислить двойной
64
D |
q |
|
|
|
ãäå D |
a2 |
+ b2 |
≤ 1 |
1 − a2 |
+ b2 dxdy |
|||||||
RR |
|
x2 |
y2 |
|
x2 |
y2 |
||
1 Область интегрированияешение |
|
|
. |
|||||
поренность2. ормуламВданномэллипсапримерес ц нтромпереходначалеD кпрполярнымдставляеткоординаткоособой(ðдинатамис.внут19). -
гральнаяобраз ым, такункцияxêàê= ïðèr cosметтакойϕ, достаточноy =заменеr sin ϕпеременныхсложныйнеявляетсявид:подынтецелесо-
r |
− |
a2 |
|
b2 |
f(r cos ϕ, r sin ϕ) = 1 |
(r cos ϕ)2 |
+ |
(r sin ϕ)2 |
|
|
|
|||
37 |
|
|
|
|
è |
|
|
|
|
|
|
èñ. 19 |
|
|
|
|
|
|
|
|
|
||
|
усложнит вычисления. |
|
|
|
|
|
|
|
|
|
||||||||
|
сильноПоэт му воспользуемся обобщенныìè ïîлярными коор |
|||||||||||||||||
д натами (11). При такой замене подынтегральная унк |
||||||||||||||||||
öординаèÿ3.имеетЗапишемах:âèä |
границу области |
интегрирования. в новых ко |
||||||||||||||||
|
√ |
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
f(a r cos ϕ, b r sin ϕ) = |
|
1 − r |
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
вить, что областьr = 1являетсяилиr =простой1. Èç |
|
|
|
|
|
условиями:устан |
||||||||||||
рисунказадаетсялегко |
|
|
|
|||||||||||||||
0ê ≤повторному:Вычислимϕ ≤ 2π, двойной0 ≤ r ≤ 1интеграл,. используя (12) |
сведя его |
|||||||||||||||||
|
|
|
|
|
|
|
2π |
|
1 r√1 − r2 dr = |
|
|
|||||||
|
ZDZ |
f(x, y)dxdy = ab · Z0 |
dϕ Z0 |
|
|
|||||||||||||
|
2π |
|
|
1 |
√1 − r |
|
|
|
|
|
|
(1 r2)3/2 1 |
|
2 |
||||
|
ab |
|
|
|
|
|
|
|
|
|
||||||||
|
òâåò: |
dϕ Z0 |
|
2 |
2 |
) = − 2πab |
|
− |
|
|
0 |
|
3πab. |
|||||
= −Î 2 Z |
|
|
d(1−r |
|
3 |
|
= |
|||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 πab. |
|
|
38 |
|
|
|
|
|
|
|
|
|
|
|||
|
Задачи для самостоятельного решения |
||||||||||
Задача 4 |
|
|
|
|
|
|
|
|
|
|
|
Вычислить двойные интегралы, перейдя к полярным ко- |
|||||||||||
ординатам: |
|
|
|
|
|
|
|
|
|
|
|
1) |
|
|
|
|
|
|
|
|
|
|
|
где область |
|
ZDZ |
xy2dxdy, |
||||||||
2) |
|
D задана условиями: x2 + y2 ≤ 9, x ≥ 0; |
|||||||||
где область |
|
|
ZDZ |
|
ydxdy, |
||||||
3) |
|
D задана условиями: x2 + y2 ≥ 2x, x > y; |
|||||||||
|
|
|
ZDZ |
|
|
|
|
y2 |
|||
где область |
|
|
|
|
|
dxdy, |
|||||
|
|
|
x2 + y2 |
||||||||
4) |
|
D задана условиями: x2 + y2 ≤ 2x; |
|||||||||
|
ZZ |
|
|
|
|
|
|||||
где область |
|
|
9 − x2 − y2dxdy, |
||||||||
|
|
D |
p |
|
|
|
|
|
|||
y ≥5)0; |
|
D задана условиями: 3y ≤ x2 + y2 ≤ 9, x ≥ 0, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ZZ |
|
y |
2 |
|
|
|||
где область |
|
|
|
dxdy, |
|||||||
|
|
x |
|||||||||
|
|
|
D |
|
|
|
|
|
|||
6) |
|
D задана условиями: 1 ≤ x2 + y2 ≤ 2x; |
|||||||||
|
|
|
|
ZZ |
|
xdxdy,39 |
|||||
D

где7)область |
D задана условиями: 2x ≤ x2 + y2 ≤ 4x, y ≥ 0; |
||||||
где область |
|
ZDZ (x + y)dxdy, |
|||||
8) |
D задана условиями: x2 + y2 ≤ 4, y − x ≥ 0; |
||||||
где область |
|
ZDZ (x − y)dxdy, |
|||||
9) |
D задана условиями: x2 + y2 ≤ 3, x − y ≤ 0; |
||||||
|
ZZ |
|
|
|
|
|
|
где область |
cos(π |
|
x2 + y2)dxdy, |
||||
|
D |
|
|
p |
|||
10) |
D задана условиями: x2 + y2 ≤ 1; |
||||||
где область |
ZDZ |
e−(x2+y2)dxdy, |
|||||
11) |
D задана условиями: x2 + y2 ≤ 4, y ≥ 0, x ≥ 0; |
||||||
|
ZZ |
p |
|
|
|
|
|
где область |
x2 + y2 − 9dxdy, |
||||||
|
D |
|
|
|
|
|
|
12) |
D задана условиями: 9 ≤ x2 + y2 ≤ 25; |
||||||
где область |
ZDZ (x2 + y2)dxdy, |
||||||
13) |
D задана условиями: 3x ≤ x2 + y2 ≤ 6x, y ≥ 0; |
||||||
|
|
ZDZ |
|
dxdy |
|||
|
|
(x2 + y2)2 , |
|||||
|
|
|
|
40 |
|
|
|
