
Tulenko Двойные интегралы
.pdfВспом3. Вычислениеим,некоторчто моментовй осиинерцравенèпроизведениюнерцииматериальнойплоскоготочкиòåëàэтойот- |
|
чки на квадрат |
асстояния от нее до этой оси,массы |
инерциисительностемы |
точек равен сумме момент |
тов инерции всех точ к.
Тогда моменты ин рции плоского тела относительно ко
ординатныхмулам: осей OxматериальныхOy могут быть вычислены по ор-
|
2 |
|
2 |
момент инерции относительно начала координат равен(21) |
|||
àIx = ZDZ |
y · ρ(x, y)dxdy, |
Iy = ZDZ |
x · ρ(x, y)dxdy, |
I0 |
= ZDZ (x |
2 |
+ y |
) · ρ(x, y)dxdy èêà,= Ix + Iy. |
|
|
|
2 |
|
огранич нного(22) |
|
прямымиПримерНайти 9моменты инерции треуголь |
|||||
x + yоординат,= 2 x = 2, y = 2, относительно осей Ox, вOyкаждой1.Изобразимначалаточêе пропорциональнатреугольникеслиешеегонаиеплоскостиповерхностнаяординатеэтой(областьточкиплотность.
рисВершинами.24). треугольника являются точки D íà
A(2, 0), B(2, 2),
Cтельноника(02Ïî,.2)вВычислимусловию.каждойкординатныхточкезадачимоментызадаетсяосейповерхностнаяинерциивыражениемо муламтреугольникаплотность(21). треугольотноси--
51 |
ρ(x, y) = ky, ãäå |
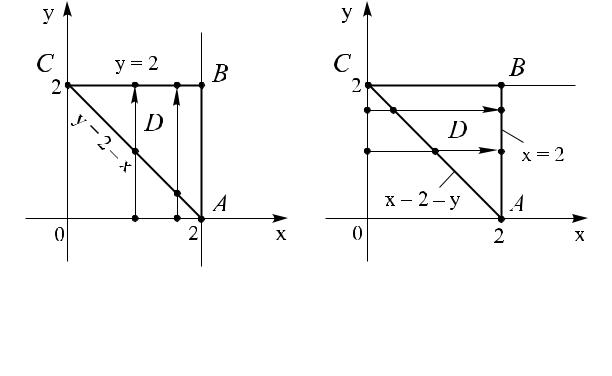
èñ. 24 |
kрованиякоэ ициент пропорциональности, а область интегри- |
24)Имеем.D является простой относительно обеих осей (рис. |
Ix = ZZ |
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
||||||
|
y2 · kydxdy = k Z |
dy Z |
|
y3 dx = |
|
|
|||||||||||||||||||
|
|
D |
|
|
|
|
|
|
|
|
0 |
|
|
2−y |
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
y5 |
2 |
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= k Z |
y3(2 − 2 − y)dy = k Z |
y4 dy = k |
|
|
0 = |
|
|
k, |
|||||||||||||||||
5 |
5 |
||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Iy = ZZ |
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|||||
x2 · kydxdy = k Z |
|
dx Z |
x2y dy = |
||||||||||||||||||||||
|
|
D |
|
|
|
|
|
|
|
|
0 |
|
|
2−x |
|
|
|
|
|
|
|
|
|||
2 |
|
|
y2 |
2 |
|
|
k |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= k Z x2 dx |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x = |
|
Z x2 4 − (2 − x)2 |
|
|
dx = |
||||||||||||||||||
2 |
− |
2 |
|
||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
2 |
|
|
|
|
|
|
k |
|
|
− |
|
x5 |
|
2 |
24 |
|
|
|
|||||
= 2 |
Z (4x |
3 |
− x |
) dx =5 2 x |
4 |
5 |
|
0 = 5 k. |
|||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

для упрощения вычис ений при нахожде-
нииЗамечание:I I
порядокначалаСогласноx координатинтегрированияy (22),повторныхвычислимкаксуммуинтегралах. моментполученныхбылинерциивыбранрезультатов:относительноразличный
Ответ: |
|
I0 = Ix + Iy = |
56 |
k. |
|
|
|
||||
|
|
|
5 |
|
|
|
32 |
24 |
56 |
|
|
треугольникаЗадачи8 для самостоятельного решения |
|||||
Задача |
Ix = 5 k, |
Iy = 5 |
k, I0 = 5 k. |
||
1. Н йти массу |
|
имеющей орму прямоуголь- |
|||
плотностьгокатетадо в любойпластинки,точкекатетамиравнаABрасстоянию= a, BCîò=ýòîéb, еслиточкиее ры2( НайтиBCкоординаты. центра тяжести однородной игу-
ность3.ρНайти= c), ограниченноймоментыинерциикривымитреугольника,xy = 4 yимеющего2 = 16x, x ïëîò= 4. -
ρ = c ограниченного прямыми x + y = 1, x + 2y = 2, y =40Найти,относительномассу пластинки,осейOx ограниченнойOy. кривыми
√
y = x2,
yнородной=5. Определитьx, еслипластинкиееповерхностнаякоординаты(цеплотностьтратяжестиравнаплоскойρ = x + îä2y-.
ρ = c), огра иченной кр выми y = x2, ординатy =6.2xВычислить2, x =игуры,1 x =момеогра2. íтиченнойинерциипрямымиотносительно начала ко-
x + y = 2, x = 0,
yðû=7(.0,Найтиеслиρкоординаты= 1. центра тяжести однородной игу-
ρ(x, y) = c), ограниченной53 кривыми y = x, y2 = 3x.

8 Вычис ить моменты инерции треугольника однород |
|||||||||||
|
|
|
|
|
пластинки, |
|
|
|
|
||
ного. треугольника (статическиеρ = c) вершинами A(2 2), B(0, 2)-, |
|||||||||||
ниче9 Наной. тикривымимассуи |
|
ìîì íòû |
|
|
|
îãðà |
|||||
C(2, 0) |
|
|
|
|
|
|
|
|
|
|
|
ïëîòíîñòü |
y = 4 − x2, y = 0, если ее поверхностная |
||||||||||
ниченной10.Найтиэллипсомρ =моментыa. |
инерции однородной игуры, огра- |
||||||||||
|
|
x2 |
y2 |
|
|
|
|
|
|
, |
|
относительно1Найтимассуначалапластины,координатограниченной, относительно.кривымиосей |
|
|
Oy |
||||||||
|
|
a2 |
+ b2 |
= 1 |
|
|
Ox |
|
|||
|
|
|
|
|
|
|
y = x2, |
||||
2 |
Определитьеслиограниченнойееповерхностнаякоординатыкривымицентрапло ностьтяжести однородной. |
||||||||||
пластинки, |
|
|
|
|
|
|
|
|
|
|
|
y = √x |
|
|
√ |
ρ = x + 2y |
|
|
|
|
|||
âûìè |
|
|
|
|
2 |
|
|
êðè.- |
|||
3 Определить массу плоского тела, ограниченного, |
|||||||||||
|
|
|
|
y = 2x − x |
|
y = 0 |
|
||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
14. yНайти= 4xмоменты+ 4, y =инерции−2x + 4,однороднойеслиρ(x, y) =игуры2y. ( |
|
|
|
|
|||||||
граниченной кардиоидой |
|
|
|
ρ = c), |
|||||||
îñåé |
|
|
|
r = a(1 + cos ϕ), относительно |
|||||||
15.OxНайти,Oy имассуотносительнокруглой началапластиныкоординат(. |
≤ 1) |
|
|
|
|
||||||
верхностной плотностью |
x2 + y2 |
|
|
|
ïî- |
||||||
|
|
|
ρ(x, y) = 2 − x − y. |
|
|
|
|
|
|
||
54
Список литературы |
|
||
[1 |
Л. Д. Краткий курс математического ана- |
||
|
Кудрявцевлиза : 2 т./ Л.Д. Кудрявцев. М. : Физматлит, 2005. |
||
|
Ò. 2. 424 ñ. |
|
|
[2 Сборник задач по математическому анализу : в 3 т./ |
|||
|
Л. Д. Кудрявцев [и др. . М. : Физматлит, 2003. Т. 2. |
||
|
504 ñ. |
|
льными |
[3 Сборник задач по высшей математике: с |
|||
|
аботами. яды интегра ы. Векторныйконтри |
мплекс |
|
|
ный анализ. Ди еренциальные уравнения. Теория âå- |
||
|
роятностей. Опе ационное исчисление./ К. Н. Лунгу |
||
|
[и др. . М. : Айрис |
Пресс, 2007. 592 с. |
|
[4 Данко П. Е. |
математика в у ражнениях и за |
||
|
никова. М. Высшая: .Данко,шк. 1986. Ч. 2. 415 с. |
Кожев- |
|
|
дачах : в 2 ч./ П. Е. |
À. . Ïîïîâ, Ò. ß |
|
55
|
|
Содержание |
|
Введение . . . . . . . . |
|
||
1 |
Двойной интеграл . . . . . . . . . . . . . . . |
||
2 |
Вычисление войного интеграла декартовой |
||
3 |
системе |
координат |
к повто ному) |
Замена |
|
(сведениедвойном интеграле |
|
4. |
|
ния двойного интеграла к геометрии |
|
Приложизикпеременных. . . . . . . . . . . . . . . . . . . . .
Литература . .
3
6
29
41
55
56
Учебное издание
Туленко Елена Борисовна ДВОЙНОЙ ÈÍÒÅ ÀË, Е О СВОЙСТВАЕОМЕТСПОСОБЫИИ
ВЫЧИСЛЕНИЯ. П ИЛОЖЕНИЯ К ФИЗИКЕ
Учебно-методическое пособие для вузоведактор А. Ю. Котлярова
57
