
m08-15
.pdfФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
ЗАДАНИЯ ДЛЯ КУРСОВОЙ РАБОТЫ
ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ (ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ)
Учебно-методическое пособие для вузов
Издательско-полиграфический центр Воронежского государственного университета
2008
Утверждено научно-методическим советом факультета ПММ 11 февраля 2008 г., протокол № 5
Составители: Г.А. Виноградова, А.А. Ларин, Н.В. Рогова, П.С. Украинский
Рецензент д. ф.-м. н. И.Я. Новиков
Учебное пособие подготовлено на кафедре дифференциальных уравнений факультета прикладной математики, информатики и механики Воронежского государственного университета.
Рекомендовано для студентов второго курса факультета прикладной математики, информатики и механики Воронежского государственного университета.
Для специальностей: 010501 – Прикладная информатика и механика, 010901 – Механика, 010503 – Математическое обеспечение и админист-
рирование информационных систем
2

Введение
Курсовая работа предусмотрена программой курса математического анализа. Пособие содержит 25 вариантов заданий для курсовой работы по математическому анализу. Задания предполагают индивидуальную работу студентов для более глубокого освоения раздела «интегральное исчисление функций многих переменных». При решении задач можно использовать литературу, список которой приведен в конце пособия.
Вариант № 1
1. В двойном интеграле ∫∫ f (x, y)dxdy перейти к полярным координатам
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r и |
ϕ , полагая x = r cosϕ , y = r sin ϕ , и |
записать |
интеграл |
|
в |
виде |
||||||||||||
|
ϕ |
|
r |
(ϕ) |
|
|
|
|
|
|
|
|
− x}≤ x2 |
|
|
≤ 4}. |
|||
|
∫2 |
dϕ |
2 |
∫g(r,ϕ)dr , где D = {(x, y) : min{ x2 + y2 |
+ x, 3 x2 |
+ y2 |
+ y2 |
||||||||||||
|
ϕ1 |
|
r1 (ϕ) |
D = {(x, y) : x + y ≤ 3, |
|
|
|
|
y ≥ 0}. |
|
|||||||||
2. |
Вычислить ∫∫(x 2 + y 2 )dxdy , где |
x ≥ 0, |
|
||||||||||||||||
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Переходя к полярным координатам x = r cosϕ , |
y = r sin ϕ |
(или обоб- |
||||||||||||||||
|
щенным полярным координатам x = ar cosα ϕ , |
y = br sinα ϕ ), вычис- |
|||||||||||||||||
|
лить площадь области, ограниченной кривой |
x 4 |
|
+ |
y 4 |
|
= |
x 2 |
+ |
y 2 |
. |
|
|||||||
|
a 4 |
b4 |
h2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
k 2 |
|
||||||||
4. |
Найти объем x 2 + y 2 + z 2 ≤ 2cz , |
x 2 + y 2 ≥ 2az (a < c ≤ 2a) . |
|
|
|
|
|
||||||||||||
5. |
Найти площадь поверхности z 2 |
= 2xy , если 0 ≤ x ≤ a, |
0 ≤ y ≤ b . |
|
|||||||||||||||
6. Записать ∫∫∫ f (x, y, z)dxdydz интеграл в виде одного из повторных в сфе-
D
рической системе координат, если D = {(x, y, z) : x 2 + y 2 + z 2 ≤ 8z −8, 3(x 2 + y 2 ) ≤ z 2 }.
7. Записать ∫∫∫ f (x, y, z)dxdydz в виде повторного интеграла, выбрав одну
D
из систем координат (декартову, цилиндрическую или сфериче-
|
скую), если D = {(x, y, z) : 0 ≤ z ≤ 4 − x 2 , |
x 2 − y 2 ≥ 0, x ≥ 0}. |
|
||||||||||||||
8. |
Найти |
|
|
|
объем |
|
6 |
тела, |
ограниченного |
поверхностью |
|||||||
|
|
x 2 3 |
y |
2 3 z 2 3 |
|
z |
|
|
|
|
|||||||
|
|
|
|
|
+ |
|
|
+ |
|
|
|
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
a |
b |
c |
|
|
h |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||
9. |
Найти массу тела плотностью |
ρ = y , |
ограниченного поверхностями |
||||||||||||||
2x + z = 2a , x + z = a , y2 = ax, y = 0 ( y ≥ 0) .
10. Плотность в каждой точке прямоугольника пропорциональна квадрату расстояния от этой точки до одной из его вершин. Найти момент инерции этого прямоугольника относительно его сторон, проходящих через эту вершину, длины которых соответственно равны a и b .
3
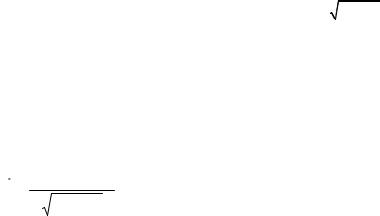
11. Найти массу части однородного параболоида z = |
1 |
(x2 |
+ y2 ), 0 ≤ z ≤1 |
|
2 |
||||
плотности ρ . |
|
|
||
|
|
|
12. Вычислить поверхностный интеграл ∫∫| x + y |dS , где S – часть по-
|
|
|
|
S |
|
|
|
|
|
|
|
|
верхности геликоида x = u cos v , |
y = u sin v , |
z = v , |
0 ≤ v ≤ 2π , |
0 ≤ u ≤1 . |
||||||
13. |
Найти координаты |
центра |
масс |
дуги |
винтовой |
линии |
|||||
|
L = {(x, y, z) : x = a cost, y = a sin t, z = bt , |
0 ≤ t ≤ π}. |
|
|
|
|
|
|
|||
14. |
Вычислить криволинейный интеграл первого рода |
∫ |
|
ds |
, где L – |
||||||
|
x − y |
||||||||||
|
отрезок АВ, А = (0,–2), В = (4,0). |
|
|
|
|
L |
|
|
|
||
|
|
|
|
|
|
∫(2 − y)dx + xdy , |
|||||
15. |
Вычислить криволинейный интеграл второго рода |
|
|||||||||
|
взятый вдоль ориентированной кривой |
|
|
|
|
L |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
L ={(x, y) : x = t −sin t, |
y =1 −cos t, |
0≤ t ≤ 2π}, |
где |
кривая |
прохо- |
|||||
|
дится по возрастанию параметра. |
|
|
|
|
|
|
|
|
|
|
16. Пользуясь формулой Стокса, вычислить ∫(xy +z)dx +(yz +x)dy + y |
a2 −x2 dz, |
|||
где L – кривая |
|
L |
|
|
x2 +y2 + z 2 = 2ax , |
x2 +y2 = a2 , положительно ориенти- |
|||
рованная на внутренней стороне цилиндра. |
|
|
||
17. Вычислить |
поверхностный |
интеграл |
второго |
рода |
∫∫(x2 + y2 )dydz + ( y2 + z 2 )dzdx + (z 2 + x2 )dxdy , где S |
– внутренняя сторона |
|||
S |
|
|
|
|
поверхности тела x2 + y2 + z 2 ≤ a2 , |
x ≥ 0, y ≥ 0, z ≥ 0 . |
|
||
JG |
, если F = |
−ix + jy + kz , где i, j, k |
– единичные орты. |
18. Найти div F |
|||
|
|
x2 + y2 |
|
19.Пусть u – скалярное поле. Доказать, что div (u u) = u u + ( u)2 .
20.Под действием силы g , направленной по оси OZ , тело единичной
массы скатывается от точки A = (a,0,2πb) до точки B = (a,0,0) |
по спи- |
||||||
рали x = a cosϕ, y = a sin ϕ, z = b(2π −ϕ) . Найти работу поля. |
|
||||||
21. Найти поток векторного поля |
F = (x3 + yz)i + ( y3 + xz) j + (z3 + xy)k в |
||||||
направлении внешней нормали через поверхность S : x2 + y2 |
+ z 2 =16 , |
||||||
z ≥ 0 . |
|
|
|
|
|
|
|
|
|
|
Вариант № 2 |
|
|
||
1. В двойном интеграле |
∫∫ f (x, y)dxdy |
перейти к полярным коор- |
|||||
динатам r и ϕ , полагая |
D |
|
|
|
|||
x = r cos ϕ , |
y = r sin ϕ , и записать интеграл в |
||||||
ϕ |
|
r |
(ϕ) |
D = {(x, y) : x2 |
+ y2 ≤ max (2ax, 2ay)}. |
|
|
виде ∫2 |
dϕ |
2 |
∫g(r,ϕ)dr , где |
|
|||
ϕ1 |
|
r1 (ϕ) |
|
|
|
|
|
4
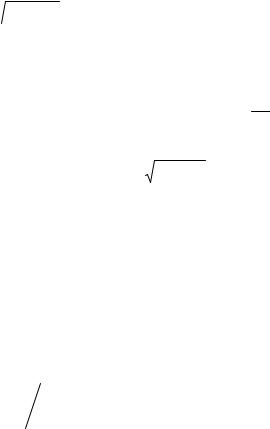
2. Вычислить ∫∫ | x − y 2 |dxdy , где D ={(x, y) : | y |≤1, 0 ≤ x ≤ 2}.
| x − y 2 |dxdy , где D ={(x, y) : | y |≤1, 0 ≤ x ≤ 2}.
D
3. Переходя к полярным координатам x = r cos ϕ , щенным полярным координатам x = ar cosα ϕ ,
лить площадь области, ограниченной кривой x 4 a 4
4. Найти объем тела x 2 + y 2 + z 2 ≤ a 2 , x 2 + y 2 ≥ a(a −
y = r sin ϕ (или обоб- y = br sinα ϕ ), вычис-
+ |
y 4 |
= |
x 2 y |
. |
b4 |
|
|||
|
|
c3 |
||
2z) . |
|
|
|
|
5. |
Найти площадь поверхности z = x2 + y 2 |
, если x 2 + y 2 ≤ 2ax . |
|
6. |
Записать |
∫∫∫ f (x, y, z)dxdydz интеграл в виде одного из повторных в |
|
|
|
D |
D = {(x, y, z) : x 2 + y 2 + z 2 ≤ 2 yR, |
|
сферической системе координат, если |
||
|
x 2 + y 2 ≥ z 2 }. |
|
|
7. |
Записать |
∫∫∫ f (x, y, z)dxdydz в виде повторного интеграла, выбрав одну |
|
|
|
D |
|
из систем координат (декартову, цилиндрическую или сферическую), если D ={(x, y, z) : 0 ≤ z ≤ 4 − x, y 2 ≤ 2x +2}.
8. |
Найти |
|
|
|
объем |
|
|
тела, |
|
ограниченного |
поверхностью |
||||||||||
|
x2 |
|
y2 |
z |
2 4 |
|
4 |
4 |
x2 |
|
y2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
= z |
|
k |
|
|
|
|
|
|
|
|
|
|
2 |
+ |
|
2 + |
|
|
|
|
2 |
+ |
|
2 |
|
|||||||
|
|
b |
c |
2 |
|
|
b |
. |
|
||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|||||
9. |
Найти массу тела плотностью ρ = z2 , ограниченного поверхностями |
||||||||||||||||||||
2x2 +2y2 −4ax−4ay +az =a2 , 2x2 +2 y2 −4ax −4ay +az =0 , z=0 M (a, a, a) V . 10. Найти момент инерции относительно начала координат однородной
пластинки плотности ρ , |
занимающей область, ограниченную ли- |
ниями x2 + y2 = 9 , x + y = 0 , |
x − y = 0 ( x ≥ 0 ). |
11.Найти массу части цилиндра x2 + z 2 = 2az , лежащей внутри конуса
x2 + y2 = z2 , если плотность ρ = | y | .
12. Вычислить поверхностный интеграл ∫∫| xy |dS , где S – поверхность
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
тела, |
образованного |
пересечением |
цилиндров |
x2 + z2 |
= a2 , |
||||||||
13. |
y2 + z 2 |
= a2 . |
|
|
|
|
|
L = {(x, y, z) : x = a(t −sin t), |
||||||
Найти |
координаты центра |
масс дуги |
||||||||||||
|
y = a(1 − cos t), |
z = 4a sin |
t |
, |
0 ≤ t ≤ 2π}. |
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
||||||
14. |
Вычислить |
криволинейный |
интеграл |
первого |
рода |
|
|
∫yds , |
||||||
|
L = {(x, y) : y = sin x, 0 ≤ x ≤ π}. |
|
|
|
|
|
|
|
L |
|||||
|
|
|
|
|
|
|
|
|
||||||
15. |
Вычислить криволинейный интеграл второго рода ∫ |
ydx + xdy |
, |
где |
||||||||||
1 + x |
2 |
y |
2 |
|||||||||||
|
|
|
|
|
|
|
|
L |
|
|
|
|
||
L – отрезок АВ, А = (0,0) и B = (1,1).
5

16. |
Пользуясь формулой |
Стокса, вычислить ∫xyzdx + y2 zdy + zx2 dz , |
где |
||||||
|
|
|
|
|
|
L |
|
|
|
|
L – кривая x2 +z 2 = a2 , |
z2 +y2 = a2 , |
x ≥ 0 , положительно ориентирован- |
||||||
|
ная на внешней стороне первого цилиндра. |
|
|
|
|||||
17. Вычислить |
поверхностный |
|
интеграл |
второго |
рода |
||||
|
∫∫xz2 dydz + yx2 dzdx + zy2 dxdy , где S |
– внешняя сторона поверхности тела |
|||||||
|
S |
|
|
|
|
|
|
|
|
|
x2 + y2 + z 2 ≤ 2az , x ≥ y , x2 + y2 ≥ 3z 2 . |
|
|
|
|
||||
18. |
JJG |
|
|
|
|
|
|
|
|
Найти div F , если F = r , где r = (x, y, z) . |
|
|
|
||||||
19. |
Пусть u, v – скалярные поля. Доказать, что div(u v) = u v + u v . |
|
|||||||
20. |
Найти работу поля F , где F – упругая, направленная к началу ко- |
||||||||
|
ординат и пропорциональная удалению точки от начала координат, |
||||||||
|
вдоль кратчайшей дуги |
эллипса |
x = a cos t, |
y = bsin t |
от точки |
||||
|
A = (a,0) до точки B = (0,b) . |
|
|
|
|
|
|
||
21. |
Найти поток векторного поля |
F = (xy + x2 )i + (2y − 2xy) j + (z − yz)k в |
|||||||
|
направлении внешней |
нормали |
через поверхность S : |
x2 + y2 |
= z 2 , |
||||
|
0 ≤ z ≤ H . |
|
|
|
|
|
|
|
|
|
|
|
Вариант № 3 |
|
|
|
|||
1. |
В двойном интеграле |
∫∫ f (x, y)dxdy |
перейти к полярным координатам |
||||||
|
|
|
D |
|
|
|
|
|
|
|
r и ϕ , полагая |
x = r cos ϕ , |
y = r sin ϕ , и записать интеграл в виде |
||||||
ϕ2 |
r2 (ϕ) |
|
|
|
2 |
2 |
||
∫dϕ ∫g(r,ϕ)dr , где |
|
|
|
a |
y |
|||
D = |
(x, y) : x 2 |
+ y 2 |
≤ |
|||||
x |
2 |
|||||||
ϕ1 |
r1 (ϕ) |
|
|
|
|
|
||
2. Вычислить ∫∫sgn(x 2 |
+ y 2 |
−4)dxdy , где |
D = {(x, |
|||||
|
D |
|
|
|
|
|
|
|
≤ 3a 2 , x ≥ 0, y ≥ 0 .
y) : x2 + y 2 ≤ 9}.
3. Переходя к полярным координатам x = r cos ϕ , |
y = r sin ϕ |
(или обоб- |
||||||||||
щенным полярным координатам x = ar cosα ϕ , |
y = br sinα ϕ ), |
|
вычис- |
|||||||||
|
x |
4 |
|
y |
4 |
|
2 |
|
y |
2 |
3 |
|
лить площадь области, ограниченной кривой |
|
+ |
|
|
x |
|
+ |
|
|
|||
|
4 |
|
4 |
|
2 |
|
2 |
|||||
|
|
= |
|
. |
||||||||
|
h |
|
|
k |
|
a |
|
|
b |
|
|
|
4. |
Найти объем тела a 2 ≤ y 2 + x 2 ≤ b2 , x 2 − y 2 |
− z 2 ≥ 0 , x ≥ 0 . |
|
5. |
Найти площадь поверхности 2z = x 2 , если |
x ≤ 2y ≤ 4x , x ≤ 2 |
2 . |
6. |
Записать ∫∫∫ f (x, y, z)dxdydz интеграл в виде одного из повторных в |
||
|
D |
D = {(x, y, z) : x 2 + y 2 |
|
|
сферической системе координат, если |
+ z 2 ≤ 2yR, |
|
x 2 + y 2 ≤ z 2 }.
7. Записать ∫∫∫ f (x, y, z)dxdydz в виде повторного интеграла, выбрав одну
D |
|
|
|
из систем координат (декартову, |
цилиндрическую |
или |
сфериче- |
скую), если D = {(x, y, z) : x + y + z ≤ 2, |
0 ≤ 4z ≤ 4 − x 2 − y 2 , |
y ≥ 0, |
x ≥ 0}. |
6

8. Найти |
|
|
|
|
|
объем |
|
тела, |
|
|
|
|
ограниченного |
поверхностью |
||||||||||||
|
|
2 |
|
|
2 |
|
|
2 |
|
4 |
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
x |
|
y |
|
z |
|
|
|
|
x |
|
y |
|
z |
|
|
|||||||||||
|
|
+ |
|
+ |
|
|
|
|
|
π z |
|
|
|
+ |
|
+ |
|
|
|
|
||||||
|
a |
2 |
b |
2 |
c |
2 |
|
|
= sin |
c |
|
a |
2 |
b |
2 |
c |
2 |
. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9.Найти массу куба со стороной a , если плотность его в каждой точке равна квадрату расстояния этой точки до фиксированной вершины куба.
10.Найти координаты центра тяжести однородной пластинки, имеющей форму кругового сектора с углом α и радиусом R .
11. |
Найти массу части конуса |
x2 = y2 + z 2 , лежащей внутри цилиндра |
|||||||||
|
x2 + y2 = 2ax , если плотность ρ = x . |
|
|
|
|
|
|
||||
12. |
Вычислить поверхностный интеграл ∫∫(x − y)dS , |
где S |
– |
часть ци- |
|||||||
|
|
|
|
|
|
S |
|
|
|
|
|
13. |
линдра x2 + y2 = a2 , x ≥ 0 , лежащая внутри цилиндра |
z 2 = a(a − x) . |
|||||||||
Найти координаты силы притяжения однородной полуокружности |
|||||||||||
|
массой M и радиусом R массы m , помещенной в центре |
соответст- |
|||||||||
|
вующей окружности. |
|
|
|
|
|
|
|
|||
14. |
Вычислить криволинейный интеграл первого рода |
∫(x2 |
+ y2 )ds , где |
||||||||
|
L – отрезок АВ, А = (0,1), В = (–2,3). |
|
|
|
L |
|
|
||||
15. |
|
|
|
|
|
|
|||||
Вычислить криволинейный интеграл второго рода |
∫(−x2 ydx + xy2 dy) , |
||||||||||
|
где L ={(x, y) : |
|
|
|
|
|
|
|
L |
|
|
|
x2 + y2 = r 2 } – окружность, которая обходится в поло- |
||||||||||
|
жительном направлении. |
|
|
|
|
|
|
|
|||
16. |
Пользуясь формулой Стокса |
вычислить |
∫z 2 xdx + ( y + z + x)dy + y2 zdz , |
||||||||
|
где L – кривая |
|
|
|
|
|
L |
|
|
|
|
|
x2 +y2 = ax , |
x2 = y2 |
+ z 2 , |
положительно ориентиро- |
|||||||
|
ванная на внешней стороне цилиндра. |
|
|
|
|
|
|||||
17. Вычислить |
поверхностный |
интеграл |
второго |
рода |
|||||||
|
∫∫yz2 dydz + zy2 dzdx + yx2 dxdy , где S – внешняя сторона поверхности тела |
||||||||||
|
S |
|
|
|
|
|
|
|
|
|
|
|
x2 + y2 ≤1, x ≥ 0, y ≥ 0 , 0≤ z ≤ x2 + y2. |
|
|
|
|
|
|
||||
18. |
JG |
|
r |
|
|
|
|
|
|
|
|
Найти div F , если F = |
, где r |
= (x, y, z) , r =| r | . |
|
|
|
|
|||||
|
|
|
|
|
|||||||
|
|
|
r |
|
|
|
|
|
|
|
|
19.Пусть u,v – скалярныеполя. Доказать, что grad (u + v) = grad u + grad v .
20.Найти работу поля F , где F – сила, имеющая постоянную величину
и направленную вдоль оси OY вдоль кратчайшей дуги эллипса x = a cos t, y = bsin t от точки A = (a,0) до точки B = (0,b) .
21. Найти поток векторного поля F = (x − y + z)i + ( y − z + x) j + (z − x + y)k в направлении внешней нормали через поверхность S : | x | + | y | + | z |=1.
7

Вариант № 4
1. В двойном интеграле ∫∫ f (x, y)dxdy перейти к полярным координатам
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r и |
ϕ , полагая x = r cos ϕ , |
y = r sin ϕ , и записать интеграл в виде |
||||||||||||||||||||||||||||||||
|
ϕ |
|
r |
(ϕ) |
|
|
|
|
|
|
|
|
|
|
|
|
+ y 2 )}. |
|
|
|
|
|
|
|
|
|
|||||||||
|
∫2 |
dϕ |
2 |
∫g(r,ϕ)dr , где D = {(x, y) : a 2 |
≤ x 2 + y 2 |
≤ a( y + |
|
x 2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
ϕ1 |
|
r1 (ϕ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Вычислить ∫∫([x] +[ y])dxdy , |
где |
D – квадрат с вершинами |
|
O (0,0), |
||||||||||||||||||||||||||||||
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
A (0,2), В(2,0), С(2,2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Переходя к полярным координатам x = r cos ϕ , |
|
y = r sin ϕ |
(или обоб- |
||||||||||||||||||||||||||||||||
|
щенным полярным координатам x = ar cosα ϕ , |
|
y = br sinα ϕ ), |
|
вычис- |
||||||||||||||||||||||||||||||
|
лить площадь области, ограниченной кривой |
|
x |
4 |
y |
|
|
|
x |
2 |
|
|
|
y |
2 |
|
3 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
5 = |
|
|
2 + |
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
a |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|||||
4. |
Найти объем тела az + x 2 |
≤ a 2 , 0 ≤ az ≤ 4a 2 |
− x 2 |
− y 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
5. |
Найти площадь поверхности cz = xy , если |
(x 2 |
+ y 2 )2 |
≤ 2c 2 xy , |
z ≥ 0 . |
|
|
||||||||||||||||||||||||||||
6. |
Записать |
∫∫∫ f (x, y, z)dxdydz |
интеграл в виде одного из повторных в |
||||||||||||||||||||||||||||||||
|
|
|
|
|
D |
|
|
|
D ={(x, y, z) : x2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
сферической системе координат, если |
+ y 2 + z 2 |
≥ R2 , |
||||||||||||||||||||||||||||||||
|
x 2 + y 2 + z 2 ≤ 2zR}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7. |
Записать |
∫∫∫ f (x, y, z)dxdydz в виде повторного интеграла, выбрав одну |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
из систем координат (декартову, цилиндрическую или сфериче- |
||||||||||||||||||||||||||||||||||
|
скую), если D = {(x, y, z) : |
|x + y | ≤ 2, 0 ≤ z ≤ 4 − x2 |
|
|
− y2 |
|
}. |
|
|
|
|
|
|
|
|
|
|
|
}. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
y |
2 |
|
2 |
|
z |
4 |
|
|
z |
|
||||
8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
+ |
|
|
|
|
|
+ |
|
|
= |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
4 |
|
|
|||||||||||
Найти объем тела, ограниченного поверхностью |
|
|
|
b |
|
|
c |
|
k |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
9.Найти массу шара радиусом R , если плотность его в каждой точке равна удвоенному расстоянию этой точки до поверхности шара.
10.Найти координаты центра тяжести однородной пластинки, занимающей область, ограниченную линиями: y = x, y = −x, x =1, если
плотность пластинки в каждой ее точке численно равна расстоянию от этой точки до начала координат.
11. |
Найти массу части конуса |
x2 + y2 = z 2 , |
0 ≤ z ≤ 4 , если плотность в |
||
|
каждой точке равна квадрату расстояния до вершины. |
|
|||
12. |
Вычислить |
поверхностный интеграл ∫∫ |
xdS , где S – часть цилинд- |
||
|
|
|
S |
|
|
|
ра x2 + y2 = 2ax , лежащая вне гиперболоида x2 + y2 − z 2 = a2 . |
|
|||
13. Вычислить |
поверхностный |
интеграл |
∫∫(xy + yz + zx)dS , |
где |
|
|
S = {(x, y, z) : z = x2 + y2 , x2 + y2 < 2ax}. |
S |
|
||
|
|
|
|||
8
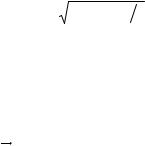
14. |
Вычислить криволинейный интеграл первого рода |
∫xyds , где L – |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
контур квадрата, ограниченного линиями x ± y =1, x ± y = −1. |
|||||||||||||||||
15. |
Вычислить криволинейный интеграл второго рода |
∫ydx −( y + x2 )dy , |
||||||||||||||||
|
где L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
– |
дуга |
параболы |
y = 2x − x2 |
от точки A = |
(2,1) |
до точки |
|||||||||||
16. |
B = (0,0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пользуясь формулой Стокса, вычислить ∫z 2 dx + x2 dy + y2 dz , где L – |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
кривая |
|
x2 +y2 = 2ax , |
|
z = |
(x2 + y2 ) 3 , положительно ориентирован- |
||||||||||||
|
ная на внешней стороне конуса. |
|
|
|
|
|
|
|
|
|||||||||
17. |
Вычислить |
поверхностный |
|
|
интеграл |
второго |
рода |
|||||||||||
|
∫∫(x + y2 )dydz + ( y + z 2 )dzdx + (z + x2 )dxdy , где S – часть внешней сторо- |
|||||||||||||||||
|
S |
|
|
+ y2 = a2 , 0 ≤ z ≤ H . |
|
|
|
|
|
|||||||||
|
ны цилиндра x2 |
|
|
|
|
|
||||||||||||
|
|
|
JG |
|
|
f (xyz) |
|
|
|
f (xyz) |
|
|
f (xyz) |
|
|
|
||
18. |
Найти |
div F , если F = |
|
i + |
|
j − 2 |
k , где i, j, k |
– единич- |
||||||||||
|
|
|
|
xz |
xy |
|||||||||||||
|
|
|
|
|
|
yz |
|
|
|
|
|
|
|
|
|
|||
|
ные орты, а f (u) |
– непрерывно дифференцируемая функция. |
||||||||||||||||
19. |
|
|
|
G |
G |
|
|
G |
|
G |
|
|
|
|
|
|||
Доказать, что div (F + Φ) = div F + div Φ . |
|
|
|
|||||||||||||||
20. |
Найти |
работу |
поля |
F = (2xy, x2 ) вдоль кратчайшей дуги эллипса |
||||||||||||||
|
x = a cos t, |
y = bsin t от точки A = (a,0) |
до точки B = (0,b) . |
|
||||||||||||||
21. |
Найти поток векторного поля |
F = 2xi + 2 yj − zk |
в направлении внеш- |
|||||||||||||||
|
ней нормали через поверхность S : x2 |
+ y2 = z 2 , |
0 ≤ z ≤ H . |
|
||||||||||||||
|
|
|
|
|
|
Вариант № 5 |
|
|
|
|
|
|||||||
1. |
В двойном интеграле |
|
∫∫ f (x, y)dxdy , где D = {(x, y) : | x −1| + | y |≤1}, пе- |
|||||||||||||||
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
рейти к полярным координатам r и ϕ , полагая x = r cos ϕ , |
y = r sin ϕ , |
||||||||||||||||
|
|
|
|
|
|
|
ϕ |
|
|
r |
(ϕ) |
|
|
|
|
|
||
|
и записать интеграл в виде |
∫2 |
dϕ |
2 |
∫g(r,ϕ)dr . |
|
|
|
||||||||||
|
|
|
|
|
|
|
ϕ1 |
|
|
r1 (ϕ) |
|
|
|
|
|
|||
2. Вычислить ∫∫xydxdy , где область D ограничена осями координат и
D
3. |
кривой x = a cos3 t, y = a sin 3 t, 0 ≤ t ≤π / 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Переходя к полярным координатам x = r cos ϕ , |
y = r sin ϕ |
(или обоб- |
||||||||||||||||||||||
|
щенным полярным координатам |
|
x = ar cosα ϕ , |
y = br sinα ϕ ), вычис- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
2 |
|
|
y |
2 |
3 |
|
|||
|
лить площадь области, ограниченной кривой |
|
|
x |
|
|
|
|
|
|
|
|||||||||||||
|
|
2 |
|
2 |
+ |
|
|
2 |
|
|
||||||||||||||
|
|
= |
|
|
|
. |
|
|||||||||||||||||
4. |
Найти объем тела x 2 ≤ az ≤ 4a 2 − x 2 |
− y 2 . |
|
|
|
|
c |
|
a |
|
|
|
b |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
|
2 |
3 |
2 |
|
4 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
c 2 |
|
|
5. |
Найти площадь поверхности (x |
|
+ y |
|
) = c |
|
z |
|
, если x |
|
|
+ y |
|
≤ |
|
. |
||||||||
|
|
|
|
|
|
|
16 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9

6. Записать ∫∫∫ f (x, y, z)dxdydz интеграл в виде одного из повторных в
D
сферической системе координат, если
|
D = {( x, y , z ) : x 2 + y 2 + z 2 ≤ R 2 , |
x 2 + y 2 + z 2 ≤ 2zR}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
7. |
Записать ∫∫∫ f (x, y, z)dxdydz , если |
D ={(x, y, z): x2 ≥ y2 +z2 , |
5x ≤ 4 +z2 + y2 } |
||||||||||||
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в виде повторного интеграла, выбрав одну из систем координат (де- |
||||||||||||||
|
картову, цилиндрическую или сферическую). |
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
2 |
|
y |
2 |
|
z |
2 |
|
xyz |
||||
|
|
x |
|
|
|
|
|
|
|
||||||
8. |
Найти объем тела, ограниченного поверхностью |
|
|
+ |
|
|
+ |
|
|
|
= |
|
|
|
|
|
2 |
|
2 |
|
2 |
|
3 |
|
|||||||
|
|
a |
|
|
b |
|
|
c |
|
|
|
h |
|
|
|
9. |
Найти массу сферического слоя между сферами |
x 2 |
+ y 2 |
+ z 2 |
= a 2 , |
||||||||||
x 2 + y 2 + z 2 = 4 a 2 , если плотность его в каждой точке обратно пропорциональна расстоянию точки от начала координат и на внешней сфере равна ρ0 .
10. Найти массу круглой пластинки радиусом R, если плотность пластинки в каждой точке пропорциональна расстоянию этой точки до центра пластины и равна ρ0 на краю пластины.
11. |
Найти статический момент части цилиндра |
x 2 + y 2 |
= 2 Ry , лежа- |
|||||
|
щей между плоскостями z = 0 и |
z = c , относительно плоскости XZ , |
||||||
|
если плотность ρ = y + z . |
|
|
|
|
|
||
12. |
Вычислить |
поверхностный интеграл ∫∫(x − y2 |
+ z 2 )dS , где S |
– часть |
||||
|
|
|
|
S |
|
|
|
|
|
цилиндра x2 |
+ y2 = a2 , x ≥ 0 , лежащая между плоскостями x + z = 0 и |
||||||
|
x − z = 0 . |
|
|
|
|
|
|
|
13. |
Найти координаты центра масс дуги однородной кривой L = {(x, y, z) : |
|||||||
|
x2 + y2 + z 2 = a2 , | y | = x, |
z ≥ 0}. |
|
|
|
|
|
|
14. |
Вычислить криволинейный интеграл первого рода |
∫xyds , где L – |
||||||
|
четверть окружности x2 |
|
|
|
L |
|
|
|
|
+ y2 =1, лежащая в первом квадранте. |
|
||||||
15. |
Вычислить криволинейный интеграл второго рода |
∫ydx −( y + x2 )dy , |
||||||
|
|
|
|
|
|
L |
|
|
|
где L – контур, составленный линиями y =0, y = x, y = |
1−x2 |
с поло- |
|||||
|
жительным направлением обхода. |
|
|
|
|
|||
16. |
Пользуясь формулой Стокса, вычислить |
|
|
|
|
|||
|
∫(z 2 − x2 − y)dx + ( y + z + x)dy + ( y + 2x + z3 )dz , где L – кривая |
x2 = y2 + z 2 , |
||||||
|
L |
|
|
|
|
|
|
|
|
x ≥ 0 , x2 +y2 + z 2 = 2az , положительно ориентированная на внешней |
|||||||
|
стороне правой x ≥ 0 полусферы. |
|
|
|
|
|
||
17. |
Вычислить |
поверхностный |
интеграл |
второго |
рода |
|||
|
∫∫x3dydz + y3dzdx + zdxdy , |
где S – |
часть внутренней стороны гипербо- |
|||||
|
S |
− z 2 =1, 0 ≤ z ≤ 3 . |
|
|
|
|
|
|
|
лоида x2 + y2 |
|
|
|
|
|
||
10
