5 _теория вероятностей

Методические рекомендации для студентов 1 курса факультета по РИУ по специальности «лечебное дело»

по самоподготовке к практическому занятию по математике

Тема: Основные понятия теории вероятностей. Теоремы теории вероятностей. Повторные независимые испытания.

Актуальность темы: ознакомление с основными понятиями и методами теории вероятностей как средства решения задач физического, химического, биологического и иного характера, встречающихся как в процессе изучения профильных дисциплин, так и в дальнейшей профессиональной деятельности

Цель занятия: научиться решению задач на вычисление вероятности событий с использованием классического и статистического определения вероятности, теоремы сложения вероятностей событий, теоремы умножения вероятностей событий, формулы полной вероятности, формулы Байеса, формулы Бернулли и Пуассона.

План изучения темы

1.Понятие испытания, события; достоверные невозможные, невозможные, случайные события.

2.Классическое определение вероятности события. Статистическое определение вероятности событий.

3.Теорема сложения вероятностей и следствия из нее.

4.Теорема умножения вероятностей и следствия из нее.

5.Формула полной вероятности. Формула Байеса.

6.Формула Бернулли. Формула Пуассона.

Рекомендуемая литература:

Основная литература:

1.Морозов, Ю.В. Основы высшей математики и статистики: учеб. для студентов мед. и фаpмацевт. вузов и фак./Ю.В. Морозов.-

М.:Медицина, 2004.-232 с.

2.Основы высшей математики и математической статистики: учеб. для студентов мед. и фармацевт. вузов/И.В. Павлушков,

Л.В.Розовский, А.Е.Капульцевич и др.-2-е изд., испр.-М.:ГОЭТАР-

Медиа, 2006.-423 с.

Дополнительная литература:

∙Методические рекомендации к практическим занятиям по высшей математике [Электронный ресурс]: учеб.-метод. пособие для вузов/ авт.-сост. : Т.А.Новичкова; ГОУ ВПО "Курск. гос. мед. ун-т", каф. физики, информатики и математики.-Курск:КГМУ, 2009.

∙ Гмурман В.Е. Теория и математическая статистика. М. «Высшая школа», изд. 5, 2004.

Вопросы для самоконтроля:

1.Что понимают под испытанием?

2.Что такое событие?

3.Какое событие называют достоверным, невозможным, случайным? Приведите примеры.

4.Какое событие называется совместимым, несовместимым, случайным? Приведите примеры.

5.Что понимают под полной группой событий? Примеры.

6.Какие события называются равновозможными? Примеры.

7.Что понимают под элементарными событиями или случаями?

8.Приведите классическое определение вероятности события.

9.Чему равна вероятность достоверного, невозможного, случайного

события?

10.Что такое частота и относительная частота события?

11.Как статистически определить вероятность события?

12.Что понимают под суммой двух событий?

13.Сформулируйте теорему сложения вероятностей несовместимых

событий.

14.Что понимают под произведением двух событий?

15.Какие события называются зависимыми, независимыми? Приведите примеры.

16.Что называют условной вероятностью события?

17.Сформулируйте теорему умножения вероятностей для независимых и зависимых событий.

18.Сформулируйте теорему сложения вероятностей совместимых

событий.

19.Что понимают под полной группой событий? Примеры.

20.Какие события называются равновозможными? Примеры.

21.Что понимают под элементарными событиями или случаями?

22.Чему равна вероятность достоверного, невозможного, случайного

события?

23.Что понимают под суммой двух событий?

24.Что понимают под произведением двух событий?

25.Что называют условной вероятностью события?

26.Сформулируйте теорему о полной вероятности.

27.Запишите формулу Байеса.

28.Какие события называются зависимыми, независимыми? Приведите примеры.

29.Запишите формулу Бернулли.

30.Запишите и сформулируйте локальную теорему Лапласа.

31.Запишите и сформулируйте интегральную теорему Лапласа.

32.Формула вероятности отклонения относительной частоты события от его вероятности.

33.Запишите и сформулируйте теорему Пуассона.

Задания на самоподготовку:

1.В урне 3 белых и 7 черных шаров. Наугад извлекается 1 шар. Найти вероятность того, что он будет белым.

2.Имеется два набора ампул. Вероятность того, что ампула первого набора пятиграммовая, равна 0,8, а второго-0,9. Найти вероятность того, что взятая наудачу ампулапятиграммовая

3.На 7 карточках напечатаны буквы, образующие слово СОЛОВЕЙ. Карточки перемешивают и из них наугад последовательно извлекают слева направо 5 карточек. Найти вероятность того, что получится слово СЛОВО.

4.В сельской библиотеке 2500 книг. Из них приключенческих 790, научно-популярных журналов 250, исторических 780, детских 680. Вероятность того, что книга издана после 2000 года соответственно равна 0,78, 0,65, 0,54, 0,35. Найти вероятность того, что читатель закажет книгу, изданную после 2000 года.

5.На склад аптечного киоска привезли 100 упаковок лекарственных средств. Из них 25 – анальгин, 36 – парацетамол, 39 – аспирин. Известны вероятности того, что указанные лекарственные средства удовлетворяют ГОСТу соответственно 0,98, 0,95, 0,97. Найти вероятность того, что извлеченное лекарственное средство, удовлетворяет ГОСТу и является парацетамолом.

Ориентировочные основы действий:

1.Изучить основные понятия по теме

2.Ответить на вопросы для самоконтроля

3.Проработать примеры решения задач по теме

4.Выполнить задания для самостоятельного контроля

5.Решить контрольные задания по теме

После изучения данной темы студент должен знать: основные понятия теории вероятностей: событий случайных,

достоверных, невозможных, совместных и несовместных событий, равновозможных событий, зависимых и независимых событий; классического и статистического определения вероятности.

уметь: применять теоремы сложения, умножения вероятностей, теоремы о полной вероятности, формулу Байеса, формулу Бернулли для решения задач.

Множество {1,2,3}. Составить все возможные размещения из элементов данного множества по два.

Размещения по два (1,2), (2,1), (2,3), (3,2), (3,1), (1,3)

Теорема 3 (о числе размещений)

Число всех размещений из n элементов по k определяется формулой

Пример 5.

Расписание одного дня занятий состоит из пяти уроков. Определить число вариантов расписания 1 дня, если всего 11 дисциплин.

Так как важен порядок уроков и составляем наборы из 11 по 5, то имеем дело с размещениями из 11 элементов по 5.

Неупорядоченные наборы из n элементов по k называются сочетаниями из n

элементов по k.

Пример 6.

Множество {1,2,3}. Составить все возможные сочетания из элементов данного множества по два.

Сочетания по два (1,2), (2,3), (3,1).

Теорема 4 (о числе сочетаний)

Число всех сочетаний из n элементов по k определяется формулой

Коэффициенты Сnk называются биномиальными, т.к. они входят в формулу

n

бинома Ньютона (a + b)n = ∑Cnk a k bn−k .

k =0

Например, (a + b)2 = C20 a0b2−0 + C21a1b2−1 + C22 a2b2−2 = b2 + 2ab + a2 .

Пример 7.

В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна 1 партия.

Все 16 играют по два, причем не важно Коля с Васей играет или Вася с Колей.

Следовательно, число партий в турнире – число сочетаний из 16 элементов по два.

Если в размещениях (сочетаниях) из n элементов по k некоторые из элементов или все могут оказаться одинаковыми, то такие размещения (сочетания) называют размещениями (сочетаниями) с повторениями из n элементов по k.

Число размещений с повторениями из n элементов по k.

A~nk = nk

Число сочетаний с повторениями из n элементов по k.

C~nk = Cnk+k −1

Теория вероятностей

Случайные события и их классификация

Испытание – осуществление некоторого определенного комплекса условий, который может быть повторен сколь угодное число раз.

Событие – любой результат или исход испытания.

Обозначение: прописными буквами латинского алфавита – A, B, C…

События делятся на три вида: достоверные, невозможные, случайные. Достоверное событие – событие, которое в результате испытания обязательно произойдет.

Невозможное событие – событие, которое в результате испытания не может произойти.

Случайное событие – событие, которое в результате испытания может произойти либо не произойти.

Два события называются совместными, если в результате одного испытания наступление одного из них не исключает наступления другого.

Два события называются совместными, если в результате одного испытания наступление одного из них исключает наступление второго.

Случайные события образуют полную группу событий, если при каждом испытании может осуществиться событие только из этой группы и не может осуществиться любое несовместное ним.

События называются равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

События, образующие полную группу равновозможных событий,

называются элементарными событиями (исходами).

Те элементарные исходы, в которых интересующее нас событие наступает, называются благоприятствующими этому событию.

Два события называются противоположными, если они несовместны и образуют полную группу.

Обозначение: событие А, ему противоположное Ā.

Классическое определение вероятности.

В практической деятельности важно уметь сравнивать события по степени возможности их наступления. Поэтому для сравнения нужна определенная мера.

Численная мера степени объективной возможности наступления события называется вероятностью события.

Согласно классическому определению вероятностью P(A) события А называется отношение числа m благоприятствующих этому событию исходов к общему числу n всех элементарных (т.е. всех возможных, несовместных) исходов (образующих полную группу).

P( A) = m n

Пример 8.

В корзине 2 белых и 8 черных шаров. Наугад извлекается 1 шар. Найти вероятность того, что он будет белым.

События равновозможны, несовместны, образуют полную группу, следовательно имеет место классическая схема определения вероятности.

Событие А – извлечение белого шара. N=10, m=2.

P( A) = m = 2 = 0,2 n 10

Пример 9.

Какова вероятность угадать 6 цифр в лотерее?

Общее число способов отобрать 6 цифр из 49 - С496 .

Свойства вероятности

1)0≤p≤1;

2)P(Ø)=0, Ø – невозможное событие;

3)P(Ω)=1, Ω – достоверное событие.

Статистическое определение вероятности.

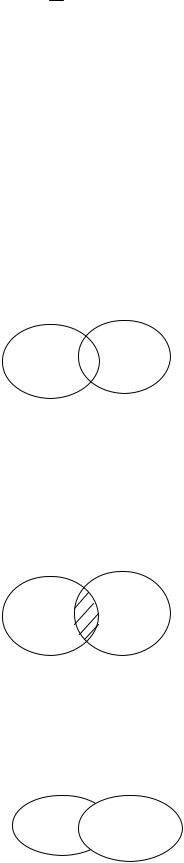
Если в n наблюдениях (испытаниях) событие А наступило m раз, то

отношение m = w(A) называется относительной частотой (частотой)

n

события А.

Статистический вероятностью события А называется предел отношения относительной частоты при стремлении числа испытаний к

Отличие классического определения вероятности от статистического в том, что классическое определение не требует, чтобы испытания проводились в действительности.

Действия над событиями

Суммой событий А и В называется событие С, заключающееся в

наступлении хотя бы одного из событий А и В.

C = A + B = A B

B

A

Если события А и В – совместны, событие С заключается в наступлении или А, или В, или А и В одновременно.

Если события А и В – несовместны, событие С заключается в наступлении или А, или В.

Произведением событий А и В называется событие С, состоящее в одновременном наступлении событий.

C = A × B = A Ç B

A B

Если события А, В, D – совместны, событие С заключается в одновременном наступлении всех трёх событий.

Если события А и В – несовместны, событие С - невозможное.

Разностью событий А-В называется событие С, которое заключается в том, что событие А наступило, а событие В – нет.

A

B

Теорема сложения вероятностей

Вероятность суммы двух событий А и В равна сумме вероятностей этих событий минус вероятность их совместного наступления.

P(A+B)=P(A)+P(B)-P(AB)

Пример 10.

Из 100 студентов, находящихся в аудитории, 50 человек знают английский язык (событие А), 40 – французский (событие В), 35 – немецкий (событие С). Английский и французский знают 20 человек, английский и немецкий – 8. Все три языка знают 5 человек. Один из студентов вышел. Определить вероятности следующих событий:

а) знает английский или немецкий языки, б) кроме английского языка, знает немецкий или французский языки.

а) P( A + C) = P( A) + P(C) − P( AC) = 0.5 + 0.35 − 0.08 = 0.77

б) P( AC + AB) = P( AC) + P( AB) − P( ABC) = 0.08 + 0.2 − 0.05 = 0.23

Следствия:

1. Для n несовместных событий A1, A2, …, A n

P(A1+ A2+ …+ A n)=P(A1)+P(A2)+ …+P(An)

2. Для полной группы событий

P(A1+ A2+ …+ An)=1

3. Для противоположных событий

P(A)+P(Ā)=1

Теорема умножения вероятностей

Вероятность наступления события В, зависящая от наступления события А называется условной вероятностью события В.

PA(B)=P(B/A)

Два события называются независимыми, если вероятность осуществления одного из них не зависит от наступления другого.

Теорема.

Вероятность произведения двух событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие произошло.

P(AB)=P(A)P(B/A)= P(B)P(A/B)

Следствия:

1. Для независимых событий

P(A1·A2)=P(A1)·P(A2)

2. Для n событий A1, A2, …, An

P(A1 A2 ×...× An ) = P(A1 )PA1 (A2 )PA1 A2 (A3 )×...× PA1 A2 ...An−1 (An )

Т.е. вероятность произведения нескольких событий равна произведению вероятности независимого события на условные вероятности других, причем условная вероятность каждого последующего вычисляется в предположении, что все предыдущие уже наступили.

Пример 11.

На 7 карточках напечатаны буквы слова «СОЛОВЕЙ». Карточки перемешивают и из них наугад последовательно извлекают, выкладывая слева направо, 3 карточки. Найти вероятность того, что получится слово

«ВОЛ».

Событие А – на 1й карточке «В», Событие В – на 2й карточке «О», (первая В)

Событие С – на 3й карточке «Л», (первая В, вторая О)

Формула полной вероятности

Пусть событие А может произойти при условии наступления одного из событий В1, В2, …, Вn.

n

Тогда P( A) = ∑ P(Bi )P(A / Bi ) = P(B1 )P(A / B1 ) + P(B2 )P(A / B2 ) + ... + P(Bn )P(A / Bn )

i=0

Пример 12.

Вероятность брака при изготовлении детали равна 0,04. Приемка деталей производится по следующей системе контроля: годная деталь принимается с вероятностью 0,98, а бракованна – с вероятностью 0,1. Найти вероятность приемки детали.

Событие А – изготовленная деталь принята.

P(A/ B1)=0.98 вероятность того, что принятая деталь – хорошая P(A/ B2)=0.1 вероятность того, что принятая деталь – бракованная

Вероятность того, что деталь будет принята

P( A) = P(B1 )P(A / B1 )+ P(B2 )P(A / B2 ) = 0.96 * 0.98 + 0.04 * 0.1 = 0.9448

Пример 13.

Имеются три одинаковых ящика с шарами. В первом ящике 30 белых и 20 черных шаров, во втором – 15 белых и 15 черных шаров, в третьем – 5 белых и 15 черных шаров. Какова вероятность вытащить из случайно выбранного ящика черный шар.