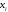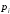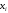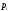- •Лекція 7: Основні поняття теорії ймовірностей.
- •1. Предмет теорії ймовірностей. Випробування, події, класифікація подій.
- •2.1. Класичне і статистичне означення ймовірності
- •2.2. Статистичне означення ймовірності.
- •Сума і добуток двох подій, їх властивості
- •4. Повторні незалежні випробування. Схема Бернуллі.
- •4.2. Формула Бернуллі.
- •4.4. Інтегральна формула Муавра-Лапласа
- •4.5. Ймовірність відхилення відносної частоти успіху.
- •4.6. Формула Пуассона
- •4.7. Простий потік подій
4.6. Формула Пуассона
Ймовірність
того, що в n
незалежних
випробуваннях, в кожному з яких ймовірність
появи події дорівнює
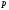 (
(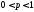 ),
подія настане рівноk
разів
(без різниці, в якій послідовності),
обчислюється: за наближеною
формулою
Пуассона:
),
подія настане рівноk
разів
(без різниці, в якій послідовності),
обчислюється: за наближеною
формулою
Пуассона:
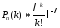 ,
де k=
0; 1; 2; ...; n;
,
де k=
0; 1; 2; ...; n;
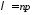 – середня кількість успіхів
(появи
події А);
– середня кількість успіхів
(появи
події А);
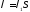 –добуток
середньої кількості появи подій на
розмір області (одиниця області: площі,
об’єму, часу).
–добуток
середньої кількості появи подій на
розмір області (одиниця області: площі,
об’єму, часу).
Примітка: ймовірність р появи події А в одному випробуванні дуже мала (говорять, що подія А-рідкісна), кількість випробувань n „велика” і добуток np<10, тоді застосовуємо формулу Пуассона.
Приклад №1. Завод відправив на базу 4000 якісних виробів. Імовірність того, що в дорозі виріб пошкодиться, дорівнює 0,00025. Знайти ймовірність того, що на базу надійде: 1) 5 пошкоджених виробів; 2) принаймні один пошкоджений виріб; 3) не менше двох пошкоджених виробів; 4) не більше одного пошкодженого виробу.
Розв’язання.
Випробування
полягають у
транспортуванні
виробів на базу. Подія А – при
транспортуванні виріб пошкодився.
Оскільки добуток
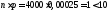 ,
то за формулою Пуассона маємо:
,
то за формулою Пуассона маємо:
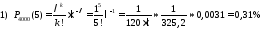 ;
;
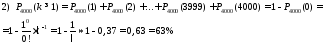 ;
;
 ;
;
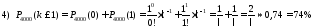
Відповідь: 1) 0,31%; 2) 63%; 3) 26,2%; 4) 74%.
4.7. Простий потік подій
Часто події, що розглядаються при розв’язуванні виробничих задач, настають у випадкові моменти часу. Тоді потоком (течією) подій називають послідовність таких подій, які наступають у випадкові моменти часу. Наприклад: заяви до диспетчерського пункту з викликом таксі; виклики на АТС пункту швидкої медичної допомоги; послідовність відмов елементів у електричному ланцюзі і т.д.
Потік називається простим пуассонівським, якщо виконуються умови:
стаціонарний, тобто залежить від кількості
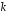 появ події та часу
появ події та часу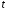 (ймовірності появи
(ймовірності появи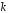 подій за проміжок часу
подій за проміжок часу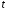 рівні між собою) і не залежить від
моменту свого початку;
рівні між собою) і не залежить від
моменту свого початку;має властивість відсутності післядії, тобто ймовірність появи події не залежить від появи або не появи події раніше та не впливає на найближче майбутнє;
ординарний, тобто ймовірність появи більше однієї події в малий проміжок часу є величина нескінченно мала у порівнянні з імовірністю появи події один раз у цей проміжок часу (за нескінченно малий проміжок часу може з’явитись не більше однієї події).
Середня
кількість
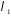 появ подійА
в одиницю часу називається інтенсивністю
потоку.
появ подійА
в одиницю часу називається інтенсивністю
потоку.
Твердження:
якщо
потік подій пуасонівський, то ймовірність
появи події А
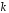 разів за час
разів за час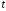 обчислюється за формулою:
обчислюється за формулою: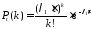 ,
де
,
де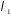 – інтенсивність потоку. Цю формулу
іноді називаютьматематичною
моделлю простого потоку подій.
– інтенсивність потоку. Цю формулу
іноді називаютьматематичною
моделлю простого потоку подій.
Приклад № 2. Всередньому на 1м2 площі посіву зустрічається 0,5 стеблин бур’яну. Знайти ймовірність того, що на площі 4м2 знайдеться: 1) 2 стеблини бур’янів; 2) не більше двох стеблин бур’янів; 3) принаймні одна стеблина бур’яну.
Розв’язання.
Випробування
полягають у дослідженні посівів на
наявність бур’янів.
Подія А
– на площі посівів знайшлися стеблини
бур’янів.
Кожна
стеблина бур’яну розглядається як
точка, яка з’являється в заданій площі.
Застосовуємо формулу Пуассона. За умовою
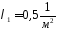 ,
s=4м2
(це
середня кількість подій, у нашому випадку
– стеблин бур’янів,
які з’являються
на одиниці площі).
Параметр розподілу Пуассона =1s=0,54=2.
Шукану
ймовірність
знаходимо за формулою Пуассона:
,
s=4м2
(це
середня кількість подій, у нашому випадку
– стеблин бур’янів,
які з’являються
на одиниці площі).
Параметр розподілу Пуассона =1s=0,54=2.
Шукану
ймовірність
знаходимо за формулою Пуассона:
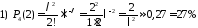 ;
;
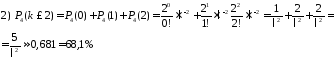 ;
;
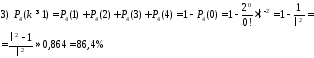 .
.
Відповідь: 1) 27%; 2) 68,1%; 3) 86,4%.
Приклад № 3. Рукопис об’ємом 1000 сторінок друкованого тексту містить 1000 помилок, допущених при наборі (опечаток). Знайти ймовірність того, що навмання взята сторінка містить: 1) хоча б одну опечатку; 2) рівно 2 опечатки; 3) не менше двох опечаток; 4) не більше однієї опечатки. (Вважати, що кількість опечаток розподілена за законом Пуассона).
Розв’язання.
Параметр
розподілу Пуассона:
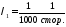 .
.
Маємо
простий потік подій із інтенсивністю
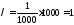 ,
тоді за формулою:
,
тоді за формулою:
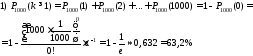 ;
;
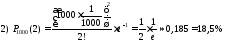 ;
;
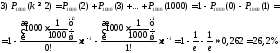 ;
;
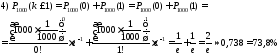
Відповідь: 1) 63,2%; 2) 18,5%; 3) 26,2%; 4) 73,8%.
Найімовірніше число.
Розглянемо приклад: нехай підкинули монету 4 рази. Подія А полягає у появі герба. Складемо таблицю в якій у першому рядку фіксуватимемо кількість гербів при 4 підкиданнях (0 – ні разу не випав герб, 1 – один раз випав герб, і т.д.). Ймовірність появи герба при кожному підкиданні стала і рівна ½, тоді неуспіх – цифра – ½.
|
|
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
Визначимо при якій кількості підкидань монетки герб з’являтиметься найчастіше?
У другому рядку таблиці запишемо обчислені ймовірності появи у кожному із 4 підкидань герба:
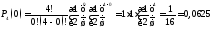 ;
;
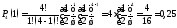 ;
;
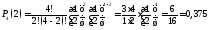 ;
;
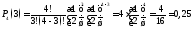 ;
;
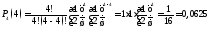 .
.
Заповнимо другий рядок таблиці:
|
|
0 |
1 |
2 |
3 |
4 |
|
|
0,0625 |
0,25 |
0,375 |
0,25 |
0,0625 |
Причому,
звернемо увагу:
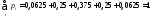
При
фіксованому n
= 4 імовірності
 спочатку зростають при збільшенні числаk
від
0 до деякого числа
спочатку зростають при збільшенні числаk
від
0 до деякого числа
 (у даному випадку це 2), і починають
спадати при подальшому збільшенні числаk.
Кількість
успіхів
(у даному випадку це 2), і починають
спадати при подальшому збільшенні числаk.
Кількість
успіхів
 ,
якій відповідає найбільша ймовірність
,
якій відповідає найбільша ймовірність
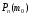 ,
називаютьнайбільш
імовірною кількістю успіхів,
або найімовірнішим
числом,
або модою.
Її визначають із нерівності:
,
називаютьнайбільш
імовірною кількістю успіхів,
або найімовірнішим
числом,
або модою.
Її визначають із нерівності: 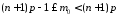 ,
або
,
або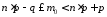
Якщо:
число
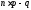 – ціле, то існують дві моди, а саме
– ціле, то існують дві моди, а саме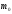 і
і ;
;число
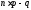 – дробове, то існує одна мода, а саме
– дробове, то існує одна мода, а саме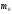 ;
;якщо число
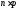 – ціле, то мода визначається, як
– ціле, то мода визначається, як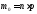 .
.
Обчислимо аналітично: n=4, р=0,2, тоді:
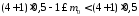
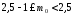 ,
,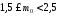
Ціле число (кількість підкидань), що міститься між даними і буде модою – 2.
Приклад № 3. Садівник зробив восени 6 прививок. Із досвіду минулих років відомо, що після зимування 7 із кожних 10 черенків залишаються життєздатними. Яка найбільш імовірна кількість життєздатних черенків?
Розв’язання.
Випробування
полягають у тому, що садівник восени
висаджує черенки. Подія А – черенок
перезимував і залишився життєздатним.
За умовою
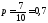 – ймовірність життєздатності черенків.
– ймовірність життєздатності черенків.
За
формулою:
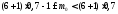 або
або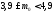 ,
тобто
,
тобто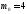 .
.
Відповідь: найбільш імовірна кількість черенків, які „приживуться” рівна 4.
Приклад № 4. Скільки треба виконати незалежних випробувань із ймовірністю появи події у кожному виробуванні, рівною 0,4, щоб найімовірніше число появи події у цих випробуваннях було рівне 25?
Розв’язання.
За
умовою
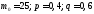 .
Застосуємо формулу:
.
Застосуємо формулу: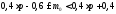 ,
виконаємо спрощення:
,
виконаємо спрощення: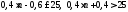 .
Отримаємо результат:
.
Отримаємо результат: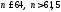 .
Тобто шукана кількість випробувань
повинна задовільняти подвійну нерівність:
.
Тобто шукана кількість випробувань
повинна задовільняти подвійну нерівність: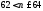 ,
це, зрозуміло, що
,
це, зрозуміло, що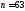 .
.
Відповідь: 63.
Приклад
№ 5. Знайти
ймовірність
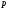 появи події у кожному із 49 незалежних
випробувань, якщо найімовірніше число
настання події у цих випробуваннях
дорівнює 30.
появи події у кожному із 49 незалежних
випробувань, якщо найімовірніше число
настання події у цих випробуваннях
дорівнює 30.
Розв’язання.
За
умовою
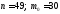 .
Застосуємо формулу:
.
Застосуємо формулу: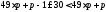 та виконаємо спрощення:
та виконаємо спрощення: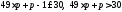 або
або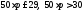 .
Таким чином
.
Таким чином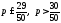 або
або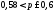 – нерівність задає проміжок, якому
належить шукане значення ймовірності.
– нерівність задає проміжок, якому
належить шукане значення ймовірності.
Відповідь:
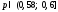 .
.