
- •Лекція 7: Основні поняття теорії ймовірностей.
- •1. Предмет теорії ймовірностей. Випробування, події, класифікація подій.
- •2.1. Класичне і статистичне означення ймовірності
- •2.2. Статистичне означення ймовірності.
- •Сума і добуток двох подій, їх властивості
- •4. Повторні незалежні випробування. Схема Бернуллі.
- •4.2. Формула Бернуллі.
- •4.4. Інтегральна формула Муавра-Лапласа
- •4.5. Ймовірність відхилення відносної частоти успіху.
- •4.6. Формула Пуассона
- •4.7. Простий потік подій
2.2. Статистичне означення ймовірності.
Відносною частотою події А називають відношення числа m випробувань, в яких подія А мала місце до загального числа фактично проведених випробувань n. Тобто: W(А) = m / n.
Означення відносної частоти припускає, що випробування були проведені фактично, тобто ймовірність обчислюється до експерименту, а відносна ймовірність – після експерименту.
Приклад
№ 4:
відділ технічного контролю продукції
виявив 5 нестандартних деталей в партії
з 60 випадково відібраних деталей. Тоді
відносна частота появи нестандартної
деталі: 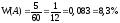 .
.
Якщо проводити експеримент в однакових умовах, у кожному з яких число випробувань достатньо велике, то відносна частота стає стійкою, коливаючись навколо деякого сталого числа, яке можна вважати за наближене значення ймовірності, яке називається статистичною ймовірністю.
Властивості ймовірності:
Ймовірність будь-якої події А задовольняє нерівність: 0 ≤ Р(А) ≤ 1.
Ймовірність достовірної події дорівнює 1. Аналогічно неможливої – 0.
Для
незалежних подій А
і В
виконуються рівності:
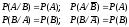 .
.
На практиці висновок про незалежність тих чи інших подій роблять виходячи з інтуїтивних міркувань і аналізу умов випробування, вважаючи незалежними ті події, між якими немає причинних зв’язків.
Сума і добуток двох подій, їх властивості
Сумою двох подій А і В називається така подія С = А+В, яка відбувається тоді і тільки тоді, коли відбувається принаймні одна з подій А або В.
Приклад № 5: у корзині 6 білих, 4 червоних, 7 зелених і 2 голубих кульки. Після того, як їх ретельно перемішали, взяли навмання одну з них. Яка ймовірність того, що кулька кольорова?
Події:
А
– взяли білу кульку, В
– взяли червону, С
– взяли зелену, D
– взяли голубу. За умовою нас цікавить
поява червоної, або зеленої, або голубої
кульок (будь-якого кольору, тільки не
білу):
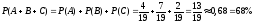 .
.
Добутком двох подій А і В називається така подія С = А·В, яка відбувається тоді і тільки тоді, коли події А і В відбуваються разом (одночасно).
Сума ймовірностей подій, які утворюють повну групу подій дорівнює 1.
Розглянемо властивості ймовірностей сумісних, залежних та інших видів подій:
1) Ймовiрність
суми двох сумісних,
незалежних
подій дорівнює сумі ймовiрностей
цих подій без ймовiрності
їх добутку:
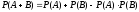 .
.
2) Ймовірність
суми двох сумісних,
залежних
подій дорівнює сумі ймовірностей цих
подій без умовної ймовірності першої,
обчисленої в припущенні, що відбулась
друга:
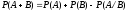 .
.
3) Ймовiрність
суми несумісних
подій дорівнює сумі ймовiрностей
цих подій:
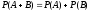 .
.
4) Ймовiрність
добутку двох залежних
подій дорівнює добутку ймовiрності
однієї з них на ймовiрність
іншої при умові, що відбулась перша
подія:
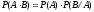 .
.
5) Ймовiрність
добутку незалежних
подій
дорівнює добутку ймовiрностей
цих подій:
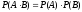 .
.
Приклад № 6: у тролейбусному парку п’ять машин №1 і три машини №2. Яка ймовiрність, що перші дві машини, які вийшли з парку, мають № 1?
Розв'язання. Позначимо події: А – перша машина має №1; В – друга машина має №1; С – перші дві машини мають №1. Тоді Р(А) = 5/8. Якщо відомо, що подія А відбулася, то в парку залишилось чотири машини №1 і три машини №2, тобто події А і В – залежні, оскільки ймовірність появи події В залежить від появи події А. Тому:
Р(В/А) = 4/7. Отже, Р(С) = Р(АВ) = Р(А)Р(В/А) = 5/8·4/7 = 20/56 = 0,357 = 35,7%.
Відповідь: 35,7%.
Приклад № 7: Ймовiрність влучення з однієї гармати 0,85, а з другої – 0,7. Знайти ймовiрність принаймні одного влучення при залпі з двох гармат.
Розв'язання. Позначимо події: А – влучила перша гармата; В – влучила друга гармата; С – принаймні одне влучення. Зрозуміло, що А і В – сумісні, незалежні події.
Перший
спосіб: 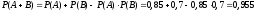 .
.
Другий
спосіб.
Події
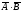 – протилежні, тобто
– протилежні, тобто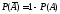 – ймовірність невлучення в ціль першою
гарматою. Аналогічно
– ймовірність невлучення в ціль першою
гарматою. Аналогічно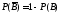 .
Тоді протилежною подією до „принаймні
одного влучення
при залпі з двох гармат”
буде подія ніодного влучення при залпі
з двох гармат:
.
Тоді протилежною подією до „принаймні
одного влучення
при залпі з двох гармат”
буде подія ніодного влучення при залпі
з двох гармат:
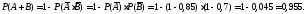
Третій спосіб. Розглянемо можливі випадки подій при умові „принаймні одного влучення”: можливі випадки, що влучили з обох гармат одночасно, або з першої гармати влучили, а з дугої – ні, або з першої не влучили, а з другої гармати влучили, тобто маємо:
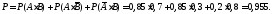
Відповідь: 95,5%.
Формула повної ймовірності, ймовірність гіпотез.
3.1. Формули повної ймовiрності.
Нехай
подія В може відбутися лише разом з
однією із подій (гіпотез): Н1,
Н2,
Н3,
..., Нn
,
які є несумісні і утворюють повну групу
подій, тобто
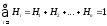 .
.
Тоді: Р(А) = Р(Н1)Р(А/Н1) +...+ Р(Нn)Р(А/Нn)
Ця формула називається формулою повної ймовiрності, де події Н1,..., Нn – гіпотези.
Приклад № 8: Штампувальний цех направив у відділ технічного контролю дві партії деталей. Перша партія містить 30000 деталей, 5% з яких браковані. Друга партія містить 20000 деталей з 1% браку. Деталі обох партій надходять на спільний конвейєр для перевірки контролером. Контролер навмання взяв одну деталь. Яка ймовірність що деталь бракована?
Розв'язання. Позначимо події: А – деталь бракована; гіпотези: Н1 – деталь із першої партії; Н2 – деталь із другої партії. Тоді, за умовою задачі:
Ймовірність
випадкового вибору деталі з першої
партії:
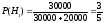 ;
аналогічно з другої
;
аналогічно з другої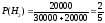 .
.
Умовні
ймовірності ( – ймовірність випадково вибраної
бракованої деталі, з першої партії,
аналогічно
– ймовірність випадково вибраної
бракованої деталі, з першої партії,
аналогічно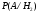 з другої). Тобто:
з другої). Тобто: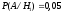 і
і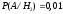 .
.
За формулою повної ймовiрності необхідно обчислити ймовірність того, що навмання взята деталь бракована (незалежно від того, з якої вона партії):
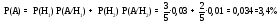
Відповідь: ймовірність вибору з конвейєра бракованої деталі контролером складає 3,4%.
3.2. Формула Байєса.
В
умовах формули повної ймовiрності, можна
переоцінити ймовiрності гіпотез за
формулами
Байєса:
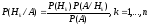
Приклад № 8: Два верстата-автомата виробляють однакові деталі, які надходять на спільний конвейєр. Продуктивність першого верстата в 4 рази вища за продуктивність другого. Перший верстат в середньому виробляє 30% деталей відмінної якості, а другий – 80%. Навмання взята деталь виявилася відмінної якості. Знайти ймовiрність, що цю деталь виготовлено на другому верстаті.
Розв'язання. Позначимо події: А – деталь відмінної якості; Н1 – деталь виготовлено на першому верстаті; Н2 – деталь виготовлено на другому верстаті. Тоді, за умовою задачі:
Р(Н1) = 4/5 = 0,8; Р(А/Н1) = 30/100 = 0,3;
Р(Н2) = 1/5 = 0,2; Р(А/Н2) = 80/100 = 0,8;
За формулою повної ймовiрності
Р(А) = Р(Н1)Р(А/Н1) + Р(Н2)Р(А/Н2) = 0,8·0,3 + 0,2·0,8 = 0,4.
За формулою Байєса: Р(Н2/A) = Р(Н2)Р(А/Н2) / P(A) = 0,2·0,8/0,4 = 0,4.
Одержаний результат можна розуміти таким чином: серед деталей відмінної якості 40% складають деталі, які виготовлені на другому верстаті.
Відповідь: 40%.
Приклад № 10: У телевізійному ательє є 4 кінескопи. Ймовірності того, що кінескопи витримують гарантійний термін служби, відповідно дорівнюють 0,8; 0,85; 0,9 і 0,95. Знайти ймовірність того, що взятий навмання кінескоп витримає гарантійний термін служби.
Розв'язання. Позначимо події: А – кінескоп витримав гарантійний термін служби; Н1 – перший кінескоп витримав гарантійний термін служби; Н2 – другий кінескоп витримав гарантійний термін служби; Н3 – третій і Н4 – четвертий. Тоді, за умовою задачі
Р(Н1) = 1/4 = 0,25; Р(А/Н1) = 0,8;
Р(Н2) = 1/4 = 0,25; Р(А/Н2) = 0,85;
Р(Н3) = 1/4 = 0,25; Р(А/Н1) = 0,9;
Р(Н4) = 1/4 = 0,25; Р(А/Н2) = 0,95.
За формулою повної ймовiрності:
Р(А) = Р(Н1)Р(А/Н1) + Р(Н2)Р(А/Н2) + Р(Н3)Р(А/Н3) + Р(Н4)Р(А/Н4) = 0,25·0,8 + 0,25·0,85 + 0,25 0,9 + 0,25 0,95 = 0,875 = 87,5 %.
Відповідь: ймовірність того, що взятий навмання кінескоп витримає гарантійний термін служби 87,5%.
