36. Однопродуктовая транспортная задача в матричной постановке.

Есть m поставщиков и n потребителей одно­родного товара. Поставщик i характеризуется мощностью a_i

b_j- потребность потребителя j

c_ij- затраты на поставку

Задача - распределить товар с min-ми суммар­ными затратами

x_ij- объем поставки

-суммарная поставка потребителю j

-суммарный вывоз от поставщика i

мощность пр-ва товара должна быть больше, чем он поставляет

минимизируем затраты

Задача имеет решение тогда и т.т., когда она совместна и ограничена

Совместность:

Предлож-е i, спрос j. Поставка больше спроса, но меньше предло­жения поставщика

Суммарное наличие не меньше суммарной потребности

если достигается равенство, задача называется замкнутой, сбалансирован­ной

Если задача не сбалансирована, у какого-то поставщика будет излишек

Надо ввести фиктивного потребителя (n+1), который будет проглатывать излишек и задача становится сбалансированной:

С_i,n+1 – ущерб от избыточной единицы

Если задача несовместна

то надо вводить фиктивного поставщика m+1

Его мощность

C_m+1,j – ущерб потребителя j от недопоставки единицы товара

37. Основные предпосылки и методика применения мнк.

При оценке параметров уравнения регрессии применяется МНК. Этот метод дает возможность при заданном виде зависимости переменных выбрать ее параметры так, чтобы получаемая кривая наилучшим образом отражала экспериментальные данные. При этом делаются опреде­ленные предпосылки относительно случайной составляющей ε.

Предпосылки МНК:

1. случайный характер остатков

2. Нулевая средняя величина остатков не зависит от х_i

3. гомоскедастичность – дисперсия каждого отклонения ε_i одинакова при всех значениях х_i

4. отсутствие автокорреляции остатков. Значе­ния остатков ε_i распределены независимо друг от друга.

5. остатки подчиняются нормальному распре­делению.

6. модель должна быть линейной относительно параметров.

Рассмотрим задачу наилучшей аппроксимации набора наблюдений (x_t,y_t), t=1,2,..,n линейной функции f(x)=a+bx в смысле минимизации функционала:

Запишем необходимые условия экстремума: (находим частные производные функционала по параметрам и приравниваем к 0)

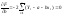
Раскроем скобки и получим стандартную форму нормальных уравнений:

(*)

Решение системы (*):

Замечание: из первого уравнения системы (*) следует что - уравнение прямой линии полученное в результатеmin-ции функ­ционала (*) проходит через (.) (х-,у-)

( х-,у-)-выборочные средние значения пере­менных X_t, Y_t

Замечание: мы предполагаем здесь что среди X_t не все числа одинаковые