
- •Введем в рассмотрение функции
- •Сделаем подстановку
- •Возвращаясь к старой переменной, получим
- •Вычисляя интегралы, сможем написать
- •Задача Коши для уравнения (2.2) ставится так: найти решение
- •Учитывая, что
- •Продолжая так и далее, будем получать последовательно
- •Искомое частное решение имеет вид
- •Итак, пусть дано неоднородное линейное уравнение
А.А.ПОТАПЕНКО
МАТЕМАТИКА, ч.1
Раздел
ОБЫКНОВЕННЫЕ
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
Санкт-Петербург Издательство СЗТУ
2007
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
СЕВЕРО-ЗАПАДНЫЙ ГОСУДАРСТВЕННЫЙ ЗАОЧНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
А.А.ПОТАПЕНКО
МАТЕМАТИКА, ч.1
Раздел
ОБЫКНОВЕННЫЕ
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
Утверждено редакционно-издательским советом университета в качестве учебного пособия
Санкт-Петербург Издательство СЗТУ
2007
Утверждено редакционно-издательским советом университета
УДК 517 (07)
Потапенко, А. А. МАТЕМАТИКА, ч.1, раздел: Обыкновенные дифференциальные уравнения: учебное пособие/А.А.Потапенко. СПб.:
Изд-во СЗТУ, 2007. - 70 с.
Учебное пособие соответствует требованиям государственных образовательных стандартов высшего профессионального образования по направлениям подготовки (специальностям) высшего профессионального образования:
080000 – Экономика и управление
140000 – Энергетика, энергетическое машиностроение и электротехника
150000 – Металлургия, машиностроение и материалообработка
190000 – Транспортные средства
200000 – Приборостроение и оптотехника
210000 – Электронная техника, радиотехника и связь
220000 – Автоматика и управление 230101 – Вычислительные машины, комплексы, системы и сети 240000 – Химическая и биотехнологии
261001 – Технология художественной обработки материалов
280202 – Инженерная защита окружающей среды
Учебное пособие предназначено для студентов 2 курса.
Рецензенты: кафедра вычислительной математики СЗТУ (зав.кафедрой Г.Г.Ткаченко, канд. физ.-мат. наук, доц.); В.М.Фролов, канд. физ.-мат. наук, доц. кафедры высшей математики Санкт-Петербургского государственного института точной механики и оптики (технического университета).
©Северо-Западный Государственный заочный технический университет, 2007
©Потапенко А.А.,2007
Предисловие
Эта книга является методическим пособием по разделу «Обыкновенные дифференциальные уравнения» для студентов СЗТУ второго курса. Пособие состоит из трех глав. Каждая глава разбита на части, в каждой из которых прилагается соответствующий вопрос программы. После введения необходимых определений и изложения соответствующего теоретического материала приводятся примеры, на которых демонстрируются применения изложенной теории.
В конце пособия помещен глоссарий – толковый словарь употребляемых терминов.
Введение
При решении многих задач естествознания и техники требуется найти функцию, которая удовлетворяет данному уравнению, содержащему эту неизвестную функцию, ее производные и независимые переменные.
Такие уравнения, в которых содержатся производные неизвестных функций, называются дифференциальными уравнениями.
Дифференциальные уравнения имеют большое прикладное значение, являясь мощным орудием исследования многих задач механики, астрономии, физики, радиотехники, теории автоматического управления и др. Это объясняется тем, что многие объективные законы записываются в форме дифференциального уравнения, связывающих неизвестную функцию, ее производные и независимые переменные. В этом случае сами эти уравнения являются средствами для количественного описания рассматриваемых законов. Например, законы механики Ньютона позволяют свести задачу исследования движения точки или твердого тела к изучению соответствующих дифференциальных уравнений. Расчет радиотехнических схем, вычисления траектории спутников, исследование устойчивости самолетов в полете, течение химических реакций - все это производится с помощью изучения дифференциальных уравнений. Роль дифференциальных уравнений особенно возросла в связи с развитием вычислительной техники.
3
Глава 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
1.1. Основные понятия
Неизвестные функции входящие в уравнения могут зависеть от одного или нескольких независимых переменных: в первом случае они называются обыкновенными дифференциальными уравнениями, во втором случае - дифференциальными уравнениями в частных производных.
Примером дифференциального уравнения в частных производных может служить уравнение
x |
∂2 z |
− y |
∂z |
= 2z, |
(1.1) |
|
∂y2 |
∂x |
|||||
|
|
|
z = z(x, y). В |
|||
служащее для определения функции |
двух |
переменных |
||||
дальнейшем мы будем рассматривать только обыкновенные дифференциальные уравнения.
Порядок старшей производной, входящей в дифференциальное уравнение, называется порядком этого уравнения.
Так, например, уравнения
y '+ xy2 = sin x, xy '3 +ex = 5, ln( y '2 + x2 ) − xtgy = ayx
являются уравнениями первого порядка, а уравнения xy ''− y '3 + 2xy = 0, y ''+5y '+6 y = 2x,
а также уравнение (1.1) - уравнениями второго порядка.
Очевидно, что любое обыкновенное дифференциальное уравнение n - го порядка с одной неизвестной функцией y аргумента x всегда можно
записать в виде |
|
|
|
F(x, y, y '',..., y(n) ) = 0, |
(1.2) |
||
где F - известная функция своих аргументов, |
причем производная |
y(n) |
|
обязательно содержится в уравнении. |
|
|
|
Решением дифференциального уравнения |
(1.2) на |
промежутке |
X |
называется функция y =ϕ(x) , которая n раз дифференцируемая на этом промежутке и при подстановке ее вместо y в уравнение (1.2) обращает
его в тождество на всем промежутке X , т.е.
F(x,ϕ(x),ϕ'(x),ϕ''(x),...,ϕ(n) (x)) ≡ 0, x X .
Например, функция y = x2 является решением уравнения xy '− 2 y = 0 на
всей оси.
График решения y =ϕ(x) дифференциального уравнения (1.2)
называется интегральной кривой этого уравнения.
Заметим, что иногда решение получают в неявной форме
4
Φ(x, y) = 0
или в параметрическом виде
x = x(t), y = y(t),
где t - параметр.
Процесс отыскания решений дифференциального уравнения называется интегрированием этого уравнения.
Одной из задач теории дифференциальных уравнений является интегрирование уравнений в квадратурах (в конечном виде), т.е. в получении замкнутой формулы, дающей (в явной, неявной или параметрической форме) выражение зависимости того или иного решения от аргумента, через заданные функции и интегралы от них. Квадратурой называется операция взятия неопределенного интеграла.
Отметим специально, что в теории дифференциальных уравнений под символом ∫ f (x)dx понимают какую-нибудь одну первообразную, а
постоянную интегрирования пишут отдельно.
В первую очередь мы займемся изучением дифференциального уравнения первого порядка, т.е. уравнением вида
F(x, y, y ') = 0,
где x - независимая переменная, y - его неизвестная функция, a F
заданная функция трех переменных в некоторой области пространства трех переменных. Если это уравнение может быть разрешено относительно производной y ', то получим уравнение вида
y ' = f (x, y), |
(1.3) |
где f (x, y) - известная функция, определенная в некоторой области D на плоскости Oxy . Уравнение вида (1.3) называют уравнением,
разрешенным относительно производной или уравнением в нормальной форме.
Уравнение (1.3) всегда можно записать в виде f (x, y)dx −dy = 0,
которое является частным случаем уравнения вида
P(x, y)dx −Q(x, y)dy = 0.
Последнее уравнение примечательно тем, что x и y равноправны, т.к.
из самого уравнения не следует, какая из переменных является независимой, а какая - функцией.
Геометрическая интерпретация уравнения (1.3). Пусть y = y(x)
означает некоторое решение уравнения (1.3), а M (x0 , y0 ) -произвольную
точку на графике этого решения. Проведем касательную к этому решению в точке M и обозначим через α угол, который образует эта
5
касательная с осью Ox . Тогда
tgα = y '(x0 ).
Но в силу уравнения (1.3)
y '(x0 ) = f (x0 , y0 ),
поэтому
tgα = f (x0 , y0 ).
Таким образом угол α наклона касательной к интегральной кривой в любой ее точке определен самим дифференциальным уравнением. Указывая это направление единичным вектором с серединой в точке M , мы получим в области D так называемое поле направлений. Интегральные кривые уравнения (1.3) суть кривые, для которых упомянутые направления являются направлениями касательных. Решить дифференциальное уравнение (1.3) означает найти все кривые, которые в каждой своей точке имеют направление, совпадающее с направлением поля.
Для построения поля направлений удобно рассматривать геометрические места точек, в которых касательные к интегральным кривым сохраняют постоянное направление. Кривая, в каждой точке которой направление поля, определяемое уравнением (1.3), одно и то же, называется изоклиной этого уравнения. Уравнения изоклин уравнения (1.3) имеют вид
f (x, y) = k,
где k = tgα = const.
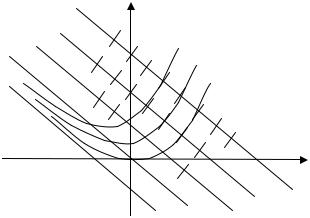
Пример 1.1. Правая часть уравнения y ' = x + y определена всюду на плоскости Oxy, следовательно, поле направлений для данного уравнения
можно построить во всей плоскости. Для того, чтобы упорядочить расстановку направлений поля, будем приравнивать последовательно правую часть данного уравнения числам -3,-2,-1,0,1,2,3 и т.д.
x+y=0 |
x+y=2 |
y |
|
|
Получим |
уравнения |
изоклин, |
|
|
|
которые в данном случае являются |
||||||
|
|
|
|
|||||
|
|
3 |
|
|
прямыми (рис. 1.1).На каждой из |
|||
|
|
|
|
|
этих изоклин штрихами |
показано |
||
|
|
2 |
|
|
направление поля. С помощью этих |
|||
|
|
1 |
|
|
направлений на рис. 1.1 изображено |
|||
|
|
|
x |
несколько |
интегральных |
кривых |
||
|
|
|
|
|||||
|
0 |
1 |
2 |
3 |
данного уравнения. |
|
|
|
|
Задача |
Коши. |
При |
решении |
||||
|
|
x+y=-1 |
x+y=1 |
x+y=3 |
||||
|
|
многих задач требуется найти не все |
||||||
|
|
|
|
|
||||
|
|
|
|
|
решения уравнения |
(1.3), |
а только |
|
|
Рис.1.1 |
|
|
6 |
|
|
|
|

такое, которое принимает заданное значение при заданном значении независимой переменной, а именно, требуется найти решение y(x),
удовлетворяющее условию |
(1.4) |
y(x0 ) = y0 , |
|
где x0 и y0 любые числа, для которых определена функция |
f (x, y). |
Условие (1.4) называют начальным условием, числа x0 и y0 - начальными
значениями решения уравнения (1.3), а саму задачу - задачей Коши или начальной задачей. С геометрической точки зрения задача Коши состоит в нахождении интегральной кривой, проходящей через данную точку
M (x0 , y0 ).
Прежде чем решать задачу Коши, надо быть уверенным, что искомое решение существует и единственное. На вопрос о существовании и единственности решения задачи Коши отвечает следующая теорема, которую мы приводим без доказательства и в упрощенной формулировке.
Теорема 1.1. Если в уравнении
|
y ' = f (x, y) |
∂f |
(1.3) |
функция |
f (x, y) и ее частная производная |
непрерывны в некоторой |
|
|
|
∂y |
|
области D на плоскости Oxy , то какова бы ни была точка (x0 , y0 ) области D , существует единственное решение y =ϕ(x) уравнения (1.3), определенное в некотором интервале, содержащем точку x0 и удовлетворяющее условию ϕ(x0 ) = y0 .
В частности, если два решения ϕ1 (x) и ϕ2 (x) уравнения (1.3)
совпадают хотя бы для одного значения x , то эти решения тождественно равны для всех тех значений x , для которых они оба определены.
Геометрический смысл этой теоремы состоит в том, что через каждую точку (x0 , y0 ) области D проходит одна и только одна интегральная
кривая уравнения (1.3) или, другими словами, вся область D покрыта интегральными кривыми уравнения (1.3), которые нигде не пересекаются между собой.
y |
|
|
|
|
Общее, |
частное и особое |
решения. |
|
|
yn |
|
Если закрепить начальное |
значение |
||||
|
|
|
абсциссы |
x0 , а начальному значению y |
||||
|
|
y3 |
|
|||||
|
|
|
придавать |
различные |
допустимые |
|||
|
|
y2 |
|
|
||||
|
|
y1 |
|
|
значения |
y1, y2 , y3 ,..., yn , |
то |
каждому |
0 |
|
|
|
x |
такому значению будет соответствовать |
|||
|
x0 |
|
||||||
|
|
|
||||||
|
|
|
|
единственная интегральная кривая (рис. |
||||
|
|
|
|
|
||||
|
Рис.1.2 |
7 |
|
|
|
|||
|
|
|
|
|
|
|
||
1.2) и, следовательно, в области D множество всех интегральных кривых образует семейство кривых, зависящих от одного параметра, который может изменяться в определенных пределах и который принято обозначать через C , так что все семейство интегральных кривых может быть описано уравнением
y =ϕ(x,C).
Определение. Функция |
|
y =ϕ(x,C). |
(1.5) |
непрерывно дифференцируемая по x называется общим решением уравнения (1.3) в области D , если она удовлетворяет следующим двум условиям:
1) равенство (1.5) разрешимо в области D относительно произвольной
постоянной C |
|
C = Ψ(x, y), |
(1.6) |
2) функция ϕ(x,C) является решением уравнения (1.3) |
для всякого |
значения постоянной C , полученной из формулы (1.6), в которой точка (x, y) - любая точка из области D .
Естественно, что знание общего решения (1.5) дает возможность решить задачу Коши для любых начальных значений x0 , y0 из области D .
Для этого достаточно заменить в формуле (1.5) переменные x и y числами x0 и y0 , решить полученное уравнение y0 =ϕ(x0 ,C) относительно C , т.е. получить соотношение
C= Ψ(x0 , y0 )
иподставить найденное значение в общее решение (1.5). Полученная
функция
y =ϕ(x, Ψ(x0 , y0 ))
и есть искомое решение.
Общее решение уравнения (1.3), записанное в виде, не разрешенном относительно искомой функции, т.е. в виде
Φ(x, y,C) = 0 èëè Φ(x, y) = C
называют общим интегралом этого уравнения.
Решение, которое получается из общего решения y =ϕ(x,C), если в
последнем произвольной постоянной C придать конкретное (допустимое) значение, называется частным решением.
Аналогично определяются частные интегралы.
Решение, которое не может быть получено из общего решения (общего интеграла) ни при каком конкретном значении произвольной постоянной, называется особым решением. Геометрически особому решению соответствует интегральная кривая, не содержащаяся в семействе
8

интегральных кривых, составляющих общее решение (общий интеграл). Особое решение примечательно тем, что через каждую точку изображающей его интегральной кривой проходит, по крайней мере, еще одна интегральная кривая того же уравнения, имеющая в этой точке ту же касательную.
Если правая часть уравнения (1.3) удовлетворяет в области D условиям теоремы 1.1, то это уравнение не имеет в области D особых решений.
Пример 1.2. Рассмотрим уравнение
|
|
|
|
|
|
|
|
|
|
|
y ' = 33 y2 . |
(1.7) |
Так |
как правая |
часть |
уравнения (1.7) и ее частная |
производная |
||||||||
|
∂ |
(33 y2 ) = 3 |
2 |
y− |
1 |
= |
|
2 |
|
|
||
|
3 |
|
удовлетворяют условиям теоремы 1.1 во всех |
|||||||||
|
∂y |
3 |
|
y |
||||||||
|
|
|
|
|
|
3 |
|
|
||||
точках плоскости Oxy за исключением точек оси Ox , то через любую точку (x0 , y0 ) при y0 ≠ 0 проходит единственная интегральная кривая
уравнения (1.7). Для отыскания общего решения запишем уравнение (1.7) в виде
1 |
|
|
− |
2 |
|
|
y |
3 dy = dx. |
|||
|
|
|
|||
3 |
|
||||
|
|
|
|
||
1
В левой части равенства стоит дифференциал функции y3 , а в правой -
дифференциал функции x . Из равенства дифференциалов этих функций следует, что сами эти функции могут отличаться лишь на произвольное постоянное слагаемое C , так что можем написать
1
y3 = x +C
или в таком виде |
|
y = (x +C)3. |
(1.8) |
Функция (1.8) является |
общим |
yрешением уравнения (1.7) всюду на плоскости Oxy за исключением оси Ox .
|
|
|
|
|
|
Непосредственно видно, что подставив |
||||||
|
|
0 |
|
|
x |
|||||||
|
|
|
|
функцию y = 0 в уравнение (1.7) получим |
||||||||
-3 |
|
|
5 |
|
||||||||
|
1 |
3 |
|
тождество, |
т.е. |
y = 0 |
является |
решением |
||||
|
|
|
|
|
|
|
|
|
|
|
||
3 |
y=x |
3 |
|
3 |
|
данного |
уравнения, |
притом |
особым |
|||
y=(x+2) |
y=(x-2) |
|
y=(x-4) |
решением, |
т.к. |
оно |
не |
может быть |
||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получено из общего решения y = (x +C) |
3 |
|||||
|
|
|
|
|
|
|
||||||
Рис.1.3 |
|
|
|
ни при каком |
значении |
постоянной C . |
||||||
|
|
|
9 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что через каждую точку |
|
M0 (x0 , 0) оси Ox проходит кривая |
|||||
y = (x − x )3 , совпадающая при |
y |
0 |
≠ 0 |
с общим |
решением (1.8) и |
||
|
0 |
|
|
|
|
|
|
касательной к которой в этой точке является сама ось Ox (рис. 1.3). |
|||||||
В |
дальнейшем |
слова |
решить |
(или |
проинтегрировать) |
||
дифференциальное уравнение будут означать одно из двух:
а) найти его общее решение (общий интеграл), если начальные условия не заданы;
б)найти частное решение (частный интеграл), удовлетворяющее заданным начальным условиям.
Ниже будут рассмотрены некоторые типы дифференциальных уравнений первого порядка, интегрируемых в квадратурах, и указаны пути получения общего решения (общего интеграла).
1.2. Уравнения с разделяющимися переменными
Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если его можно записать в виде
y ' = f (x) g( y), |
(1.9) |
где функция f (x) определена и непрерывна на интервале |
(a,b), а |
функция g( y) определена и имеет непрерывную производную на интервале (c, d). Предположим, что функция g( y) не обращается в нуль на интервале (c, d).
Уравнения такого вида, т.е. уравнения, правая часть которых (после разрешения относительно производной y ') представляется в виде
произведения функции, зависящей только от аргумента x , на функцию, зависящую только от искомой функции y , называют уравнениями с
разделяющимися переменными, ибо умножив обе части уравнения (1.8) на dx и разделив на g( y) , получим
dy |
= f (x)dx, |
(1.10) |
|
g( y) |
|||
|
|
где в левой части находится функция от y и dy , а в правой - функция от x и dx .
Введем в рассмотрение функции |
dy |
|
|
|
G( y) = ∫ |
, F(x) = ∫ f (x)dx. |
(1.11) |
||
g( y) |
||||
|
|
|
Понимая под y решение уравнения (1.9), заметим, что в левой части равенства (1.10) стоит дифференциал функции G( y), а в правой - дифференциал функции F(x). Из равенства этих дифференциалов
10

следует, что сами функции G( y) и F(x) могут отличаться друг от друга
лишь на произвольное постоянное слагаемое C , так что можем написать
G( y) = F(x) +C
или, используя обозначение (1.11), |
|
|||
∫ |
dy |
= ∫ f (x)dx +C. |
(1.12) |
|
g( y) |
||||
|
|
|
||
Последнее соотношение представляет собой общий интеграл
уравнения (1.9) в прямоугольнике |
|
{a < x < b, c < y < d}. |
(1.13) |
Рассмотрим теперь случай, когда функция g( y) обращается в нуль при
некотором y0 (c, d ), так что g( y0 ) = 0. Подставив в |
уравнение (1.9) |
y = y0 , легко заметить, что оно удовлетворяется, т.е. |
y = y0 является |
решением уравнения (1.9). При этом решение y = y0 |
не содержится в |
соотношении (1.12) и, следовательно, соотношение (1.12) в этом случае уже не будет общим интегралом уравнения (1.9) в прямоугольнике (1.13).
Заметим, что уравнение с разделяющимися переменными иногда может быть задано в симметричной относительно x и y форме:
|
|
f1 (x)g1 ( y)dx + f2 (x)g2 ( y)dy = 0, |
|
(1.14) |
||
где |
функции |
f1 (x), f2 (x), g1 ( y), g2 ( y) |
заданы |
и |
непрерывны |
|
соответственно в интервалах (a,b) и (c, d), , причем |
g1 ( y) и f2 (x) |
не |
||||
обращаются в нуль. |
|
|
|
|
|
|
Разделив обе части уравнения (1.14) на произведение |
g1 ( y) f2 (x) |
и |
||||
проведя аналогичное рассуждение, получим общий интеграл уравнения (1.14) в прямоугольнике (1.13) в следующем виде
∫ f1(x) dx + ∫ g2 ( y) dy = C, f2 (x) g1( y)
где C - произвольная постоянная. Пример 1.3. Найти решение уравнения
y ' = x4 (1+ y2 ),
удовлетворяющее начальному условию y(0) =1.
Данное уравнение есть уравнение с разделяющимися переменными,
записанное в виде (1.9) (здесь f (x) = x4 , |
а g( y) =1+ y2 ). Функции x4 и |
|||
(1+ y2 ) 'y = 2 y непрерывны при любых |
значениях |
x |
и y , причем |
|
1 |
+ y2 ≠ 0. Умножая обе части данного уравнения на |
dx |
и разделив на |
|
1 |
+ y2 , будем иметь |
|
|
|
11
dy |
= x4dx. |
|
1+ y2 |
||
|
Выполняя операции интегрирования, получим общий интеграл данного уравнения на всей плоскости Oxy в виде
arctgy = |
x5 |
+C, |
(1.15) |
|
5 |
||||
|
|
|
где C - произвольная постоянная.
Для решения поставленной задачи Коши положим в полученном общем интеграле x = 0, y =1. Будем иметь
arctg1 = C
т.е. C = π4 . Подставив найденное значение C в равенство (1.15) и
разрешив относительно y , получим частное решение, удовлетворяющее заданному начальному условию
|
x |
5 |
|
π |
|
|
y = tg |
|
+ |
. |
|||
5 |
4 |
|||||
|
|
|
||||
Пример 1.4. Решить уравнение
x(1− y2 )dx + y(1− x2 )dy = 0.
|
|
Данное |
дифференциальное |
|
уравнение |
есть |
уравнение |
с |
|||||||
разделяющимися переменными, записанное в виде (1.14) (здесь |
f1 (x) = x, |
||||||||||||||
f |
2 |
(x) =1− x2 |
, |
g ( y) =1− y2 , |
g |
2 |
( y) = y). |
|
Функции |
x, |
1− x2 , |
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
(1− y2 )'y = −2 y, |
( y) 'y =1 непрерывны при |
любых значениях |
x и |
y , |
|||||||||||
причем будем пока считать, что 1− x2 ≠ 0 и 1− y2 ≠ 0. |
|
|
|
||||||||||||
|
|
Разделив обе части данного уравнения на произведение (1− y2 )(1− x2 ), |
|||||||||||||
получим |
|
|
x |
|
|
|
y |
|
|
|
|
|
|
||
|
|
|
|
|
dx + |
|
dy = 0. |
|
(1.16) |
||||||
|
|
|
|
1− x2 |
1− y2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Умножая уравнение (1.16) на число (−2) |
и замечая, что при этом в |
||||||||||||
числителе каждой дроби стоит производная знаменателя, сможем написать в результате интегрирования
ln |1− x2 | +ln |1− y2 |= ln C,
где произвольная постоянная обозначена через ln C , что возможно, если принять C > 0. Последнее равенство можно записать в виде
|1− x2 | |1− y2 |= C.
Мы получили общий интеграл данного уравнения, при условиях 1− x2 ≠ 0
12

и 1− y2 ≠ 0.
Рассмотрим теперь случай 1− y2 = 0, т.е. y = ±1. Непосредственно из данного уравнения видно, что каждый из случаев y =1 и y = −1 является
решением. При этом они содержатся в общем интеграле и могут быть получены из него при C = 0.
Аналогично рассматриваются решения, доставляемые уравнением
1− x2 = 0, т.е. x =1 и x = −1.
Пример 1.5. Решить уравнение
xyy '+ x2 −1 = 0
при x >1.
Для установления типа данного уравнения умножим обе его части на dx . Получим уравнение
xydy +(x2 −1)dx = 0,
которое имеет вид уравнения (1.14) и, следовательно, является уравнением с разделяющимися переменными.
Для разделения переменных разделим обе части последнего уравнения
на x . Будем иметь |
1 |
|
|
|
|
||
ydy + x − |
|
dx = 0. |
|
x |
|||
|
|
Выполняя операции интегрирования, сможем написать
y2 + x2 −ln x = C, 2 2
где C - произвольная постоянная. Разрешая относительно y2 , получим окончательно
y2 = 2 ln x − x2 +C,
где произведение 2C вновь обозначено через C .
1.3. Однородные уравнения
Рассмотрим еще один тип дифференциальных уравнений первого порядка, интегрируемых в квадратурах. Прежде чем дать определение этого типа уравнений, приведем понятие об однородной функции.
Определение. Функция Φ(x, y) называется однородной функцией степени m относительно переменных x и y , если умножение каждого из
ее аргументов на одно и то же произвольное число λ > 0 |
равносильно |
умножению ее на λm , а именно |
|
Φ(λx, λy) = λm Φ(x, y), |
(1.17) |
где m - действительное число. |
|
13
