Лекция 2. Элементы теории матричных игр

1. Платежная матрица. Нижняя и верхняя цена игры

Теория игр - это математическая теория конфликтных ситуаций. Математическая модель конфликтной ситуации называется игрой. Конфликтная ситуация возникает тогда, когда ее участники (игроки) имеют противоположные интересы.

Задачей теории игр является выработка рекомендаций для игроков, т.е. определение для них оптимальной стратегии. Стратегией игрока называется система правил, однозначно определяющих поведение игрока на каждом ходе в зависимости от ситуации, сложившейся в процессе игры. Оптимальной называется стратегия, которая при многократном повторении игры обеспечивает данному игроку максимально возможный средний выигрыш.

Рассмотрим простейшую математическую модель конечной конфликтной ситуации, когда имеются два участника и когда выигрыш одного равен проигрышу другого (антагонистическая игра двух лиц с нулевой суммой).

Задача первого игрока – максимизировать свой выигрыш. Задача второго игрока – минимизировать свой проигрыш.

Игру можно представить в виде матрицы, в которой строки – стратегии первого игрока, столбцы – стратегии второго игрока, а элементы матрицы – выигрыши первого игрока. Такую матрицу называют платежной.

В общем случае парную игру с нулевой суммой можно записать платежной матрицей

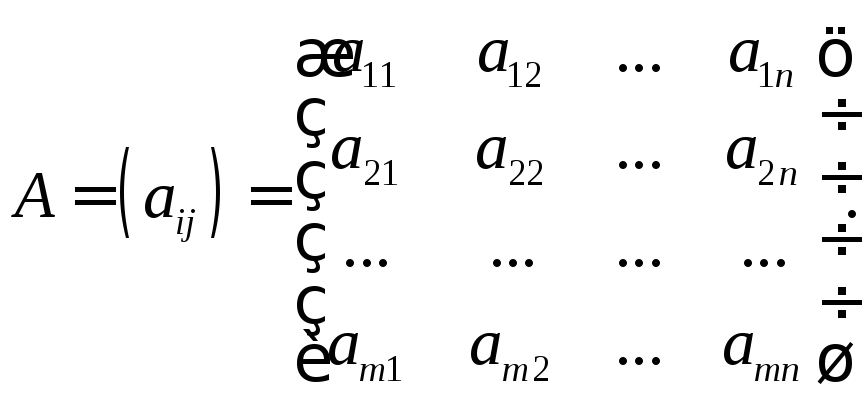
Найдем наилучшую стратегию первого игрока: минимальное число в каждой строке обозначим,

.

Зная, первый игрок выберет ту стратегию, для котороймаксимально. Обозначим это максимальное значение, тогда

.

Величина - гарантированный выигрыш, который может обеспечить себе первый игрок, - называется нижней ценой игры.

Аналогично для определения наилучшей стратегии второго игрока находят максимальные значения выигрыша по столбцам и, выбрав из них минимальное значение, получаем

,

где – верхняя цена игры.

Для матричной игры справедливо неравенство .

Если , то такая игра называется игрой с седловой точкой, а пара оптимальных стратегий – седловой точкой матрицы. В этом случае элемент, называемый ценой игры, является минимальным в-й строке и максимальным вj-м столбце.

Рассмотренные оптимальные стратегии первого и второго игроков называются соответственно максиминными и минимаксными.

Пример 1. Решить игру, заданную матрицей

А=.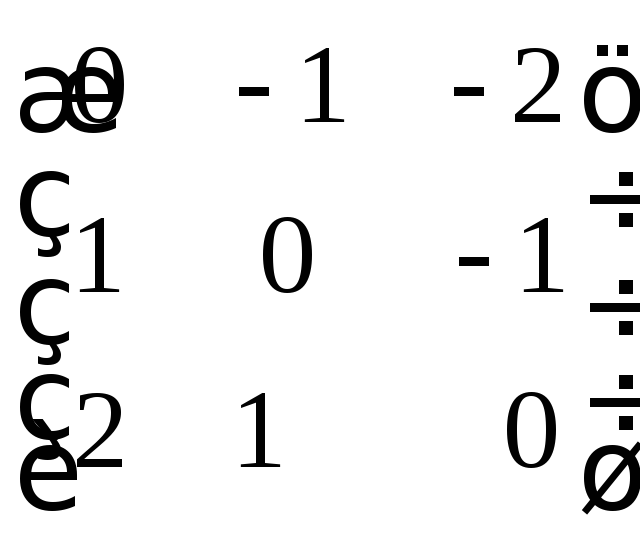

Решение. Находим нижнюю и верхнюю цены игры

Так как матрица Н имеет седловую точку , то цена игры равна 0, при этом первый игрок должен выбрать третью строку, а второй игрок должен выбрать третий столбец. Отклонение от указанной стратегии приводит к уменьшению выигрыша первого игрока или к увеличению проигрыша второго игрока.

2 Приведение матричной игры к задаче линейного программирования.

Теория игр находится в тесной связи с линейным программированием, т.к. каждая игра двух лиц с нулевой суммой может быть представлена как задача линейного программирования и решена симплексным методом.

Рассмотрим стратегии игроков, основанные на вероятностном выборе ходов. Такие стратегии называются смешанными. Пусть я строка выбирается первым игроком с вероятностью (= 1,2,...,m), a j-й столбец выбирается вторым игроком с вероятностью (j = l,2,...,n). Так как одна из строк и один из столбцов будут обязательно выбраны (каждый игрок обязан сделать ход), то

Цена игры V определяется как математическое ожидание величины а, т. е.

V=

Для первого игрока математическая модель задачи записывается в виде

при ограничениях:

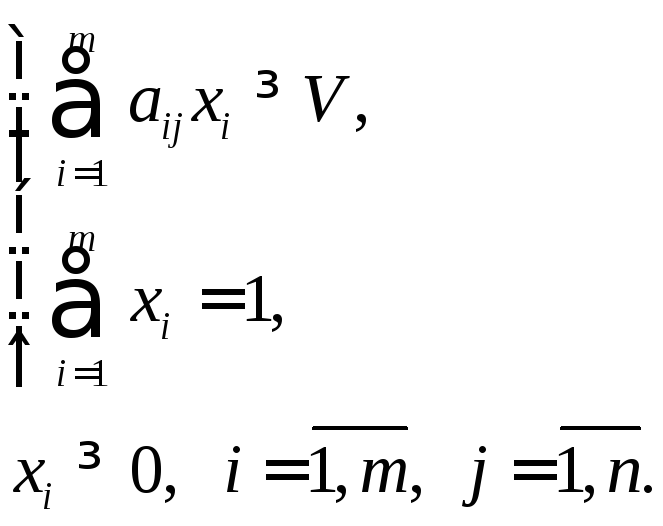
Математическую модель можно упростить, разделив все (+1) ограничений на цену игры. Полагая, что>0, систему ограничений можно записать так:

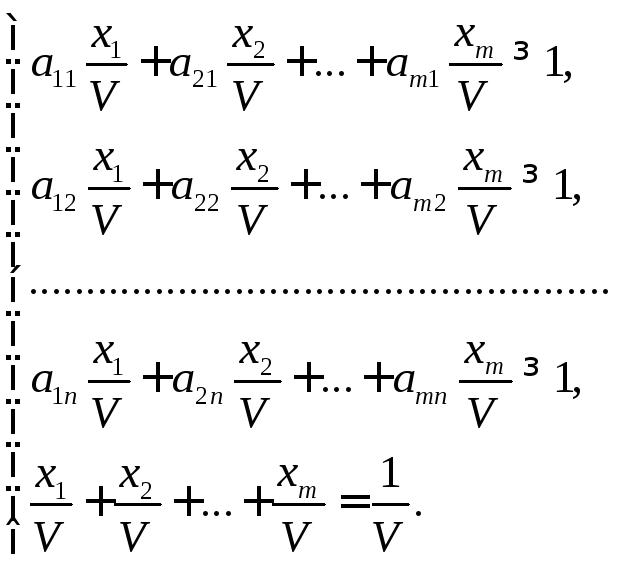
Пусть . Так как→max, то. Получим задачу линейного программирования вида

при ограничениях:

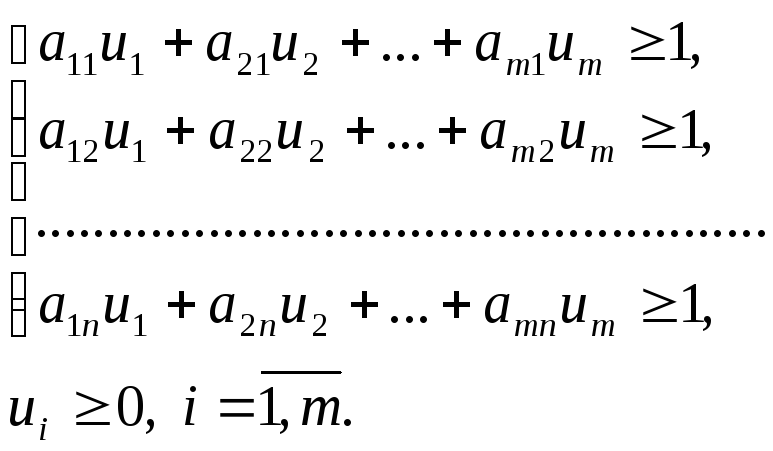
Задача второго игрока является двойственной по отношению к задаче первого игрока и имеет вид.

при ограничениях:

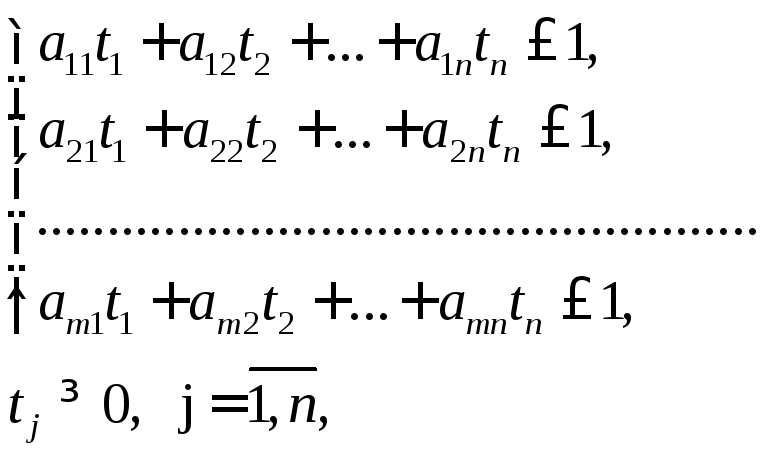
где

Можно найти решение одного из игроков, а затем по теоремам двойственности – решение другого.

Пример 2. Решить игру, заданную матрицей

.

Решение Находим нижнюю и верхнюю цену игры.

= max(l;3) = 3;

Так как они не равны, то применяем смешанные стратегии. Находим сначала оптимальную стратегию второго игрока, т.е. находим наибольшее значение функции и соответствующие значения неотрицательных переменных ,, если выполняются неравенства:

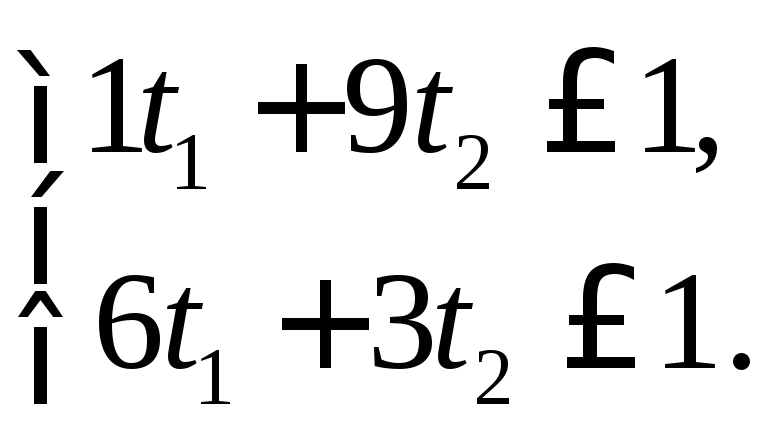
Для решения этой задачи используем симплексный метод, проводя вычисления в таблицах.

		Таблица 1					Таблица 2
	1	9	1			1/9	1/9	1/9
	6	3	1			51/9	-3/9	6/9
	-1	-1	0			-8/9	1/9	1/9

Таблица 3

	1/51	6/51	5/51
	9/51	-3/51	6/51
	8/51	3/51	11/51

Таким образом, имеем: = 6/51,t₂ = 5/51, = 51/11,y= 6/51 • 51/11 = 6/11, у₂ = 5/51 • 51/11 = 5/11. Итак, второй игрок должен выбирать первый столбец с вероятность 6/11, а второй 5/11.Используем соответствие t₃u, t ₄u, то из таблицы 3 имеем:u= 3/51, u₂ = 8/51.Следовательно, x= 3/51 • 51/11 = 3/11, х₂ = 8/51 • 51/11 = 8/11. . Итак, первый игрок должен выбирать первую строку с вероятность 3/11, а вторую 8/11 .