Лекция 1 Задачи линейного программирования

1. Задача оптимального планирования производства

Пусть предприятие из видов ресурсов производитвидов продукции. При этом для производства одной единицыj-го вида продукции расходуетсяединицi-го вида ресурса, т.е.норма расходаi-го ресурса на производствоj-го вида продукции. Матрица, составленная из норм расхода, называется матрицей норм расхода или технологической матрицей.

Обозначим через величину прибыли от реализации одной единицыj-го вида продукции. Эти значения прибыли запишем матрицей-строкой. План производства продукциих₁,х₂, …,х_побозначим матрицей-столбцомХ. Тогда произведение матрицпредставляет собой величину прибыли, полученной после реализации продукции.

Количество i-го ресурса обозначим. Значенияb₁,b₂, …,b_m запишем матрицей-столбцомB. Тогда матричное неравенствоозначает необходимость, учитывать ограниченность ресурсов при рассмотрении планов производстваХ. Если это неравенство выполняется, то планявляется реальным или допустимым. Естественно, нужно найти такой допустимый план, который бы обеспечил наибольшую прибыль.

Эту задачу можно записать так:

.

Или в матричной форме:

,

,.

Такая задача называется задачей оптимального планирования производства. Функция называется целевой функцией. Множество всех плановХ, удовлетворяющих неравенствам,, называется множеством допустимых планов, и обозначаетсяD. Тогда нашу задачу можно сформулировать так: найти максимум целевой функциина множестведопустимых планов.

Область ограничений задается линейными функциями. Сама целевая функция также является линейной. Задачи такого вида называются задачами линейного программирования. К ним относятся, например, задачи о диете, о раскрое материала и другие.

Задача линейного программирования в общем виде такова: найти максимум или минимум линейной целевой функции при линейных ограничениях на переменные.

2. Графический метод решения задач линейного программирования

Пусть задача линейного программирования содержит две переменные, и. Графический метод ее решения состоит в следующем.

В системе координат строим многоугольник, который определяется системой ограничений. Целевая линейная функцияпри фиксированном значенииявляется уравнением прямой, называемой опорной прямой.

Значение целевой функции возрастает при движении прямойв направлении нормального вектора этой прямой. Перемещая эту прямую параллельно себе в направлении векторапо построенному многоугольнику ограничений, определяем вершины входа и выхода (может быть отрезок или луч).

Вершина, из которой выходит опорная прямая, дает максимальное значение, в которую приходит минимальное значение целевой функции. Определяем координаты этих вершин, и находим соответствующие значения целевой функции, подставляя координаты в выражение для целевой функции.

Пример.Решить графическим методом задачу линейного программирования: найти максимальное значение функциипри ограничениях

,

;

,.

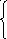Решение.В системе координатна плоскости строим прямуюпо двум точкам с координатамиив первой четверти, так как. Прямая делит плоскость на две полуплоскости, из которых нужно выбрать одну, удовлетворяющую первому неравенству в системе. Для этого возьмем точкуи подставим в неравенство. Если неравенство выполняется, то нужно заштриховать ту полуплоскость, в которой находится точка. Аналогично поступают с прямой. Получаем, что областью решений неравенств является четырехугольник.

Строим опорную прямую , и перемещаем ее параллельно себе в направлении векторапо четырехугольнику, определяем вершину выхода – точкуВ.

Находим координаты точки В, для этого решаем систему уравнений:

Найденные координаты точки подставляем в целевую функцию, и определяем максимальное значение:

.

Данное значение можно найти, если подставить координаты вершин четырехугольника в целевую функцию и выбрать среди них максимальное значение.