
Дубовик О.А., Совертков П.И
.pdf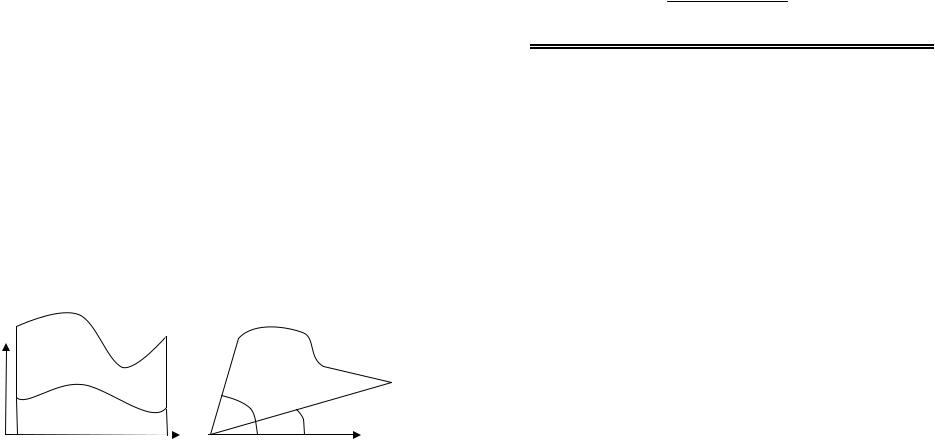
О.А. Дубовик П.И. Совертков
МАТЕМАТИЧЕСКИЙ АНАЛИЗ - II
(функции нескольких переменных, интегральное исчисление функции одной переменной)
Методическое пособие для студентов заочного отделения
у |
y = f2 (x) |
|
|
|
|
|
|
|
|
|
r = r (ϕ) |
||
|
|
|
|
|
||
|
y = f1 (x) |
β |
|
|
|
|
|
|
|
α |
ρ |
||
|
х |
|
|
|||
О a |
b |
О |
|
|
|
|
|
b |
|
1 |
β |
|
|
S = ∫( f2 (x) − f1 (x)) dx |
S = |
∫r2 (φ) dφ |
||||
2 |
||||||
|
a |
|
α |
|
||
Сургут
2009
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И НАУКИ ХАНТЫ-МАНСИЙСКОГО АВТОНОМНОГО ОКРУГА – ЮГРЫ
ГОУ ВПО «СУРГУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ХАНТЫ-МАНСИЙСКОГО АВТОНОМНОГО ОКРУГА – ЮГРЫ»
Кафедра высшей математики
О.А. Дубовик П.И. Совертков
МАТЕМАТИЧЕСКИЙ АНАЛИЗ-II
(функции нескольких переменных, интегральное исчисление функции одной переменной)
Методическое пособие для студентов заочного отделения
Сургут Издательский центр СурГУ
2009
1
УДК 517(072) + 517.3(072) ББК 22.161.1 я 73
Д796
Д796 Дубовик, О. А. Математический анализ-II (функции нескольких переменных, интегральное исчисление функции одной переменной) : метод. пособие для студентов заочного отделения / О. А. Дубовик, П. И. Совертков ; Сургут. гос. ун-т ХМАО – Югры. – Сургут : ИЦ СурГУ, 2009. – 68 с.
Впервой части пособия приведены варианты двух контрольных работ по темам: функция нескольких переменных и интегральное исчисление функции одной переменной, а также программа курса и вопросы к экзамену за второй семестр. Во второй части пособия рассматриваются методические указания по нахождению интегралов. Большое внимание уделено применению интегрального исчисления при решении задач. Пособие содержит весь необходимый справочный материал.
Предназначено для студентов заочного отделения факультета информационных технологий, а также может быть использовано для студентов дневного отделения как справочное пособие при выполнении самостоятельной работы.
Печатается по решению редакционно-издательского совета СурГУ.
Рецензент А.П. Кармазин, доктор физико-математических наук, профессор кафедры прикладной математики Сургутского государственного университета.
©Дубовик О.А., Совертков П.И., 2009
©ГОУ ВПО «Сургутский государственный университет ХМАО – Югры», 2009
2
Содержание |
|
I. Контрольная работа № 3............................................................. |
4 |
II. Контрольная работа № 4............................................................ |
6 |
III. Программа курса...................................................................... |
8 |
IV. Список рекомендуемой литературы........................................ |
10 |
V. Вопросы к экзамену................................................................ |
11 |
VI. Справочные материалы.......................................................... |
13 |
VII. Решение задач с функцией от нескольких переменных........... |
34 |
VIII. Применение производной функции нескольких переменных... |
38 |
IX. Методы нахождения неопределенного интеграла.................... |
44 |
X. Методывычисленияопределенных инесобственных интегралов.. |
53 |
XI. Основные направления применения интеграла........................ |
60 |
XII. Некоторые линии.................................................................. |
66 |
3
I.Контрольная работа № 3
№10–19. С помощью дифференциала приближенно вычислить.
10. |
1, 01 |
|
. |
11. |
0,97 |
. 12. |
4,08 |
. |
13. |
9, 01 |
|
|
|
. |
|||||||||||||
|
0,98 1, 02 |
|
1,02 0,99 |
1, 01 0,99 |
4, 02 1,01 |
||||||||||||||||||||||
14. |
1,012,03. |
|
|
15. |
2,011,02. |
16. |
|
1,02 1, 01 |
. |
17. |
|
0,99 1, 02 |
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0,98 |
|
|
|
0,97 |
|
|
|
|
|||||||
18. |
|
1,03 |
. |
19. |
|
|
0,99 0,98 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1, 01 0,98 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1, 02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
№ 20–29. Найти вторые дифференциалы d 2u функции. |
|
|
|
|
|||||||||||||||||||||
20. |
u = f (x2 + y2 , x2 − y2 ). |
21. u = f xy, |
x |
. 22. u = |
|
f |
1 |
, |
|
x |
. |
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
xy |
y |
|||||||||
23. |
u = f (x + y, y2 − x2 ). |
24. u = f ( y − x, x2 + y2 ). |
|
|
|
|
|
|
|
|
|
||||||||||||||||
25. |
u = f ( y + x2 , x − y2 ). |
26. u = f (x + y − z, x + y + z). |
|
|
|
|
|||||||||||||||||||||
27. |
u = x f (x y, x + y). |
|
|
28. u = xy f (x + y, x − y). |
|
|
|
|
|
|
|
|
|
||||||||||||||
29.u = f (x − 2 y + z, x − y − z).
№30–39. Найти производную функции z = f (x, y) в точке M по направлению к точке N.
30. |
z = x3 −3x2 y + 3xy2 − y3 , M (1,1), N (2, 2). |
|||||
31. |
z = 6x2 +12xy + y2 , |
M (0,1), N (0, 2). |
||||
32. |
z = arctg (xy), |
M (1,0), N (0,1). |
||||
33. |
z = arctg |
y |
, |
M (0,1), N(1,0). |
||
|
||||||
|
|
x |
|
|
|
|
34. |
z = ln (x2 |
+ 2 y2 ), |
M (1,1), N (0,0). |
|||
35. |
z = sin(x − 2 y), M (0,0), N (2,1). |
|||||
36. |
z = x3 +12x2 y + xy2 , |
M (1,1), N (0, 0). |
||||
37. |
z = x ln (x2 + y2 ), |
M (1,0), N (0, 2). |
||||
38. |
z = y ln (2x2 + y2 ), |
|
M (0, 2), N (0,1). |
|||
39. |
z = (x − y) ln (x2 + y2 ), M (1,0), N (2, 0). |
|||||
|
|
|
|
|
|
4 |
№ 40–49. Исследовать на условный экстремум функцию z = f (x, y) на линии γ.
40. |
z = x + 2 y, |
γ : x2 |
+ 4 y2 |
= 4. |
41. |
z = x −3y, |
γ : 4x2 + 9 y2 = 4. |
42. |
z = −x − y, |
γ : x2 |
+ y2 =1. |
43. |
z = x − y, |
γ : x2 + 4 y2 = 4. |
|
44. |
z = x − y, |
γ : 4x2 + y2 |
=1. |
45. |
z = −2x + y, |
γ : 4x2 + 4 y2 =1. |
|
46. |
z = x − 2 y, |
γ : x2 |
+ 4 y2 |
=1. |
47. |
z = x2 + y2 , |
γ : x2 + y =1. |
48. |
z = x2 + y2 , |
γ : 2x2 + y =1. |
49. |
z = 4x2 + y2 , |
γ : y = x2 +1. |
||
5
II.Контрольная работа № 4
№50–59. Найти неопределенный интеграл.
50. а) ∫xsin 2x dx; |
б) ∫ |
xdx |
|
; |
в) ∫ |
|
|
dx |
|
; |
г) ∫sin3 x cos2 xdx. |
x − |
1 |
1 |
+ x |
3 |
|||||||
|
|
|
|
|
|
|
|||||
51. а) |
∫x cos 2x dx; |
б) ∫ |
|
|
|
xdx |
; |
|
|
|
|
|||
|
x |
+1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
52. а) |
∫xe−3x dx; |
б) |
∫ |
|
|
|
|
dx |
|
|
; |
|
||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
x +1 |
|
|
|||||
53. а) |
∫x arcctgx dx; |
б) |
∫ |
|
|
|
dx |
|
|
; |
|
|||
1 |
|
|
|
|
||||||||||
|
|
|
|
|
− x |
|
|
|||||||
54. а) |
∫ln (1 + x2 ) dx; |
б) |
∫ |
|
|
|
dx |
; |
|
|
||||
1 |
x |
|
|
|||||||||||
|
|
|
|
|
+ e |
|
|
|
|
|
|
|||
55. а) |
∫ arcctg x dx; |
б) |
∫ |
|
|
|
dx |
|
|
|
|
|
; |
|
|
x |
x + |
1 |
|||||||||||
|
|
|
|
|
|
|
||||||||
в) |
∫ |
|
|
|
|
dx |
; |
|
|
|
||||
1 |
3 |
|
|
|||||||||||
|
|
|
− x |
|
|
|
|
|
|
|||||
в) |
∫ |
|
|
|
|
dx |
|
|
|
|
; |
|||
|
x |
4 |
|
|
2 |
|||||||||
|
|
|
|
|
− x |
|
|
|
|
|||||
в) |
∫ |
|
|
x3 +1 |
dx; |
|||||||||
x |
3 |
− x |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
в) |
∫ |
|
|
x3 −1 |
|
|
|
dx; |
||||||
|
x |
3 |
|
+ x |
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
в) ∫ dx ; x4 −1
г) ∫sin3 x cos2 xdx.
г) ∫ cos3 xdx.
г) ∫1 −sincosx x dx.
г) ∫1 +sincosx x dx. г) ∫1 −cossinx x dx.
56. а) |
∫x ln x dx; |
|
б) |
∫ |
|
|
|
dx |
|
; |
|
|
|
в) |
∫ |
x2 dx |
; |
|
|
г) |
∫sin x (1 −cos x) dx. |
|||||||||||||||||||||||||
|
|
1 + e |
x |
|
|
|
4 |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||
57. а) |
∫ln2 x dx; |
б) |
∫ |
|
|
; |
|
в) |
∫ |
|
|
|
|
|
|
|
dx; |
|
|
г) |
|
∫ |
sin |
x |
dx. |
|||||||||||||||||||||
|
|
|
− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
+ e |
|
|
|
|
|
|
|
|
|
(x |
|
+1)(x |
|
+ x) |
|
|
|
|
|
|
|
cos |
x |
|
|
||||||||||||
58. а) |
∫xsin x |
2 |
dx; |
|
|
б) |
|
∫ |
|
|
dx |
|
|
|
; |
|
|
в) |
∫ |
|
dx |
|
; |
|
г) |
∫ |
cos2 x |
dx. |
||||||||||||||||||
|
|
|
|
1 |
− e |
−x |
|
|
|
|
x(x |
2 |
+1) |
|
sin |
4 |
x |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
59. а) |
∫x cos x2 dx; |
б) |
∫ |
|
|
|
dx |
; |
|
в) |
|
∫ |
|
|
dx |
|
|
|
; |
г) |
∫ |
|
|
|
|
|
dx |
|
|
|
. |
|||||||||||||||
|
|
|
− x |
|
|
x(1 − x |
2 |
) |
|
sin |
2 |
x cos |
2 |
x |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 − e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
∫b |
|
|
№ 60–69. Вычислить приближенно по формуле Симпсона |
|||||||||||||||||||||||||||||||||||||||||||
f (x)dx, разбив [a; b] |
на 10 частей. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60. |
∫1 |
3 x2 +1 dx. |
61. |
|
∫1 |
3 1 − x2 |
dx. |
|
62. |
∫2 |
3 8 + x2 dx. |
63. |
|
∫2 |
|
3 8 − x2 dx. |
||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
64. |
12∫ |
4 + x2 dx. |
65. |
|
∫2 |
|
|
4 − x2 |
|
dx. |
|
66. ∫1 |
|
1 + x3 dx. |
67. |
∫1 |
|
1 − x3 dx.. |
||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
68. ∫2 |
8 − x3 dx. |
69. ∫1 |
|
|
4 + x3 dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ 70–79. Исследовать на сходимость несобственные интегралы.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
+∞ |
|
|
dx |
|
|
|
+∞ |
|
dx |
|
|
|
+∞ |
|
2xdx |
|
|
2 |
||||||
70. |
∫ |
|
|
|
. |
71. |
∫ |
|
|
. |
72. |
∫ |
|
. |
73. ∫ctg xdx. |
||||||||||
x |
2 |
+ 2x + |
2 |
|
|
x |
|
|
2 |
|
|||||||||||||||
|
−∞ |
|
|
|
1 |
|
|
|
|
|
−∞ x |
|
+1 |
|
0 |
||||||||||
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
dx |
|
|
+∞ arctg x |
|
|
||||||||
74. |
∫ tgx dx. |
|
|
75. ∫ |
|
|
|
|
|
|
. 76. |
∫ |
|
|
|
|
|
|
dx. |
|
|||||
|
|
|
3 (x −1) |
2 |
|
x |
2 |
+1 |
|
||||||||||||||||
|
0 |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
||||||||
77. |
∫2 |
|
|
|
dx |
. |
|
78. |
+∞∫ |
ln x |
dx. |
79. |
+∞∫ |
|
|
dx |
. |
|
|||||||
|
2 |
|
|
|
|
|
x ln x |
|
|||||||||||||||||
|
0 x |
|
− 4x + 3 |
|
|
|
2 |
|
|
x |
|
|
|
2 |
|
|
|
|
|
||||||
№80–89.
80.Вычислить площадь фигуры, ограниченной линиями:
y2 = 2x +1, y − x +1 = 0.
81. Вычислить площадь фигуры, ограниченной линиями: y = x2 , x = y2 .
82. Вычислить площадь фигуры, ограниченной линиями: y2 +8x =16, y2 − 24x = 48.
83. Вычислить площадь фигуры, ограниченной линиями:
y = |
|
|
1 |
, y = |
x2 |
. |
|
1 |
+ x2 |
2 |
|||||
|
|
|
|||||
84.Вычислить площадь внутри кардиоиды r =1 − cos ϕ.
85.Вычислить длину кардиоиды r =1 − cos ϕ .
86.Вычислить длину одной арки циклоиды:
x= t −sin t, y =1 − cost , (0 ≤ t ≤ 2π).
87.Найти площадь поверхности, образованной вращением параболы y2 = 4x вокруг оси ox от вершины до x = 3.
88.Найти объем тела вращения параболы y2 = 4x, ограничен-
ной x =1 вокруг оси Ox.
89. Найти объем тела, ограниченного поверхностью вращения
эллипса |
x2 |
+ |
y2 |
=1 вокруг оси Ox. |
|
a2 |
b2 |
||||
|
|
|
7

III.Программа курса
1.Функции нескольких переменных
Определение функции нескольких переменных. Область определения функции. График функции двух переменных. Линии уровня функции двух переменных.
ε-окрестность точки на плоскости. Предел функции двух переменных. Основные теоремы о пределах для двух функций, имеющих пределы в данной точке. Бесконечно малая функция в точке. Непрерывность функции двух переменных. Полное приращение функции двух переменных в точке. Основные теоремы о непрерывных функциях двух переменных.
Частные производные функции двух переменных. Понятие дифференцируемости функции. Производная сложной функции. Дифференцирование функции, заданной неявно. Дифференциал функции двух переменных. Применение полного дифференциала в приближенных вычислениях. Касательная плоскость и нормаль к поверхности. Частные производные и дифференциалы высших порядков. Производная по направлению. Градиент функции.
Формула Тейлора для функции двух переменных. Определение локального минимума и локального максимума. Необходимое и достаточное условия экстремума функции двух переменных. Условный экстремум. Нахождение наибольшего и наименьшего значения функции двух переменных в замкнутой области.
2. Интегральное исчисление
Определение первообразной и неопределенного интеграла. Таблица основных интегралов.
Основные свойства неопределенного интеграла.
Метод замены переменной в неопределенном интеграле. Метод интегрирования по частям в неопределенном интеграле. Интегрирование рациональных выражений. Интегралы вида:
|
ax + b |
|
∫R (x, ax2 + bx + c )dx, ∫R(sin x,cos x)dx. |
|
∫R x, m |
dx, |
|||
cx + d |
||||
|
|
|
Определенный интеграл. Условие интегрируемости функций. Свойства определенного интеграла. Оценки определенных интегралов. Теорема о среднем для определенного интеграла.
8
Интеграл с переменным верхним пределом. Формула Ньюто- на-Лейбница. Замена переменных в определенном интеграле.
Площадь криволинейной трапеции. Площадь криволинейного сектора, ограниченного кривой, заданной в полярной системе координат. Вывод формулы вычисления длины дуги. Вывод формулы для вычисления объема по поперечным сечениям. Вывод формулы вычисления объема тела вращения. Вывод формулы вычисления площади поверхности вращения.
Физические приложения определенного интеграла: нахождение длины пройденного пути через скорость, определение работы, совершенной силой, нахождение давления жидкости.
Несобственные интегралы с бесконечными пределами интегрирования. Несобственные интегралы от неограниченных функций.
Приближенные способы вычисления определенного интеграла формулой прямоугольника, формулой трапеции, формулой Симпсона (парабол).
9
IV. Список рекомендуемой литературы |
|
V. Вопросы к экзамену |
|||||
1. Бугров, Я. С. Высшая математика. Т. 2. Дифференциальное |
1. |
Определение функции нескольких переменных. |
|||||
и интегральное исчисление / Я. С. Бугров, С. М. Никольский. – М. : |
2. |
Предел функции двух переменных. |
|||||
Дрофа, 2004. |
3. |
Непрерывность функции двух переменных. |
|||||
2. Дубовик, О. А. Математический анализ-I (дифференциаль- |
4. |
Свойства непрерывных функций двух переменных. |
|||||
ное исчисление функции одной переменной) : метод. пособие / |
5. |
Частные производные. |
|
|
|
||
О. А. Дубовик, П. И. Совертков. – Сургут : ИЦ СурГУ, 2008. |
6. |
Понятие дифференцируемости функции. |
|||||
3. Задачи и упражнения по математическому анализу для вту- |
7. |
Производная сложной функции. |
|||||
зов / под ред. Б. П. Демидовича. – М. : Наука, 1964–1978. |
8. |
Дифференциал функции двух переменных. |
|||||
4. Пискунов, Н. С. Дифференциальное и интегральное исчис- |
9. |
Касательная плоскость к поверхности. |
|||||
ление для втузов. Т. 1. / Н. С. Пискунов. – М. : Наука, 1985. |
10. |
Частные производные и дифференциалы высших порядков. |
|||||
5. Сборник задач по высшей математике. 1 курс / К. Н. Лунгу |
11. |
Производная по направлению. Градиент функции. |
|||||
[и др.]. – М. : Айрис-пресс, 2003. |
12. |
Формула Тейлора для функции двух переменных. |
|||||
6. Шипачев, В. С. Высшая математика / В. С. Шипачев. – М. : |
13. |
Необходимое условие экстремума. |
|||||
Высш. шк., 1996. |
14. |
Достаточное условие экстремума. |
|||||
|
15. |
Условный экстремум. |
|
|
|
||
|
16. |
Нахождение наибольшего и наименьшего значения функ- |
|||||
|
ции двух переменных в замкнутой области. |
||||||
|
17. |
Первообразная и неопределенный интеграл. |
|||||
|
18. |
Свойства неопределенного интеграла. |
|||||
|
19. |
Метод замены переменной. |
|||||
|
20. |
Метод интегрирования по частям. |
|||||
|
21. |
Интегрирование рациональных выражений. |
|||||
|
|
|
∫ |
|
|
ax + b |
|
|
|
|
|
|
|
|
|
|
22. |
Интеграл вида |
|
R x, m |
|
|
dx. |
|
|
|
|
|
|
cx + d |
|
|
23. |
Интеграл вида ∫R (x, |
ax2 + bx + c )dx. |
||||
|
24. |
Интеграл вида ∫R(sin x,cos x)dx. |
|||||
|
25. |
Определенный интеграл. |
|||||
|
26. |
Условие интегрируемости функций. |
|||||
|
27. |
Свойства определенного интеграла. |
|||||
|
28. |
Оценки определенных интегралов. |
|||||
|
29. |
Интеграл с переменным верхним пределом. |
|||||
|
30. |
Формула Ньютона – Лейбница. |
|||||
|
31. |
Замена переменных в определенном интеграле. |
|||||
|
32. |
Площадь криволинейной трапеции. |
|||||
10 |
|
|
|
|
11 |
|
|
33.Площадь криволинейного сектора, ограниченного кривой, заданной в полярной системе координат.
34.Вычисление длины дуги.
35.Вычисление объема по поперечным сечениям.
36.Вычисление объема тела вращения.
37.Вычисление площади поверхности вращения.
38.Несобственные интегралы с бесконечными пределами интегрирования.
39.Несобственные интегралы от неограниченных функций.
40.Приближенный способ вычисления определенного интеграла формулой трапеции.
41.Приближенный способ вычисления определенного интеграла формулой Симпсона (парабол).
42.Физические приложения определенного интеграла.
12
VI. Справочные материалы |
|
|||
Греческий алфавит |
|
|
|
|
Αα – альфа |
Ββ – бэта |
Γγ |
– гамма |
δ – дельта |
Εε – эпсилон |
Ζζ – дзета |
Ηη |
– эта |
Θθ – тета |
Ιι – йота |
Κκ – каппа |
Λλ |
– ламбда |
Μμ – мю |
Νν – ню |
Ξξ – кси |
Οο – омикрон |
Ππ – пи |
|
Ρρ – ро |
Σσ – сигма |
Ττ – тау |
Υυ – ипсилон |
|
Φϕ – фи |
Χχ – хи |
Ψψ – пси |
Ωω – омега |
|
Функция двух переменных
С2 [a;b] – класс функций, имеющих непрерывные производные до второго порядка включительно на отрезке [a; b].
С1[a;b] – класс функций, имеющих непрерывные производные первого порядка на отрезке [a; b].
С0 [a;b] – класс непрерывных функций на отрезке [a; b]. ε-окрестностью точки M0 (x0 ; y0 ) называется множество
{M (x; y)} всех точек, координаты которых удовлетворяют неравен-
ству (x − x0 )2 + ( y − y0 )2 < ε , т.е. открытый круг с центром в точке
M0 (x0 ; y0 ) и радиусом ε.
Точка А называется внутренней точкой множества Н, если существует ε-окрестность этой точки, содержащаяся в множестве Н
(рис. 1).
Точка В называется граничной точ- |
|
|
|
кой множества Н, если любая ее ε-ок- |
|
В |
|
рестность содержит как точки, принадле- |
|
||
|
|
||
жащие множеству Н, так и не принадле- |
|
|
|
жащие Н (рис. 1). |
А |
H |
|
Множество точек плоскости назы- |
|||
|
|
||
вается связным, если любые две точки |
|
|
|
этого множества можно соединить непре- |
|
|
|
рывной линией, состоящей из точек этого |
|
Рис. 1 |
|
множества. |
|
|
Множество, все точки которого являются внутренними точками для этого множества, называется открытым множеством.
13
Множество на плоскости называется замкнутым, если его дополнение – открытое множество.
Связное открытое множество точек называется открытой об-
ластью или просто областью.
Множество точек называется ограниченным, если существует круг, внутри которого оно содержится.
Число А называется пределом функции z = f (M ) в точке M0 , если для любой сходящейся к M0 последовательности точек M1, M2 , ..., Mn , ... ( Mn ≠ M0 ) соответствующая последовательность значений функции f (M1 ), f (M2 ), ..., f (Mn ), … сходится к А.
Обозначение lim f (M ) = A, |
lim f (x, y) = A. |
M →M0 |
x →x0 |
|
y → y0 |
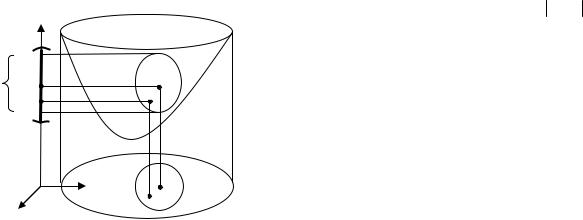
Число А называется пределом функции z = f (M ) в точке M0 , если для любого ε > 0 существует δ > 0, такое, что для всех точек M ≠ M0 , принадлежащих δ-окрестности точки M0 , значения функции f (M ) принадлежат ε-окрестности точки А.
На рис. 2 число А является пределом функции z = f (M ) в точке M0 , так как для любой ε-окрестности точки А, т.е. интервала (A − ε; A + ε) нашлась в области определения Df функции δ-окрест-
ность точки M0 , |
т.е. открытый круг Uδ , такой, что для всех то- |
||
чек M , принадлежащих Uδ , |
значения функции f (M ) принадлежат |
||
ε-окрестности точки A, т.е. f (Uδ ) (A − ε; A + ε) . |
|||
|
z |
|
z = f (x, y) |
|
A +ε |
|
|
|
|
|
|
f (Uδ) |
A |
|
|
|
f (M) |
|
|
|
A −ε |
|
|
|
О |
y |
M0 Uδ |
|
|
||
|
x |
|
M |
|
|
Df |
|
Рис. 2
14
Теорема. Пусть функции f (M ) и g(M ) определены на одном и том же множествеG и имеют в точкеM0 G соответственно преде-
лы А и В. Тогда функции f (M ) ± g(M ), f (M ) g(M ), f (M ) / g(M ),
B ≠ 0 имеют в точке M0 |
пределы, равные соответственно A ± B, |
A B, A/ B. |
|
Функция z = f (M ) |
называется непрерывной в точке M0 , если |
существует предел функции в этой точке, и он равен значению функции в точке M0 , т.е.:
lim f (M ) = f (M0 ) |
или lim f (x, y) = f (x0 , y0 ). |
M → M0 |
x →x0 |
|
y → y0 |
z = f (M ) − f (M0 ) = f (x + x, y + y) − f (x, y) – полное прира- |
|
щение функции z = f (M ) |
в точке M0 . |
Эквивалентное определение непрерывности функции в точке. |
|
Функция z = f (M ) |
называется непрерывной в точке M0 , если |
ее полное приращение в этой точке есть бесконечно малая функция
при M → M0 |
, т.е. lim |
z = 0 или lim z = 0. |
|
M →M0 |
x→x0 |
|
|
y→y0 |
Глобальные свойства непрерывных функций
1. Непрерывная функция z = f (M ) в замкнутой ограниченной
области ограничена в этой области, т.е. существует такое положительное число М, что для всех точек области выполняется следую-
щее неравенство: f (M ) ≤ M .
2. Непрерывная функция z = f (M ) в замкнутой ограниченной
области достигает своих точных граней.
3. Непрерывная функция z = f (M ) в области принимает все
промежуточные значения между любыми двумя своими значениями, т.е. если А и В какие-то значения функции f (M ) в данной облас-
ти и С – число, удовлетворяющее условию А< C < B, то в этой области существует точка M0 , в которой f (M0 ) = C.
zx′ = lim |
f (x + |
x, y) − f (x, y) |
– частная производная функ- |
|||||
|
|
|
|
|
||||
x → 0 |
|
|
x |
|
|
|
|
|
ции z = f (x, y) |
в точке (x, y) по переменной х. Другие обозначения |
|||||||
|
′ |
дf |
|
дz |
|
д |
||
этой производной: fx , |
|
, |
|
, |
|
f . |
||
дx |
дx |
дх |
||||||
|
|
|
|
|
15 |
|
||

f (x, y + y) − f (x, y)
y
ции z = f (x, y) в точке (x, y) по переменной y. Другие обозначения этой производной: fy′, ддfy , ддyz , ддy f .
Функция z = f (M ) называется дифференцируемой в точке М, если ее полное приращение в этой точке можно представить в виде
z = A x + B y + α( |
x, |
y) |
x +β( |
x, |
y) y , где А и В – неко- |
торые числа, не зависящие от |
x, |
y , а α( |
x, y) , β( x, y) – беско- |
||
нечно малые функции при |
x → 0, |
y → 0. |
|
||
Теорема. Если функция z = f (M ) |
дифференцируема в точке |
||||
М, то она непрерывна в этой точке. |
|
|
|||
Теорема. Если функция z = f (M ) |
дифференцируема в точке |
||||
M (x, y), то она имеет в этой точке частные производные fx′(x, y) и
fy′(x, y) , причем fx′(x, y) = A , |
fy′(x, y) = B. |
Теорема. Если функция |
z = f (M ) имеет частные производ- |
ные в некоторой окрестности точки М и эти производные непрерывны в самой точке М, то функция дифференцируема в точке М.
Теорема. Если функции x = x(t) и y = y(t) дифференцируемы в точке t, афункция z = f (x, y) дифференцируема вточке M (x(t), y(t)), то сложная функция z = f [x(t), y(t)] дифференцируема в точке t, причем производная сложной функции вычисляется по формуле:
|
dz |
|
= |
дz |
|
|
dx |
|
+ |
дz |
|
dy |
. |
|
|
|
|
|
|||||||
|
dt |
дx dt |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
дy dt |
|
|
|
|
|
|
||||||||||||||||
Аналогично для функции u = f [x(t), y(t), z(t)]: |
|||||||||||||||||||||||||
|
du |
= |
дu |
|
dx |
+ |
дu |
|
dy |
+ |
дu |
|
dz |
. |
|
||||||||||
|
dt |
дx dt |
дy dt |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
дz dt |
|
||||||||||||||||||
Теорема. Если функции x = x(u,v) и y = y(u,v) дифференци- |
|||||||||||||||||||||||||
руемы в точке M (u,v) , |
а функция z = f (x, y) |
дифференцируема в |
|||||||||||||||||||||||
|
|
|
′ |
где |
|
x = x(u,v) и y = y(u,v), то сложная функция |
|||||||||||||||||||
точке M (x, y) , |
|
||||||||||||||||||||||||
z = f [x(u,v), y(u,v)] |
дифференцируема в точке |
M (u,v), причем ча- |
|||||||||||||||||||||||
стные производные сложной функции вычисляются по формулам:
дz |
= |
дz |
|
дx |
+ |
дz |
|
дy |
, |
дz |
= |
дz дx |
+ |
дz |
|
дy |
. |
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
дu дx дu |
|
дy дu дv дx дv дy дv |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
Аналогично для сложной функции w = f [x(u,v), y(u,v), z(x, y)]:
ддwu = ддwx ддux + ддwy ддuy + ддwz ддuz , ддwv = ддwx ддxv + ддwy ддyv + ддwz ддvz .
Теорема. Если функция x = x(u,v) дифференцируема в точке M (u,v) , а функция z = f (x) дифференцируема в точке M ′(x) , где x = x(u,v) , то сложная функция z = f [x(u,v)] дифференцируема в точке M (u,v) , причем частные производные сложной функции вычисляются по формулам:
|
дz |
= |
dz |
|
дx |
, |
|
дz |
= |
dz |
|
дx |
. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
дu |
dx дu |
|
дv |
|
dx дv |
|
|
|
|||||||||
Дифференциалом |
|
dz |
дифференцируемой в |
точке М функ- |
||||||||||||||
ции z = f (M ) |
называется |
линейная часть полного |
приращения |
|||||||||||||||
этой функции в точке М относительно приращений |
x и |
y, т.е. |
||||||||||||||||
z = A x + B |
y, гдеАиВ– некоторыечисла, независящиеот |
x, y . |
||||||||||||||||
dz = fx′(x, y) |
x + fy′(x, y) y , dz = fx′(x, y) dx + fy′(x, y) dy |
– фор- |
||||||||||||||||
мулы для вычисления дифференциала в точке M (x, y) |
при заданных |
|||||||||||||||||
приращениях |
x, |
y переменных, где dx = x, dy = |
y. |
|
|
|||||||||||||
|
z ≈ fx′(x, y) |
|
x + fy′(x, y) y – формула для вычисления при- |
|||||||||||||||
ближенного значения приращения функции в точке M (x, y) |
при за- |
|||||||||||||||||
данных приращениях |
x, y переменных. |
|
|
|
||||||||||||||
|
z − z0 |
= fx′(x0 , y0 )(x − x0 ) + fy′(x0 , y0 )( y − y0 ) – |
уравнение каса- |
|||||||||||||||
тельной плоскости к поверхности, заданной уравнением z = f (x, y) в точке N(x0 , y0 , z0 ) поверхности, где z0 = f (x0 , y0 ).
n ( fx′(x0 , y0 ); fy′(x0 , y0 ); −1) – нормальный вектор к поверхности в точке N(x0 , y0 , z0 ).
|
x − x0 |
= |
y − y0 |
|
= |
z − z0 |
– уравнение нормали к поверх- |
|
fx′(x0 , y0 ) |
fy′(x0 , y0 ) |
−1 |
||||
|
|
|
|
||||
ности, заданной уравнением |
z = f (x, y) в точке N(x0 , y0 , z0 ) по- |
||||||
верхности, где z0 |
= f (x0 , |
y0 ). |
|
|
|||
Fx′(x0 , y0 , z0 )(x − x0 ) + Fy′(x0 , y0 , z0 )( y − y0 ) + Fz′(x0 , y0 , z0 )(z − z0 ) = 0 –
уравнение касательной плоскости к поверхности, заданной общим
17
уравнением F(x, y, z) = 0 |
в точке |
N(x0 , y0 , z0 ) |
поверхности, т.е. для |
||||||||||||||||||||||||
которой F(x0 , y0 , z0 ) = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
x − x0 |
|
|
|
|
|
|
y − y0 |
|
|
|
|
|
z − z0 |
|
– уравнение нормали. |
||||||||||
|
Fx′(x0 , y0 , z0 ) = Fy′(x0 , y0 , z0 ) = |
Fz′(x0 , y0 , z0 ) |
|||||||||||||||||||||||||
|
Производная функции |
|
z = f (M ) |
|
в точке |
M (x, y) в направ- |
|||||||||||||||||||||
лении вектора l : |
|
|
|
|
f (M1 ) − f (M ) |
|
|
|
|
|
|
||||||||||||||||
|
дz |
= lim |
|
|
z |
= |
|
lim |
, |
|
|
y |
|
|
|||||||||||||
|
дl |
|
|
l |
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
l → |
0 |
|
|
|
M1 |
→ M |
|
|
|
|
|
|
|
|
|
|
|
|
|
M1 |
|||||
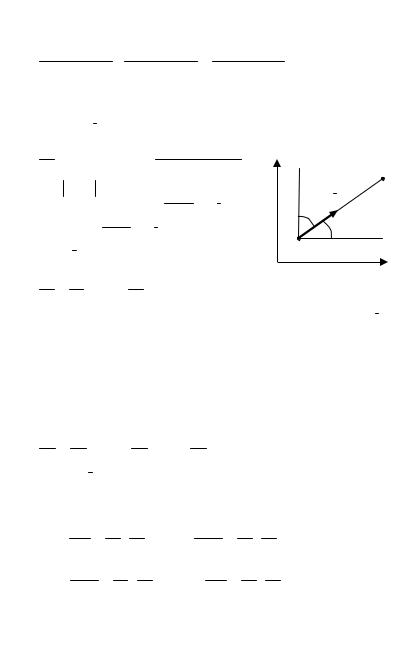
где |
l = ± MM1 |
|
, т.е. длина отрезка MM1 , |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
l |
||||||||||||||||||||||
взятая со знаком (+), если MM1 ↑↑ l и со |
|
|
|
β |
|||||||||||||||||||||||
знаком (–), если MM1 ↑↓ l (рис. 3). |
|
|
|
|
|
|
|
|
|
α |
|||||||||||||||||
|
|
|
|
|
|
|
M |
|
|
||||||||||||||||||
|
Если l(cos α; cosβ), то |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
дz |
|
дz |
|
|
|
|
|
|
|
дz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3 |
|
|
дl |
= |
дx cos α + |
дy cosβ |
|
– |
формула |
|
|
|
|
|
|||||||||||||||
для вычисления производной функции в направлении вектораl. |
|||||||||||||||||||||||||||
|
grad z = (zx′; z′y ) |
|
– градиентфункции z = f (M ) в точке M (x, y). |
||||||||||||||||||||||||
|
Градиент функции z = f (M ) |
|
в точке M (x, y) |
характеризует |
|||||||||||||||||||||||
направление и величину максимальной скорости возрастания этой |
|||||||||||||||||||||||||||
функции в данной точке. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Для функции u = f (x, y, z) : |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
дu |
= |
дu cos α + |
дu cosβ + дu cos γ, где α, β, γ – углы, образован- |
|||||||||||||||||||||||
|
дl |
|
дx |
|
|
|
|
|
|
дy |
|
|
дz |
|
|
|
|
|
|
|
|
|
|
|
|||
ные вектором l соответственно с координатными осями Ox, Oy, Oz, |
|||||||||||||||||||||||||||
grad u = (ux′; u′y ; uz′ ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
′′ |
= |
д2 z |
= |
д |
|
дz |
′′ |
= |
д2 z |
|
= |
|
д дz |
, |
|
|
||||||||||
|
zxx |
дx |
2 |
дх |
|
|
|
, zxy |
дyдx |
дy |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
дx |
|
|
|
|
дx |
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
|
z′′yx |
= |
д z |
|
|
= |
д |
дz |
z′′yy |
= д z2 = |
|
д |
производные вто- |
||||||||||||||
|
|
|
|
, |
|
|
дz – |
||||||||||||||||||||
|
|
|
дxдy |
|
|
дx |
|
дy |
|
|
|
дy |
|
|
|
дy |
дy |
|
|
||||||||
рого порядка от функции z = z(x, y). |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
||
Если производные z′′xy (x, y) , z′′yx (x, y) существуют в некоторой окрестности точки M (x, y) и непрерывны в самой точке М, то в этой точке zxy′′ = z′′yx .
|
|
d 2 z = δ(dz) |
δx = dx, δy = dy – дифференциал |
второго |
порядка |
от |
||||||||||||||||||||||
функции z = z(x, y). |
|
|
′′ |
|
|
|
′′ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
2 |
|
′′ |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
d |
z = zxx (dx) |
+ 2zxy dxdy + zyy (dy) |
– |
выражение второго диф- |
||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
ференциала функции z = z(x, y) |
|
через дифференциалы независимых |
||||||||||||||||||||||||||
аргументов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Аналогично: |
|
|
|
|
|
′′ |
|
|
|
|
′′ |
|
|
|
|
′′ |
|
′′ |
|
|
||||||
|
2 |
′′ |
|
2 |
|
|
′′ |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||
d |
u = uxx (dx) |
+ uyy (dy) |
+ uzz (dz) |
+ 2uxy dxdy |
+ 2uxz dxdz |
+ 2uyz dydy |
|
– |
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
выражение второго дифференциала функции u = u(x, y, z) . |
|
|
||||||||||||||||||||||||||
|
f |
= df (x, y) + |
d 2 f (x, y) |
+ ... + |
d n f (x, y) |
+ |
d n +1 f (x + θ x, y + θ y) |
, |
||||||||||||||||||||
|
|
|
2! |
|
|
|
|
|
|
n! |
|
|
|
|
|
(n +1)! |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где 0 < θ <1 – формула Тейлора для функции z = f (x, y). |
|
|
||||||||||||||||||||||||||
|
|
Функция z = f (x, y) имеет в точке M0 (x0 , y0 ) |
локальный мак- |
|||||||||||||||||||||||||
симум (минимум), |
если существует такая окрестность точки M0 , в |
|||||||||||||||||||||||||||
которой для любой точки M (x, y) |
выполняется неравенство: |
|
|
|||||||||||||||||||||||||
|
|
f (x, y) ≤ f (x0 , y0 ) |
|
|
( f (x, y) ≥ f (x0 , y0 )). |
|
|
|
|
|||||||||||||||||||
|
|
Точки локального максимума и локального минимума назы- |
||||||||||||||||||||||||||
ваются точками экстремума. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
На рис. 4 точки |
M0 , |
|
M1 являются точками |
экстремума |
|||||||||||||||||||||
функции, но точка M2 |
не является точкой экстремума (почему?). |
|
|
|||||||||||||||||||||||||
|
|
|
Необходимое условие экстремума. Если функция z = f (x, y) |
|||||||||||||||||||||||||
имеет в точке |
|
M0 (x0 , y0 ) |
экстремум и имеет в точке |
M0 частные |
||||||||||||||||||||||||
производные |
|
первого |
порядка, |
|
то в |
|
этой |
точке |
fx′(x0 , y0 ) = 0 |
|
и |
|||||||||||||||||
fy′(x0 , y0 ) = 0.
Точка, в которой выполняется условие fx′(x0 , y0 ) = 0 и fy′(x0 , y0 ) = 0 называется точкой возможного экстремума (стацио-
нарной точкой).
19
