
Дубовик О.А., Совертков П.И
.pdf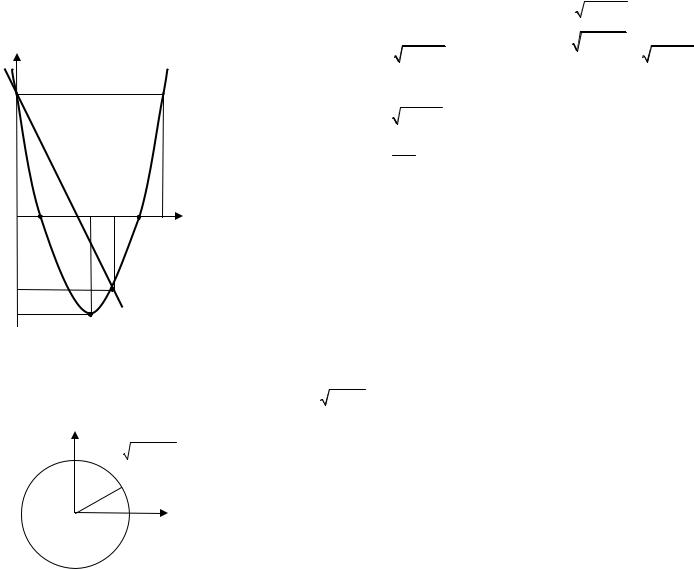
XI. Основные направления применения интеграла
1. Вычисление площади плоской фигуры
Пример 22. Найти площадь фигуры, ограниченной параболой y = x2 − 6x + 5 и прямой y = 5 − 2x.
|
Решение. Построим пара- |
у |
|
болу |
y = x2 − 6x + 5 и прямую |
||
|
y = 5 − 2x (рис. 18). Найдем точки пересечения этих линий:
|
2 |
− 6x |
+ 5 |
у = x |
|||
|
|
|
|
y = 5 − 2x |
. |
||
Из уравнения |
|||
x2 − 6x + 5 = 5 − 2x |
найдем абс- |
||
циссы точек пересечения линий: x = 0, x = 4 . Значит, рассматри-
ваемая фигура F ограничена слева прямой x = 0, справа – прямой
x = 4, сверху прямой y = 5 − 2x и снизу параболой y =x2 −6x+5.
Для определения площади вычислим интеграл:
5 
3 |
4 |
О 1 F |
5 6 х |
– 3
– 4
Рис. 18
4 |
2 |
4 |
2 |
|
|
2 |
|
x3 |
|
4 |
|
2 |
|
|
|
|
|
|
|
||||||||||
S = ∫((5 − 2x) − (x |
|
− 6x + 5)) dx =∫(4x − x |
|
) dx = |
2x |
|
− |
|
|
|
|
=10 |
|
. |
|
|
|
3 |
|
0 |
3 |
||||||||
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
||
2. Вычисление длины линии
Пример 23. Найти длину окружности с радиусом R.
Первый способ. Выберем пря-
моугольную декартову систему координат, начало которой совпадает с центром окружности (рис. 19), тогда окружность имеет уравнение
x2 + y2 = R2 .
Это уравнение не задает график функции, так как одному и тому же значению аргумента х соответствует два значения у, которые можно опре-
60
у
B |
y = R 2 − x 2 |
R
ОA х
Рис. 19
делить из уравнения. На линии выделим участок, который однозначно проектируется на ось Ox. Например, для четверти окружно-
сти, т.е. дуги АВ, найдем ее уравнение y = |
R2 − x2 |
, |
где x [0; R]: |
|||||||||||||||||||||||||
|
′ |
|
|
|
x |
′ |
2 |
|
|
|
|
|
|
x2 |
|
|
|
|
′ 2 |
|
|
|
R2 |
|
|
|||
y |
|
= − |
|
|
, ( y ) |
|
= |
|
|
|
, |
|
1 + |
( y ) |
= |
|
|
. |
||||||||||
|
R2 − x2 |
|
R2 − x2 |
|
|
R2 − x2 |
||||||||||||||||||||||
Длина окружности равна: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
l = 4 |
R |
R dx |
= 4R arctg |
x |
|
|
R |
= 4R |
|
|
R |
|
|
|
|
4R |
π |
, l = 2πR. |
||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
arctg |
|
|
−0 |
|
= |
|
|||||||||||||
∫0 |
|
|
R |
|
|
R |
2 |
|||||||||||||||||||||
|
|
|
R2 − x2 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Второй способ. Пусть для произвольной точки |
M окружно- |
|||||||||||||||||||||||||||
сти вектор OM образует с осью Ox угол t, тогда для координат этой точки получаем x = R cost, y = R sin t. Это параметрические уравнения окружности. Для четверти окружности угол t изменяется от 0 до π/ 2. В этом случае вычисление длины дуги значительно упрощается:
x′ = −R sin t, y′ = R cost,
π
2 |
π |
x′2 + y′2 = R2 , l = 4∫R dt = 4Rt |
02 = 2πR. |
0 |
|
Третий способ. Рассмотрим полярную систему координат, полюс которой совпадает с центром окружности. Для окружно-
сти получаем полярное |
уравнение r = R = const, тогда r′ = 0, |
|
π |
|
|
2 |
|
π |
r + r′2 = R и l = 4∫R dϕ = 4Rϕ |
02 = 2πR. |
|
0 |
|
|
3. Вычисление объема тела вращения
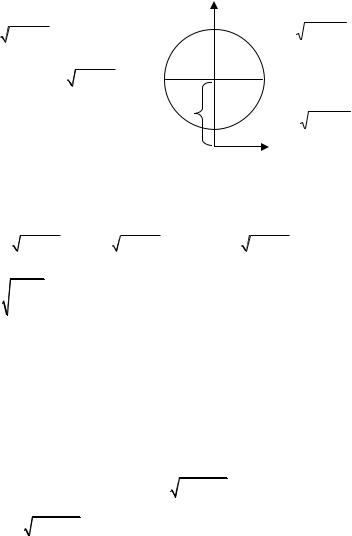
Пример 24. Тором называется тело, полученное при вращении круга радиуса r вокруг оси, лежащей в его плоскости на расстоянии a от центра круга, где a > r. Вычислить объем тора.
Для системы координат, выбранной на рис. 20, уравнение окружности имеет вид x2 + ( y − a)2 = r2 .
61
|
|
|
Верхняя |
|
|
|
полуокруж- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
ность ABC имеет уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
y |
= a + |
|
r2 − x2 , |
|
|
|
|
а |
нижняя |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 |
= a + |
r 2 − x 2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
полуокружность CDA имеет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
уравнение y2 |
= a − |
|
r2 − x2 . |
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
Объем тора равен раз- |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
ности объемов тел, получен- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
= a − |
r 2 − x 2 |
|||||||||||||||||||||||||||||||||||||||||
ных |
при |
|
вращении |
|
|
этих |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
полуокружностей, поэтому: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
V = π∫r |
y12 (x) dx − π∫r |
y22 (x) dx = π∫r |
|
|
|
|
Рис. 20 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
( y12 (x) − y22 (x)) dx = |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
−r |
|
|
|
|
|
|
) |
|
|
|
|
|
|
−r |
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
−r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
r |
|
|
+ |
r |
2 |
− x |
2 |
2 |
−(a − |
|
|
|
r |
2 |
− x |
2 |
2 |
|
|
|
|
|
|
|
|
r |
|
r |
2 |
− x |
2 |
|
dx = |
|||||||||||||||||||||||||||||
= π∫ |
(a |
|
|
|
|
|
|
|
|
|
|
|
|
dx = 4πa ∫ |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
−r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 4πar ∫ |
|
1 − x2 |
dx = |
|
|
|
|
x |
|
= cost |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
dx r |
|
|
|
|
|
= −4πar∫r sin2 t dt = |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
r |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−r |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
= −sin t dt |
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 0 |
1 − cos 2t |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
sin 2t |
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
= −4πar |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
dt = −πar |
|
|
t |
− |
|
|
|
|
|
|
|
. V = |
2π |
|
ar |
|
. |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
4. Вычисление площади поверхности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Пример 25. Найти площадь поверхности, образованной |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вращением одной |
арки |
|
|
циклоиды |
|
|
x = a(t −sin t), y = a(1 − cost), |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
t [0; 2π] вокруг оси Ox . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
Решение. x′ = a − a cost, y′ = a sin t, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
x |
′2 |
+ y |
′2 |
|
= |
2a |
2 |
(1− cost) = 4a |
2 |
|
sin |
2 t |
|
|
, |
|
x |
′2 |
+ y |
′2 |
= 2a sin |
t |
|
, |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
P = 2π2∫π y(t) |
|
|
x′2 + y′2 dt = 2π2∫π a(1− cost)2asin |
t |
|
dt = |
8πa2 |
2∫πsin3 |
t |
dt = |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
|
|
|
|
|
|
|
2 |
2π |
|
|
2 |
|
t |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2π |
|
|
|
|
|
|
2 t |
|
|
|
|
t |
|
|
|
|
|||||||||||||||
= −16πa |
|
∫ |
sin |
|
|
|
|
d |
cos |
|
|
|
= −16πa |
∫ |
1 − cos |
|
|
|
d cos |
|
|
|
|
= |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
2 |
|
2 |
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= −16πa |
2 |
|
|
|
|
t |
|
|
1 |
|
|
|
|
3 t |
|
2π |
|
|
|
|
64πa2 |
, |
|
P |
|
64πa2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
cos |
|
|
− |
|
|
|
|
cos |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
5. Доказательство равенств |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
Пример 26. Доказать, что для любых чисел x1 , x2 , |
удовлетво- |
||||||||||||||||||||||||||||||||||||||||||||||||||
ряющих условию |
|
x1 |
|
|
<1, |
|
x2 |
|
<1, |
выполняется равенство: |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
arctg x |
+ arctg x |
|
|
= arctg |
x1 + x2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 − x1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + x2 |
|
|
|
|||||||||||||
|
|
|
Решение. Рассмотрим |
функцию |
F(x) = arctg |
|
, |
тогда |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − xx |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
′ |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
x + x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
F (x) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
1 − xx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
1 + |
|
x + x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
1 − xx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
|
|
(1 − xx )2 |
|
|
|
|
|
|
|
|
(1 − xx ) − (x + x )(−x ) |
|
= |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
(1 |
− xx )2 |
+ |
(x + x |
)2 |
|
|
(1 |
− xx |
|
)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 + x |
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
′ |
|
1 |
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= (1 + x2 ) (1 + x2 ) = 1 + x2 , т.е. F (x) |
= 1 + x2 |
= |
(arctg x) . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функции F(x) и arctg x |
имеют равные производные, следова- |
||||||||||||||||||||||||||||||||||||||||||||||||||
тельно, они являются первообразными для функции |
|
|
1 |
|
|
и эти |
||||||||||||||||||||||||||||||||||||||||||||||||
1 |
+ x2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
первообразные |
отличаются |
|
на |
|
|
|
постоянную |
величину, |
т.е. |
|||||||||||||||||||||||||||||||||||||||||||||
F(x) = arctg x + C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Полагая в этом равенстве x = 0 и учитывая arctg 0 = 0 , полу- |
|||||||||||||||||||||||||||||||||||||||||||||||||||
чаем arctg x |
= C. Значит arctg |
|
x + x2 |
|
|
= arctg x + arctg x . При x = x |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − xx2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|||||||||||
|
|
|
|
|
|
|
|
|
x1 + x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
получаем arctg |
|
|
= arctg x + arctg x . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 − x1 x2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Замечание. |
Областью значений функции y = arctg x является |
||||||||||||||||||||||||||||||||||||||||||||||||||
множество |
|
|
− π; |
π . |
|
|
|
Ограничения |
|
|
x |
|
<1, |
|
x |
|
|
|
<1 |
обеспечивают вы- |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
полнение неравенств |
|
|
|
− π < arctg x |
|
< π, − |
π < arctg x < π |
, а значит |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
1 |
|
4 |
4 |
|
|
|
|
1 |
|
4 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
− π < arctg x + arctg x |
|
|
|
< π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
2 |
|
|
|
1 |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
63 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
6. Доказательство неравенств |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
Пример 27. Доказать неравенства: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
а) |
|
1 |
|
< ln |
|
48 |
< |
|
1 |
|
|
; |
б) |
1 |
< arcsin 0,8 − arcsin 0,6 < |
1 |
; |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
48 |
|
47 |
47 |
|
4 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
в) sin 200 |
< |
7 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
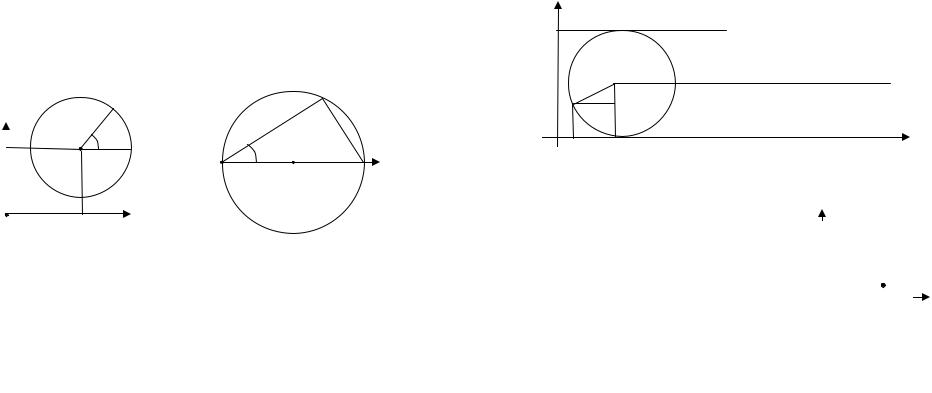
Решение. а) |
ln |
48 |
= ln 48 − ln 47 = ln x |
|
4748 = |
48∫ |
dx |
|
– площадь кри- |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
47 |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
47 x |
|
|
|
|
|
|
|
|
|
|
||||||
волинейной трапеции, ог- |
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
раниченной |
сверху |
|
гра- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||||||
фиком |
|
|
|
функции |
y = |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
x |
О |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
осью Ox, |
|
|
|
|
|
|
|
47 |
|
|
|
|
|
|
|
48 |
|
|
|
|
|
||||||||||||||||||||
снизу |
|
|
|
|
|
слева |
|
|
|
|
|
|
|
|
х |
|
|
|
||||||||||||||||||||||||||||||||
прямой |
|
|
|
|
x = 47, |
справа |
|
|
|
|
|
|
|
Рис. 21 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
прямой x = 48 (рис. 21). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
Справедливость неравенства |
очевидна, |
если |
заметить, что |
||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
и |
|
|
|
1 |
|
|
|
– площади прямоугольников с основанием, равным еди- |
||||||||||||||||||||||||||||||||||||||
48 |
|
47 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
нице, |
|
|
|
|
причем |
|
|
|
|
графики |
|
функций |
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
5 |
|
|
|
F |
|
|
|
|
|
|||||||||
|
y = |
48 |
, |
|
|
|
|
y = |
x |
|
, y |
= |
47 |
. |
на |
отрезке |
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
[47; 48] |
|
|
|
|
|
удовлетворяют |
|
условию |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
1 |
|
≤ |
1 |
|
|
≤ |
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
D |
|
|
E |
|
|
|
||||||
48 |
|
x |
|
|
47 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
б) Разность арксинусов предста- |
1 |
|
y = |
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
вим в виде определенного интеграла: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
arcsin 0,8 − arcsin 0, 6 = |
|
|
|
|
|
|
|
|
|
|
1 − x2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0,60,8 |
0,8 |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= arcsin x |
|
= ∫ |
|
|
|
|
|
|
|
|
|
– площадь S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,6 1 − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
криволинейной трапеции ABCD, ог- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
раниченной сверху графиком функции |
|
|
|
|
|
|
|
|
A |
|
|
|
B |
|
|
|
||||||||||||||||||||||||||||||||||
|
f (x) = |
|
|
|
|
|
1 |
|
|
(рис. 22). |
|
|
|
|
|
|
|
О |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,6 |
|
0,8 |
х |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 − x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Рис. 22
64
Вычислим |
f (0,6) = |
5 |
, f (0,8) |
= |
5 |
|
, тогда площадь |
прямо- |
|||||||||||||||||||||||||||||||
4 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||
угольника |
|
ABED равна S |
= 0,2 |
5 |
= |
1 |
, |
|
|
а площадь прямоугольника |
|||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ABCF |
равна |
|
S2 |
= 0,2 |
|
|
= |
|
. |
|
|
На |
|
|
отрезке |
[0,6; 0,8] |
функция |
||||||||||||||||||||||
|
|
3 |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
f (x) = |
|
|
|
|
непрерывна и монотонно возрастает, поэтому вы- |
||||||||||||||||||||||||||||||||||
|
1 − x2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
полняется неравенство |
|
5 |
≤ |
|
|
1 |
|
|
|
≤ |
5 |
, |
|
следовательно, выполняется |
|||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
3 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − x2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
неравенство S1 < S < S2 |
|
|
и искомое неравенство доказано. |
|
|
|
|||||||||||||||||||||||||||||||||
в) |
Представим |
|
sin 200 |
как |
площадь |
криволинейной тра- |
|||||||||||||||||||||||||||||||||
пеции |
OACD |
|
(рис. |
23): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у |
|
|
|
|
|
|
|
B |
|
|
|
|
||||
sin 200 = sin π = |
∫9 cos x dx. |
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
9 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = cos x |
||||
Площадь |
|
|
прямо- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
угольника |
|
OABD |
равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
π. Из неравенства |
π < |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
9 |
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
следует |
искомое неравен- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
||||||||||||||||
ство sin 20 |
0 |
7 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
О |
|
|
|
|
|
|
π |
|
|
|
|
π х |
||||||||||
|
< |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
2 |
|
||||||||||||||||
Рис. 23
65
XII. Некоторые линии
(x − x0 )2 + (y − y0 )2 = R2 – уравнение окружности с центром
M0 (x0 ; y0 ) и радиусом R . |
|
x = x0 + R cost, y = y0 + R sin t |
– параметрические уравнения |
окружности с центром M0 (x0 , y0 ) |
и радиусом R (рис. 24). |
ρ = 2R cos ϕ – полярное уравнение окружности с центром на полярной оси и проходящей через полюс системы координат (рис. 25).
x2 |
+ |
y2 |
=1 – каноническое уравнение эллипса с полуосями |
|
a2 |
b2 |
|||
|
|
a, b, центр которого находится в начале координат.
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
y0 |
|
|
|
|
|
|
|
t |
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
R |
|
|
O |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
R |
R |
ρ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
O |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Рис. 24 |
|
|
|
|
Рис. 25 |
|
|
|||||
Параметрические |
|
уравнения |
этого |
|
эллипса: |
x = a cost, |
||||||||||
y = bsin t, |
t [0; 2π]. |
|
|
|
|
|
|
|
||||||||
|
(x − x )2 |
|
|
|
( y − y )2 |
|
|
|
|
|
||||||
|
|
|
|
0 |
|
|
+ |
|
0 |
|
=1 – каноническое |
уравнение |
эллипса с |
|||
|
|
a2 |
|
|
b2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
полуосями a, b, |
центр которого находится в точке M0 (x0 ; y0 ). |
|
||||||||||||||
Параметрические |
|
уравнения |
этого эллипса: x = x0 + a cost, |
|||||||||||||
y = y0 + bsin t, t [0;2π]. |
|
|
|
|
|
|
|
|||||||||
|
x2 |
− |
y2 |
|
=1 – каноническое уравнение гиперболы. |
|
|
|||||||||
|
a2 |
b2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
66 |
|
|
|
|
|
|
Параметрические уравнения гиперболы:
x = a cht, y = b sht, t R для правой ветви, x = −a cht, y = b sht, t R для левой ветви.
Циклоидой называется траектория точки, лежащей на окружности радиуса R, которая катится без скольжения по прямой
(рис. 26).
Параметрические уравнения циклоиды: x = Rt − R sin t, y = R − R cost.
y 2R
|
C |
|
|
M |
t |
|
|
N |
|
|
|
y |
|
|
|
|
|
x |
|
O x |
H |
|
2πR |
|
|
|
Рис. 26 |
Астроидой |
называется |
y |
|
траектория точки, лежащей на |
|||
окружности радиуса R, кото- |
|
||
рая катится |
по |
внутренней |
|
стороне другой |
окружности |
|
|
|
|||
радиуса 4R (рис. 27). |
|
|
M |
|
|||
Параметрические |
урав- |
|
|
||||
O |
4R |
x |
|||||
нения астроиды: |
|
|
|||||
|
|
|
|
|
|||
x = 4R cost, y = 4Rsin t. |
|
|
|
|
|||
Общее |
уравнение |
аст- |
|
|
|
||
2 |
2 |
2 |
|
|
|
|
|
роиды: x3 + y3 = R3 .
Кардиоидой называется |
Рис. 27 |
траектория точки, лежащей на |
|
окружности радиуса R, кото- |
|
рая катится по внешней стороне окружности такого же радиуса
(рис. 28).
67
ρ = 2R(1 − cos ϕ) – полярное уравнение кардиоиды.
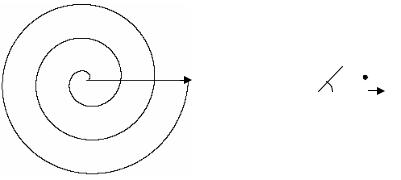
Спиралью Архимеда называется траектория точки, участвующей в равномерном вращении вокруг точки О с постоянной угловой скоростью и в равномерном движении вдоль прямой из точки О с постоянной линейной скоростью (рис. 29).
|
ρ |
M |
|
O |
φ |
|
|
O R |
ρ |
||
|
Рис. 28 Рис. 29
Полярное уравнение спирали Архимеда ρ = aϕ, где a – коэффициент пропорциональности, а ϕ – полярный угол.
|
68
Учебное издание
Дубовик Олег Андреевич Совертков Петр Игнатьевич
МАТЕМАТИЧЕСКИЙ АНАЛИЗ-II (функции нескольких переменных,
интегральное исчисление функции одной переменной)
Методическое пособие для студентов заочного отделения
Корректор Д.В. Вейраух
Верстка В.В. Чечевиной
Технический редактор В.В. Чечевина
Подписано в печать 26.06.2009 г. Формат 60×84/16. Усл. печ. л. 4,0. Уч.-изд. л. 3,4. Тираж 300. Заказ № 90.
Оригинал-макет подготовлен в редакционно-издательском отделе издательского центра СурГУ.
Тел. (3462) 23-25-75.
Отпечатано в полиграфическом отделе издательского центра СурГУ.
г. Сургут, ул. Лермонтова, 5. Тел. (3462) 32-33-06.
ГОУ ВПО «Сургутский государственный университет ХМАО – Югры» 628400, Россия, Ханты-Мансийский автономный округ,
г. Сургут, пр. Ленина, 1.
Тел. (3462) 76-29-00, факс (3462) 76-29-29.
69
