Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сургутский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Дубовик О.А., Совертков П.И

.pdf

Скачиваний:

Добавлен:

13.05.2015

Размер:

693.69 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

M0	M1
	M2

Рис. 4

Достаточные условия экстремума. Пусть M0 (x0 , y0 ) – точ-

ка возможного экстремума функции z = f (x, y) и в некоторой окрестности этой точки существуют непрерывные частные производ-

ные второго порядка.	Обозначим	fxx′′(x0 , y0 ) = A, fxy′′(x0 , y0 ) = B,
fyy′′(x0 , y0 ) = C.
Если AC − B2 > 0,	то в точке	M0 функция имеет экстремум,

причем при A < 0 – локальный максимум, при A > 0 – локальный минимум. Если AC − B2 < 0, то в точке M0 нет экстремума.

При AC − B2 = 0 требуется дополнительное исследование. Для некоторых функций экстремум существует, а для некоторых не существует.

Функция z = f (x, y) имеет в точке M0 (x0 , y0 ) на линии связи, заданной уравнением ϕ(x, y) = 0 условный максимум (условный ми-

нимум), если существует такая окрестность этой точки, что для всех точек М на линии связи ϕ(x, y) = 0 выполняется неравенство

f (M ) ≤ f (M0 ) (соответственно f (M ) ≥ f (M0 ).

Для нахождения условного экстремума составим функцию Лагранжа:

u(x, y,λ) = f (x, y) + λϕ(x, y), где λ – множитель Лагранжа.

Координаты точек возможного экстремума определяются из системы:

fx′(x, y) + λ ϕ′x (x, y) = 0,

′

(x, y) + λ ϕy (x, y) = 0,

ϕ(x, y) = 0.

Пусть

(x0 , y0 , λ0 )

– решение системы, тогда функция f (M )

достигает условный максимум в точке

M0 (x0 , y0 ),

если для диф-

ференциалов

dx,

dy,

удовлетворяющих условиям

ϕ′x (x0 , y0 )dx +

+ϕ′y (x0 , y0 )dy = 0

и (dx)2 + (dy)2 ≠ 0,

второй дифференциал функции

Лагранжа

отрицателен, т.е.

d 2u(x ,

, λ

, dx, dy) < 0 и

функция

f (M ) достигает

условный

минимум,

если при

этих

условиях

d 2u(x , y , λ

, dx, dy) > 0.

Чтобы найти наибольшее и наименьшее значение функции в замкнутой области, надо:

1)найти стационарные точки и вычислить в них значения функции;

2)найти наибольшее и наименьшее значение функции на линиях, образующих границу области;

3)из всех найденных значений выбрать наибольшее и наименьшее значение.

Интегральное исчисление функции одной переменной

∫ f (x) dx = F(x) + C,	′
	F (x) =f (x), F(x) – первообразная для f (x)

1) определение первообразной для функции y = f (x) и опре-

деление неопределенного интеграла.

Если F(x) – первообразная для функции f (x), то любая другая первообразная для f (x) имеет видF(x) + C, где C − const.

Дифференцирование и интегрирование – две взаимно-обрат-

ные операции: (∫ f (x) dx)′ = f (x) , ∫ f ′(x) dx = f (x) + C.

∫(cf (x))dx = c∫ f (x)dx, ∫( f + g )dx = ∫ fdx + ∫gdx, где c − const.

свойства неопределенного интеграла.

Таблица интегралов

∫0 dx = C,

∫dx = x + C,

∫xn dx =

xn+1

+ C, n ≠ −1,

∫

= −

+ C,

n +1

∫

= 2 x + C,

∫ex dx = ex + C,

∫ax dx =

+ C,

ln a

∫

= ln

+ C,

∫cos x dx = sin x + C,

∫sin x dx = −cos x + C,

∫tg x dx = −ln

cos x

+ C,

∫ctg x dx = ln

sin x

+ C,

∫

= tg x + C,

∫

= −ctgx + C,

cos

sin

∫

= arcsin

+ C, a > 0,

∫

= −arccos

+ C, a > 0,

− x

∫

arctg

+ C, a ≠ 0,

∫

= −

arc сtg

+ C, а ≠ 0,

+ x

∫

x − a

∫

+ C, a ≠ 0,

= ln

x + x2 + a

+ C,

− a

x + a

∫sh x dx = ch x + C,

∫ch x dx = sh x + C,

∫th xdx = ln

ch x

+ C,

∫cth x dx = ln

sh x

+ C,

∫

= th x + C,

∫

= −cth x + C.

ch x

sh x

∫u dv = uv − ∫v du – интегрирование по частям.

Если x = ϕ(t),

то ∫ f (x)dx = ∫

′

f (ϕ(t)) ϕ

(t) dt – интегрирование

заменой переменной:

′

–

интегрирование методом под-

∫ f (ϕ(t)) ϕ

(t) dt = ∫ f (ϕ) dϕ

ведения под знак дифференциала.

P(x)

Интегрирование правильных рациональных дробей

Q(x)

а) разложение знаменателя на множители:

Q(x, y) = (x − a)m (x2 + p x + q)n ;

б) запись дроби в виде:

P(x)

+... +

B1 x + C1

Q(x)

(x − a)m

(x − a)m−1

x − a

(x2

+ px + q)n

B2 x + C2

+... +

Bn x + Cn

(x2

+ px + q)n−1

x2 + px + q

Интегрирование иррациональных выражений:

а)

если

корни

подынтегральном

выражении

имеют вид

n xm , q x p ,

то оно преобразуется в рациональную дробь подстанов-

кой x = tk ,

где k – НОК показателей корней n, q;

б) если подынтегральное выражение содержит только корни

n (ax + b)m , q (ax + b)p ,

то оно преобразуется в рациональную дробь

подстановкой ax + b = tk ,

где k – НОК показателей корней n, q;

в) если подынтегральное выражение содержит только корни

ax + b m

ax + b

, q

то оно преобразуется в рациональную дробь

cx + d

подстановкой

ax + b

= tk ,

где k – НОК показателей корней n, q;

cx + d

г) пусть подынтегральное выражение является дифференци-

альным биномом, т.е.

имеет вид

xm (a + bxn )p dx , где m, n, p – ра-

циональные числа:

-если p Z, то x = ts , s – НОК знаменателей дробей т и п;

-если mn+1 Z , то подстановка a + bxn = ts , s – знаменатель дроби р;

-если mn+1 + p Z , то подстановка ax−n + b = ts , s – знамена-

тель дроби р.

Интегрирование тригонометрических выражений:

Неопределенные	интегралы	вида	∫sin ax sin bx dx,
∫sin ax cosbx dx, ∫cos ax	cosbx dx с	помощью	тригонометриче-
ских формул:
	23

sin αsin β = cos(α −β) − cos(α +β) , 2

cos αcosβ = cos(α −β) + cos(α +β) , 2

sin αcosβ = sin(α +β) + sin(α −β) приводятся к интегралам: 2

∫sin kx dx = −	cos kx	+ C, ∫cos kx dx =		sin kx	+ C.
	k			k

Неопределенные интегралы			вида		Im, n = ∫sinm x cosn x dx, где

m и n – натуральные числа находятся с помощью следующих замен:

а) если m и n – четные числа, то:
sin2 x =	1 − cos 2x	, cos2	x =	1 + cos 2x	, sin x cos x =	sin 2x	;
	2			2
					2

б) если хотя бы одно из чисел m и n – нечетное, то от нечетной степени отделяется множитель и вводится под дифференциал. Например:

Im, 2k + 1 = ∫sinm x cos2k + 1 x dx = ∫sinm x cos2k x cos x dx =

= ∫sinm x (1 −sin2 x)k d(sin x) = (sin x = t ) = ∫tm (1 −t2 )k dt – сводится к интегралу от многочлена.

Интеграл вида ∫R(sin x, cos x) dx, где R(sin x, cos x) – рацио-

нальная функция от sin x и cos x с помощью замены tg 2x = t приво-

				2t		1 −t	2	2dt
дится к интегралу от рациональной функции: ∫R				2t	,	1 −t		2dt	.
дится к интегралу от рациональной функции: ∫R			1	2	,		2	2	.
			1	+ t	1 + t			1 + t
n
∑ f (ξi )	xi – интегральная сумма для функции f (x) на [a; b]
i =1
(рис. 5).
b		n
∫ f (x) dx = maxlimx → 0 ∑ f (ξi ) xi – определенный интеграл, где
a	i	i = 1
a		i = 1

предел не зависит от способа разбиения отрезка [a; b] и от способа выбора точек ξi xi , xi = xi − xi − 1.

y = f (x)

f (ξi )

				х
О a = x0 x1	x2	xi −1 ξi	xi	b = xn
	Рис. 5

Если существует конечный предел интегральной суммы, то функция y = f (x) называется интегрируемой на [a; b].

Если функция y = f (x) интегрируема на [a; b], то она огра-

ничена на этом отрезке.

Из ограниченности функции на отрезке не следует ее интегрируемость на этом отрезке. Например, функция Дирихле

1, если х − рациональное число
f (x) =	− иррациональное число
0, если х

ограничена на отрезке, но не интегрируема.

Свойства определенного интеграла:
∫b	f (x) dx = −∫a			f (x) dx,		∫a	f (x) dx = 0,	∫b	f (x) dx = ∫b		f (t) dt,
a			b			a		a		a
∫b ( f (x) ± g(x)) dx = ∫b					f (x) dx ± ∫b g(x) dx,
a				a			a
∫b cf (x) dx = c∫b				f (x) dx,		∫b	f (x) dx = ∫c	f (x) dx + ∫b		f (x) dx,
a			a			a	a		c
x			′			f (x) C0 [a;b] .
	∫ f (t) dt		= f (x) , где			f (x) C0 [a;b] .
a		x
							25

Пусть F(x) – первообразная для f (x) , тогда:
∫b	f (x) dx = F(b) − F(a) – формула Ньютона – Лейбница.
a
Если функция f (x)				имеет первообразную на отрезке [−a; a]		и
является четной, то ∫a		f (x) dx = 2∫a			f (x) dx.
	−a			0
Если функция f (x)				имеет первообразную на отрезке [−a; a]		и
является нечетной, то ∫a			f (x) dx = 0 .
		−a
Если функция f (x)				имеет период Т и на отрезке [0; T ] суще-

ствует первообразная для f (x), то для любого а справедливо равен-

ство a∫+T		f (x) dx = T∫ f (x) dx.
	a		0
	Пусть		x = ϕ(t) C1[α; β],			ϕ(α) = a,ϕ(β) = b,				f (x) C0 [a; b],
тогда	b		β		′	– замена переменной в определен-
					′
	∫ f (x)dx =∫ f (ϕ(t))ϕ (t) dt
	a		α
ном интеграле.
	∫b u dv = uv			ba − ∫b v du, где u(x), v(x) C1[a; b]						– интегрирование
	∫b u dv = uv			ba − ∫b v du, где u(x), v(x) C1[a; b]						– интегрирование
	a			a
по частям.
	Оценки для определенного интеграла:
	Если		f (x) ≥ 0 на отрезке [a; b] , то ∫b					f (x) dx ≥ 0.
							a
	Если		f (x) ≥ g(x)		на отрезке [a; b] , то ∫b				f (x) dx ≥ ∫b g(x) dx.
								a		a
	Если М – наибольшее, m – наименьшее значение функции
f (x)	на отрезке [a; b],				то m(b − a) ≤ ∫b		f (x) dx ≤ M (b − a).
						a
	∫b	f (x) dx = f (c)			(b − a) , c [a; b] , f (x) C0 [a; b] – теорема о
	a
среднем.
						26

fср =

∫b

f (x) dx

– среднее значение функции f (x)

на отрезке

b − a

[a; b].

∫b

f (x) dx

≤ ∫b

f (x)

dx.

а) Вычисление площади фигуры:

Площадь криволинейной трапеции, ограниченной сверху графиком функции y = f (x) ( f (x) ≥ 0 ), слева и справа соответ-

ственно прямыми x = a и x = b, снизу – отрезком [a; b] оси Ox

(рис. 6) вычисляется по формуле S = ∫b f (x) dx.

Если криволинейная трапеция, ограничена сверху кривой, заданной параметрическими уравнения-

ми x = x(t), y = y(t), y(t) ≥ 0, t [t1; t2 ], слева и справа

соответственно		прямыми
x = a и	x = b ,	снизу –	от-
резком	[a; b]	оси Ox,	то

ее площадь вычисляется по

формуле S = ∫y(t)x′(t) dt,

y = f (x)

О a

Рис. 6

где t1 , t2 определяются из равенств a = x(t1 ), b = x(t2 ).

Если y = f1 (x) и y = f2 (x) непрерывные функции на [a; b] и выполняется условие f2 (x) ≥ f1 (x) для любого x [a; b] (рис. 7), то площадь фигуры, заключенной между линиями, вычисляется по формулеS = ∫b ( f2 (x) − f1 (x)) dx.

Площадь криволинейного сектора (рис. 8), ограниченного линией, заданной в полярных координатах уравнением r = r(ϕ)

и двумя лучами

S = 1 ∫β r2 (ϕ) dϕ. 2 α

y = f1 (x)

О a

ϕ = α и ϕ = β , α < β, вычисляется по формуле

y = f2 (x)

			r = r (φ)
		β
	х	α	ρ
	х	О
b		О
b

Рис. 7 Рис. 8

б) Вычисление длины кривой:

Если линия задана на плоскости уравнением y = f (x) или

x = ϕ( y), то длина l дуги линии между точками			A(a; c),	B(b; d)
b		d
вычисляется по формуле l = ∫	′ 2	dx или l = ∫	′ 2	dy.
вычисляется по формуле l = ∫	1 + ( y )	dx или l = ∫	1 + (x )	dy.
a		c
Если линия задана параметрическими уравнениями				x = x(t),

y = y(t), то длина l дуги линии между точками M1 (t1 ), M2 (t2 ) вы-

числяется по формуле l = ∫ (x′)2 + ( y′)2 dt.

Если линия задана уравнением r = r(ϕ) в полярных координатах, то длина l дуги линии между точками M1 (ϕ1 ), M2 (ϕ2 ) вычис-

ϕ2
ляется по формуле l = ∫	r	2	′	2	dϕ.
ляется по формуле l = ∫	r		+ (r )		dϕ.
ϕ1

в) Вычисление объемов и площадей поверхностей:

Объем тела вращения, полученного при повороте криволинейной трапеции (ограниченной графиком функции y = f (x),

прямыми x = a, x = b и осью

V = π∫b f 2 (x) dx.

г) Площадь поверхности вращения, полученной при вращении криволинейной линии, заданной уравнением y = f (x) на отрезке

[a; b], вокруг оси Ox, равна

P = 2π∫b	f (x) 1+ f ′2 (x) dx.
a

ox ) вокруг оси Ox (рис. 9), равен

y = f (x)

О a

b х

Если известна пло-		Рис. 9
щадь поперечного	сечения

S(x) (рис. 10) тела	плоскостью, как функция от произвольной точки

x [a; b], тогда объем тела равен V = ∫b S(x) dx (вычисление объема

тела по известным площадям поперечных сечений).

S(a) S(x)

S(b)

b х

Рис. 10

Таблица приложений определенного интеграла

y = f (x)

r = r(ϕ)

x = x(t), y = y(t)

S ∫ f (x)dx

∫r2 (ϕ)dϕ

∫2

y(t)x′(t) dt

ϕ2

′

∫

(r′)

dϕ

∫

(x′)

+ ( y′)

∫ 1 + ( f )

ϕ1

2π

π∫ f 2 (x)dx

∫r3 sin ϕdϕ

π∫2

y2 (t)x′(t) dt

′ 2

′

2πy∫y(t)

′

2π f (x) 1+( f ) (x)dx

∫

2π∫rsinϕ r +(rϕ) dϕ

(x )

+(y ) dt

Физические приложения определенного интеграла:

Путь, пройденный телом, перемещаемым со скоростью

v = v(t) за промежуток времени [t1; t2 ] равен S = ∫v(t) dt.

Работа переменной силы, заданной функцией F = F(x) и на-

правленной вдоль оси Ox на отрезке [a; b] , равна A = ∫b F(x) dx.

Несобственные интегралы:

а) Несобственные интегралы первого рода (интегралы с бес-

конечными пределами):

+∞∫ f (x) dx = Rlim→ +∞	∫R	f (x) dx.
a	a

Если предел lim ∫ f (x) dx существует и конечен, то несоб-

R→ +∞ a

ственный интеграл +∞∫ f (x) dx называется сходящимся, а значение

этого предела – значением несобственного интеграла. Если предел не существует, то несобственный интеграл называется расходя-

щимся:

∫b	f (x) dx = Rlim→ −∞		∫b	f (x) dx,
−∞			R
+∞∫	f (x) dx = ∫a	f (x) dx + +∞∫ f (x) dx, где a – произвольная точка.
−∞	−∞			a

Признак сравнения несобственных интегралов. Если функции f (x) и g(x) непрерывны на промежутке [a; + ∞) и удовлетворяют

на нем условию 0 ≤ f (x) ≤ g(x), то из сходимости интеграла +∞∫ g(x) dx следует сходимость интеграла +∞∫ f (x) dx, а из расходимо-

сти интеграла +∞∫ f (x) dx следует расходимость интеграла +∞∫ g(x) dx.

б) Несобственные интегралы второго рода (интегралы от не-

ограниченных функций):

Пусть функция

y = f (x)

определена на промежутке [a; b) и

b −ε

lim f (x) = ∞ , тогда

∫

f (x) dx = lim

∫

f (x) dx.

x → b −

ε→ 0

Аналогично:

∫

f (x) dx = lim

∫

f (x) dx ,

если

lim f (x) = ∞,

ε→ 0 +

x → a +

a +ε

c−ε

∫

f (x) dx = lim

f (x) dx + lim

∫

f (x) dx, еслиa < c < b и lim f (c) = ∞.

ε→0+ ∫

η→0+

x → c

c+η

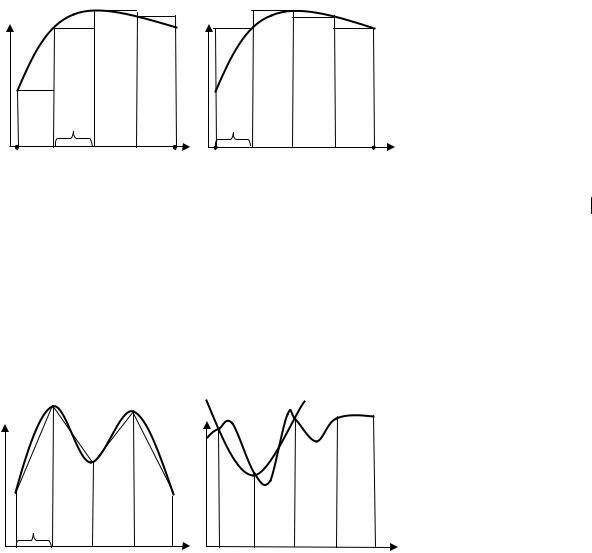
Приближенное вычисление определенных интегралов

∫b

f (x) dx ≈ h

( y0 + y1 + y2 +... + yn −1 )

– формула левых прямо-

угольников (рис. 11),

∫b

f (x) dx ≈ h

( y1 + y2 +... + yn )

– формула правых многоуголь-

ников (рис. 12), где h =

b − a

= a

+ kh, y

f (x ),

k = 0,1, 2, ..., n.

y = f (x)

yn−1

a = x0 x

b = xn

a = x

n −1

n −1 b = xn

Рис. 11

Рис. 12

Абсолютная погрешность метода прямоугольников определя-

ется неравенством:

(b − a)2 M

′

Rn ( f )

≤

где M = max

f (x)

a ≤ x ≤b

∫ f (x) dx ≈ h

+ y1 + y2

+ ... + yn − 1

–

формула трапе-

ций (рис. 13), где h =

b − a

, x = a + kh,

= f (x

k = 0,1, 2, ..., n.

y = f (x)

yn−1

y2n

y2n −1

a = x0 x1

xn −1

b = xn

a = x0 x1

x2n −1 b = x2n

Рис. 13

Рис. 14

Абсолютная погрешность метода трапеций определяется неравенством:

R ( f )

≤

(b − a)3 M

, где M = max

′′

f (x)

∫b

12n2

a ≤ x ≤ b

f (x) dx ≈

( y0 + 4( y1 + y3 +... + y2n − 1 ) + 2( y2 + y4 +... + y2n − 2 ) + y2n )

–

формула

парабол

(метод

Симпсона)

(рис. 14), где

h =

b − a

= a + kh,

yk = f (xk ), k = 0, 1, 2, ... , 2n.

Абсолютная погрешность метода трапеций определяется неравенством:

R ( f )	≤	(b − a)5 M	, где	M = max	f (IV) (x)	.



n		180(2n)4		a ≤ x ≤ b

VII. Решение задач с функцией от нескольких переменных

Пример 1. С помощью дифференциала приближенно вычис-


лить	0,98			.
лить		1, 01 0,97		.
	Решение.				Данное	число есть частное	значение	функции
f (x, y, z) =			x		при	значениях переменных	x = 0,98,	y =1,01,
f (x, y, z) =			y z		при	значениях переменных	x = 0,98,	y =1,01,
			y z

z = 0,97. Близкими значениями переменных к этим значениям явля-

ются x0

=1,

y0 =1,

=1,

для которых значение функции легко вы-

числяется

f (1,1,1) =1.

Тогда

x = x − x0 = −0,02,

y = y − y0

= 0,01,

z = z − z0

= −0,03.

Найдем дифференциал в общем виде:

df = fx′ x + fy′ y + fz′ z

или

df =

x +

y +

−

z y

y z

или

df =

x −

y −

xyz

y3 z

yz3

Вычислим

численное

значение

дифференциала

точке

df (x , y , z

) = −

0,02

−

0,01

0,03

= −0,01 − 0,005 + 0,015 = 0,00.

z0 ) + df ′(x0 ,

Подставляя в формулу

f (x,

z) ≈ f (x0 , y0 ,

y0 , z0 ),

получим:

0,98

≈1 − 0,00 =1, 00.

1,01 0,97

Замечание. На инженерном калькуляторе, имеющем 8 деся-

тичных разрядов, получаем значение

0,98

≈1, 00013096 , что

1,01 0,97

показывает достаточно хорошее приближение с помощью дифференциала.

Пример 2. Найти второй дифференциал d 2u функции
	y
u = f xy,		.

	x

Решение. Обозначим

z = xy,

t =

тогда получаем сложную

функцию u =

f (z, t),

где z = xy, t =

Найдем производные:

′

= y,

′

= x,

′′

=1,

′′

= 0.

zxx

zxy

zyy

′

′′

2 y

′′

= 0.

= x

= − x2

= − x2 , ty

, txx =

, txy

, tyy

Имеем:

du =

′

где

′

= ydx + xdy,

fz dz

+ ft dt,

dz = zx dx

+ zy dy

dt = tx′dx + t′y dy = −

dx +

dy.

Найдем дифференциал от первого дифференциала:

′

u = d( fz )dz + fz d(dz) + d( ft

)dt

+ ft d(dt) =

′′

′

′′

′

( fzz dz + fzt dt)dz + fz d

+ ( ftt dz

+ ftt dt)dt + ft d

′′

(dz)

′′

′

где

u = fzz

2 fzt dzdt + ftt

(dt)

+ fz d

+ ft d

′′

(dx)

′′

= 2dxdy,

так как

z = zxx

2zxy dxdy + zyy dy

d(dx) = 0, d(dy) = 0,

′′

(dx)

′′

2 y

(dx)

dxdy.

− x2

t = txx

2txy dxdy + tyy dy

Подставляя значения dz, dt, d 2 z, d 2t, получим:

u = fzz′′( ydx + xdy)

+ 2 fzt′′( ydx + xdy) −

dx +

2 y

+ ftt′′

−

dx +

+ fz′ 2dxdy

+ ft

′

(dx)

−

dxdy

′′

′′ 2

′

d 2u =

fzz′′y2 − 2

fzt y

ftt

+ 2

ft y

dx2

fzz′′xy −

ftt′′

fz′−

f ′

fzz′′x2 + 2 fzt′′

′′

+ 2

dxdy

dy2 .

Пример 3. Найти производную функции

z = ln (2x2 + y2 )

точке M (1; −1)

по направлению к точке N(−2; −5).

Решение.

Имеем

= l = (−3;−4),

= 5,

cos α = −

2 y

cosβ = −

zx′

z′y =

, zx′(M ) =

zx′(M ) = −

2x2 + y2

Подставляя в формулу

дz

сosα +

дz

cosβ, получим:

дl

дx

дy

дz

−

= −

дl

Отрицательный знак производной означает, что функция убывает в этом направлении.

Пример 4. Найти экстремум функции z = x3 + y3 −18xy. Решение. Найдем частные производные первого порядка: zx′ = 3x2 −18y, z′y = 3y2 −18x.

Используя			необходимое условие экстремума zx′ = 0, z′y = 0,
находим стационарные точки:
	2	− 6 y = 0,
x
		− 6x =	0.
y2

Следовательно, x1 = 0, y1 = 0, x2 = 6, y2 = 6.

Получаем две точки A(0; 0) и B(6; 6) возможного экстремума.

Найдем частные производные второго порядка: zxx′′ = 6x, z′′yy = 6 y, z′′xy = −18.

Вычислим значения частных производных второго порядка в стационарных точках:

а) zxx′′ (A) = 0, z′′yy (A) = 0, z′′xy (A) = 0.

Достаточный признак в этом случае не дает ответа. Требуется дальнейшее исследование данной функции.

При y = 0 получаем z = x3 . Плоскость y = 0 пересекает график функции z = x3 + y3 −18xy по кубической параболе z = x3 . При

x = 0 кубическая парабола не имеет экстремума, а поэтому и данная функция в точке (0; 0) тем более не имеет экстремума.

б) zxx′′ (B) = 36, z′′yy (B) = 36, zxy′′ (B) = −18.

Составим дискриминант Δ=z′′xx (B) z′′yy (B) −z′′xy2 (B) =36 36−182 >0, причем zxx′′ (B) > 0, следовательно, в точке В функция достигает экстремум. Локальный минимум функции равен zмин = −216.

VIII. Применение производной функции нескольких переменных

Пример 5. Из всех треугольников, вписанных в окружность, найти тот, площадь которого наибольшая.

		Решение. Пусть	АВС – произвольный треугольник (рис. 15),
вписанный в окружность радиуса R. Площадь треугольника равна
S =	1	bcsin α.	С
S =	2	bcsin α.	С
	2

Из теоремы синусов sinaα =

= sinb β = sinc γ = 2R выразим сторо-

ны b = 2R sin β, c = 2R sin γ и, под-

ставляя их в выражение площади,

	γ	a
b		R

αβ

Аc В

получим	S = 2R2 sin αsin βsin γ,
где R −const.		Рис. 15

Получили функцию от трех переменных α, β, γ, причем переменные связанны условием

α +β + γ = π.

Углы треугольника удовлетворяют условиям 0 < α < π, 0 < β < π, 0 < γ < π, α +β + γ = π.

Область определения функции изображена на рис. 16.

Первый способ решения задачи.

Выразим γ через остальные углы и перейдем к функции от двух независимых аргументов α, β.

γ = π − (α +β), S = 2R2 sin αsin βsin (α +β), где переменные удовлетворяют условиям: α > 0, β > 0, α +β < π. Область определения функции S = S(α, β) изображена на рис. 17.

Найдем производные функции S = S(α, β) :

Sα′ = 2R2 sin β(cos αsin (α +β) + sin αcos(α +β)) = 2sinβsin(2α +β), Sβ′ = 2R2 sin α(cosβsin (α +β) + sin βcos(α +β)) = 2sin αsin(2β + α).

Найдем значения переменных, для которых Sα′ = 0, Sβ′ = 0 :

sin βsin

(2α +β) = 0,

2α +β = kπ,

где k N, n N,

sin αsin

(2β + α) = 0,

2β+ α = nπ,

α = (2k − n) π, β = (2n − k)

π.

π β

Рис. 16

Рис. 17

Числа

2k − n и 2n − k

являются целыми,

следовательно,

ве-

личины α и β кратны углу

π.

В области определения существует

π, поэтому α =

π, β =

π, γ =

π.

единственная пара чисел, кратных

Докажем, что для этих значений функция достигает макси-

мального значения в точке A

′′

sin βcos(2α +β),

′′

Sαα =

Sαα (A) = −2

′′

sin αcos(2β + α),

′′

Sββ = 4R

Sββ (A) = −2

′′

′′ 2

> 0.

Sαβ = 2R

sin 2(α +β), Sαβ (A) = − 3R

SααSββ − Sαβ

Следовательно, равносторонний треугольник среди всех треугольников, вписанных в окружность, имеет наибольшую площадь.

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.09.201976.8 Кб0Документация_25кадр.doc
#
16.12.2018736.77 Кб132Долгих 2002 - Патофизиология обмена веществ.doc
#
13.05.2015202.75 Кб47ДОМАШНЯЯ РАБОТА_1_14_БЭ.doc
#
22.11.2019411.14 Кб6доработка 5.doc
#
13.05.2015109.03 Кб21Древности Сибири.pdf
#
13.05.2015693.69 Кб17Дубовик О.А., Совертков П.И.pdf
#
13.05.2015918.02 Кб34Задание №2-2.doc
#
13.05.2015983.55 Кб13Задание №2-3.doc
#
13.05.2015434.18 Кб9Задание №2-5 (дисперс. анализ_регрессия).doc
#
13.05.2015173.06 Кб6Задание2 семетр исправл.doc
#
09.11.201990.62 Кб6задания для самостоятельной работы.doc