
Елементи теорії графів. Для 1к
.pdf
35
Ланцюги, цикли, шляхи та контури графа
Ланцюги та цикли – для неографа, шляхи й контури – для орграфа.
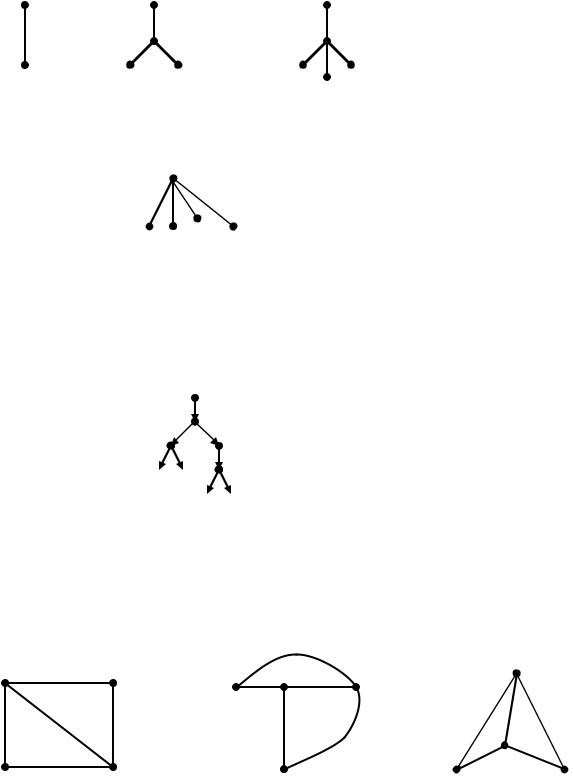
Ланцюг – скінченна послідовність ребер, де кінець одного ребра суміщений з початком іншого.
1) |
g1 |
|
g2 |
g3 |
|
Ланцюг < g1, g2, g3 > |
|
X1 |
X2 |
|
X 3 |
X 4 |
|
2) |
g1 |
g2 |
g3 |
g4 |
Ланцюг < g1, g2, g3, g4, g5 > |
|
|
X 1 |
X2 |
g5 |
X 3 |
X 4 |
|
|
X 4 |
|
|
X 5 |
|
|
3) |
g1 |
|
|
g2 |
|
Ланцюг < g1, g2, g2, g3 > |
|
X 1 |
|
X2 |
|
X3 |
|
|
X 4 |
g3 |
|
|
|
|
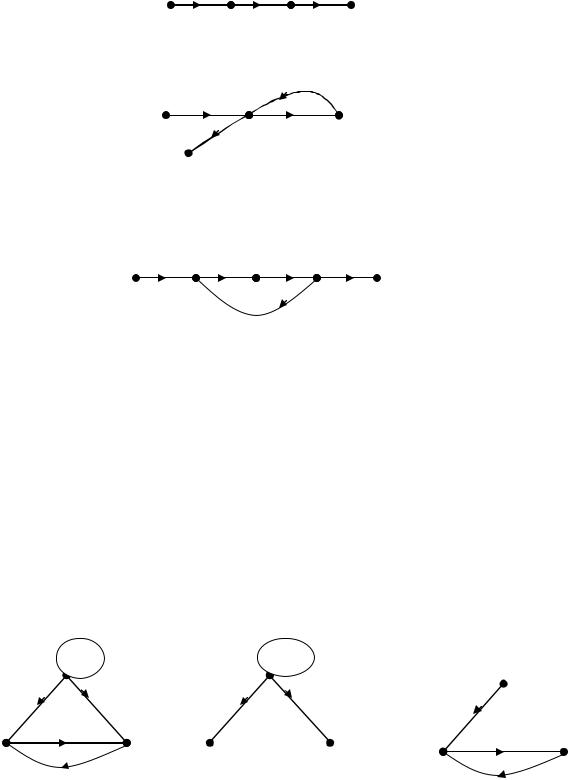
Ланцюг: елементарний – немає повторення ні вершин, ні ребер [ 1) ]
простий – допускається повторення вершин [ 2) ]
складний – допускається повторення вершин і ребер [ 3) ]
Цикл – скінченний ланцюг, що починається і закінчується в одній і тій же вершині.
|
X 1 X 2 |
X 1 X 2 X 3 |
X1 X 2 X 3 |
X 3 |
|
|
X 4 |
X 4 |
Елементарний |
Простий цикл |
Складний цикл |
цикл |
|
|
36
Орграф
Шлях – шлях для орграфа.
1. |
(елементарний шлях) |
g1 |
g2 |
g3 |
< g1, g2, g3 > - 3 дуги |
|
|
|
X 1 |
X 2 |
X 3 |
X 4 |
|
2. |
(простий шлях) |
|
g1 |
g2 |
g3 |
< g1, g2, g3, g4 > - 4 дуги |
|
|
X 1 |
X 2 |
|
X 3 |
|
|
|
g4 |
|
|
|
|
3. |
(складний шлях) |
g1 |
g2 |
g3 |
g4 |
|
|
X 1 |
X 2 |
X 3 |
X 4 |
X 5 |
|
|
|
|
g5 |
|
|
|
< g1, g2, g3, g5, g2, g3, g4 > - 7 дуг
Контур – поняття для орграфа (аналогічне циклу неографа).
Довжина шляху – кількість дуг, що складають цей шлях.
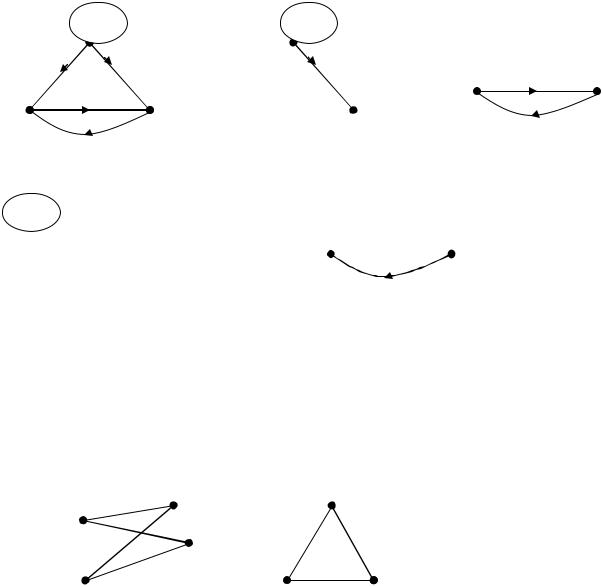
Частковий граф, підграф, частковий підграф.
Частковий граф (суграф) H графа G отримуємо з графа G викреслюванням тільки ребер (дуг)
|
Х1 |
|
X 1 |
|
X 1 |
|
|
|
|
|
|
G |
→ |
H1 |
или |
H2 |
|
X 2 |
X 3 |
X 2 |
X 3 |
X 2 |
X 3 |
37
Підграф G1 графа G утворюється з G видаленням деяких вершин та
інцидентних їм ребер (дуг) |
|
|
|
||
|
X 1 |
|
X 1 |
|
|
G |
|
→ |
G1 |
або |
G 2 |
X 2 |
X 3 |
|
X 3 |
Х2 |
Х3 |
Частковий підграф Gij |
утворюється з підграфа Gi видаленням деяких ребер |
||||
X 1 |
● |
|
|
|
|
|
|
|
|
|
|
|
|
|
Х2 |
Х3 |
|
G11 |
|
|
G21 |
|
|
●
Х3
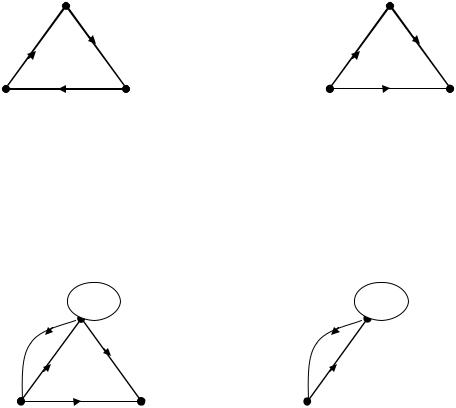
Зв’язність графа
У неографі
Дві вершини Хi та Хj зв’язані, якщо існує ланцюг з кінцями у вершинах Хi та Хj.
|
|
X2 |
X6 |
|
Х1 |
и Х3 – зв’язані |
|
X1 |
G2 |
|
|
Х1 |
и Х5 - не зв’язані |
G |
G1 |
X3 |
|
|
|
|
|
X4 |
X5 |
|
X7 |
|
|
|
|
|
|
|
|
|
Неограф зв’язний, якщо будь-які дві його вершини зв'язані. G – незв’язний, G1 –
зв’язний.
Компонента зв’язності неографа – підграф, що задовольняє умові зв’язності та максимальності.
Умова максимальності – додавання у підграф хоча б однієї вершини порушує його зв’язність. G1 и G2 – компоненти зв’язності графа.
Висновки:
38
1.Зв’язний неограф має одну компоненту зв’язності, якою він і є.
2.Незв’язний неограф складається з компонент зв’язності.
Орграф
1) Орграф називається сильно зв’язним, якщо для будь-якої пари вершин xi , xj
існують шляхи з xi → xj та xj → xi.
2) Орграф називається не сильно зв’язним, якщо для <xi , xj> існує або xi → xj, або xj → xi.
Сильно зв’язний |
Не сильно зв’язний |
Х2 |
Х2 |
Х1 Х3 Х1 Х3
Орграф, що не задовольняє умові 1), називається незв’язним.
Компонентою сильної зв’язності орграфа G називається такий його підграф, який задовольняє умовам сильної зв’язності та максимальності.
Х2 |
Х2 |
G |
|
G1 |
- компонента сильної |
X1 |
X3 |
X1 |
зв'язності |
Висновки:
1. Сильно зв'язний орієнтований граф сам є компонентою сильної зв'язності.

39
2. Не сильно зв'язний орієнтований граф може мати декілька компонент сильної
зв'язності.
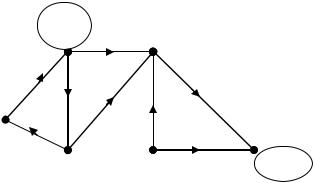
Метод розкладання орієнтованого графа на компоненти сильної зв'язності.
Базується на визначенні прямого та оберненого транзитивних замикань для вершин графа.
Транзитивне замикання вершини хi (позначається xi ) – множина вершин,
включаючи і вершину хi, до яких існують шляхи, що починаються в хi.
xi {xi } 1xi 2 xi 3 xi 
хi |
|
|
хi |
|
σ¹хi |
σ²хi |
σ³хi |
σ‾¹хi |
σ‾²хi σ‾³хi |
Обернене транзитивне замикання хi – множина вершин, включаючи хi, з яких можна різними шляхами потрапити до хi.
Компонента сильної зв'язності: C(xi ) xi xi 1 (1)
Алгоритм розкладу орієнтованого графа на компоненти сильної зв'язності.
1.Для довільної вершини xi знайти xi .
2.Для цієї ж вершини знайти xi 1 .
3.Користуючись формулою (1) знайти С(хi).
4.Взяти довільну вершину xj xi и повторити для неї пункти 1-3.
5.Алгоритм виконувати, доки не вичерпаються усі вершини
На базі цього алгоритму побудуємо матричний алгоритм Мальгранжа-Томеску.
40
Алгоритм Мальгранжа-Томеску
1.Подати граф матрицею суміжності R.
2.Доповнити матрицю зліва стовпчиком xi и знизу рядком xi 1 .
3.Отримати за деяким алгоритмом xi , потім xi 1 .
4.Отримати компоненту сильної зв'язності за формулою C(xi ) xi xi 1 .
5.З матриці R викреслити строки та стовпці, що відповідають вершинам, що увійшли до С(хi).
6.Алгоритм продовжувати до тих пір, поки не будуть викреслені усі строки та стовпці матриці.
Алгоритм заповнення стовпця σ*хi та рядку σ*хi ‾ ¹
1. У комірці стовпця xi для вершини хi, що відповідає рядку хi матриці
суміжності R, поставити 0.
2.Якщо у матриці R на перетині рядка хi та стовпця хj, хk, хl,… , стоять одиниці, то в комірках стовпця xi , відповідних рядкам хj, хk, хl,… , поставити 1.
3.Якщо в матриці R на перетині строк хj, хk, хl,… , з стовпцями хp, хm,…, хq стоять 1,
то у комірках стовпця xi , відповідних рядкам хp, хm,…, хq матриці R поставити 2.
4. Процес заповнення комірок стовпця xi продовжується до використання усіх доступних рядків матриці.
5. Процес заповнення рядка xi 1 аналогічний алгоритму заповнення стовпця
xi , але розглядаються не рядки, а стовпці.
X2 X4
X1
X6
41
X3 X5
|
|
X1 |
X2 X3 X4 X5 |
X6 |
Σ*х |
1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X1 |
|
|
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X2 |
|
|
1 |
1 |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ*х |
|
|
|
|
|
|
R= |
X3 |
1 |
|
|
|
1 |
|
|
|
|
2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ*х |
|
|
|
X4 |
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
0 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ*х |
X5 |
|
|
|
|
|
1 |
|
|
1 |
|
X |
|
|
X |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X6 |
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
1 |
|
|
1 |
|
|
0 |
σ*х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
‾ ¹ |
0 |
2 |
1 |
|
X |
X |
X |
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ*х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
X |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
4 ‾ ¹ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
σ*х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
‾ ¹ |
|
|
0 |
X |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
σ*х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
‾ ¹ |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С(x1) = { x1, x2, x3, x4, x6 } ∩ { x1, x2, x3 } С(x1) = { x1, x2, x3 }
С(x4) = { x4, x6 } ∩ { x4, x5 } = { x4 } С(x5) = { x5, x6 } ∩ { x5 } = { x5 } С(x6) = { x6 }
42
Дерева та ліси
Дерево – скінченний зв'язний граф, що містить щонайменше 2 вершини та не містить циклів.
Ліс – незв'язний граф, кожна компонента зв'язності котрого є деревом.
Лагранжеве дерево – дерево, усі гілки якого мають спільну вершину.
Прадерево – орієнтований граф с коренем у вершині и такий, що в кожну вершину, окрім вершини Х1 , входить рівно одна дуга, а у вершину Х1 не входить жодна дуга.
Ізоморфізм
Два графа називаються ізоморфними, якщо вони можуть бути зображені
геометрично однаково з точністю до позначень або номерів вершин.
Х2 |
X3 |
|
|
Z1 |
|
Y1 |
Y2 |
Y3 |
|
|
|
|
|
Z3 |
Х1 |
Х4 |
У4 |
Z2 |
Z4 |
43
Цикломатичне число графа та його застосування
Нехай граф G = (Х, δ) має n вершин та m ребер.
Скелет (остов) графа – дерево, гілки якого (ребра графа) інцидентні усім вершинам графа.
Будь-який остов має (n-1) ребро.
Граф може містити декілька остовів:
G 2
|
|
|
|
4 |
5 |
|
1 |
|
3 |
(1) |
|
1 |
(2) |
|
|
|||||
|
|
|
|
2 |
6 |
|
4 |
|
|
7 |
3 |
|
|
5 |
|
6 |
|
|
8 |
|
Якщо до остову графа додати одне ребро, яке не входить в остов, то утвориться цикл з участю цього ребра.
Такий цикл називається фундаментальним циклом. Фундаментальні цикли – елементарні.
Приклад. Граф G має 6 вершин та 8 ребер. Остов (1) має 6 вершин та 5 ребер.
Остов (2) має n = 6 вершин та n-1 = 5 ребер. Ребра 1, 2, 3 не входять до остова.
Число фундаментальних циклів дорівнює числу ребер, які не належать до остова.
Це число називається цикломатичним числом і позначається υ(G), G m n 1.
Цикломатичне число дозволяє підрахувати усі можливі цикли графа.
Традиційно фундаментальні цикли позначаються Фi и представляються рядками спеціальної матриці, яку називають матрицею фундаментальних циклів. Для її побудови граф подаємо геометрично. Нумеруємо ребра графа, спочатку ті, що не увійшли до остову, потім ребра остову. Число стовпців матриці фундаментальних циклів дорівнює числу ребер графа, число строк дорівнює числу фундаментальних циклів (цикломатичному числу).

44
Приклад для остова (1):
|
1 |
2 |
3 |
4 |
|
5 |
|
6 |
7 |
8 |
|
|
|
|
|
|
|
|
|
|
|
Ф1 |
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф2 |
|
1 |
|
|
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф3 |
|
|
1 |
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
Ф1 Ф2 |
1 |
1 |
0 |
|
0 |
|
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
Ф1 Ф3 |
1 |
0 |
1 |
|
1 |
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
Ф1 Ф2 Ф3 |
1 |
1 |
1 |
|
0 |
|
0 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
Правило заповнення матриці:
На перетині рядка Фi та стовпця j ставиться 1, якщо ребро з індексом j належить фундаментальному циклу.
Будь-який цикл графу утворюється як лінійна комбінація (сума по модулю 2) векторів фундаментальних циклів. При цьому лінійна комбінація може утворювати структуру, що не є циклом.
Число усіх можливих циклів 2 (G) 1. (У прикладі (G) 3 , 23 1 7 ).
Розрізи у графах
1.Розріз графа модульної схеми на дане число підсхем.
2.Розріз на довільне число підсхем з приблизно рівним числом вершин у кожній підсхемі.
3.Область застосування
Розріз – це множина ребер, видалення яких з графа подає скінченний незв'язний граф, що складається щонайменше з 2-х компонент зв'язності. Розріз позначається
Ki.
|
Х2 |
|
Х5 |
|
|
5 |
6 |
3 |
|
Х1 |
1 |
|
8 |
K1 { x4 , x5 , x4 , x6 } |
4 2 Х4 7
Х3 Х6
