6.3. Сфера застосування двоїстого симплекс-методу

1. Розв’язок ЗЛП безпосередньо. Двоїстий симплекс-метод може безпосередньо застосовуватися для розв’язання тільки певного класу задач. У цих задачах знаки коефіцієнтів цільової функції та знаки обмежень не можуть бути довільними.

Значення коефіцієнтів цільової функції:

а) якщо цільова функція мінімізується, то всі коефіцієнти цільової функції повинні бути невід’ємними:  c_j  0;

б) якщо цільова функція максимізується, то всі коефіцієнти цільової функції мають бути недодатними:  c_j  0.

Знаки обмежень. Обмеження початкової ЗЛП з невід’ємними компонентами вектора b повинні мати лише знаки "" і "" (але не всі одночасно типу "").

2. Розв’язок ЗЛП у випадках, коли після одержання оптимального розв’язку в задачу вводиться нове (додаткове) обмеження (найбільш важлива сфера застосування).

Параметричне програмування – це метод визначення, яким чином зміниться розв’язок задачі: чи зміною вектора коефіцієнтів ЦФ, чи зміною вектора обмежень.

6.4. Приклад застосування двоїстого симплекс-методу

_{Приклад 6.1. Розв’яжемо ЗЛП двоїстим симплекс-методом:}

min z = x₁ + x₂; (6.8)

; (6.9)

; (6.10)

; (6.11)

. (6.12)

Зведемо спочатку всі обмеження до типу ””; для цього нерівності типу “” помножимо на –1:

;

;

.

А тепер у кожне з них введемо відповідну залишкову змінну:

;

;

.

Ітерація 1. Початковий базисний розв’язок (недопустимий) задачі такий:

=.

На рис. 6.1 цей розв’язок відповідає точці А (0, 0).

Заповнюємо симплекс-таблицю (табл. 6.2).

Таблиця 6.2

Базисні змінні	x1	x2	s1	s2	s3	Розв’язок
z	-1	-1	0	0	0	0
s1	-2	-1	1	0	0	-4
 s2	-1	-2	0	1	0	-4
s3	1	1	0	0	1	10

Значення залишкових змінних не забезпечують одержання допустимої стартової точки прямої задачі, але всі елементи z-рядка (d_j) є недодатними — умова оптимальної задачі на мінімізацію виконується.

Крок 1. Вибираємо змінну, що виводиться з множини базисних

За умовою допустимості за виводжувану з базису змінну вибирається най­більша за модулем від’ємна базисна змінна. Таких змінних дві: s₁ = –4; s₂ = –4. У цьому випадку можна вибрати будь-яку змінну. Виберемо змінну s₂.

Крок 2. Вибираємо змінну, що вводиться у множину базисних

За умовою оптимальності змінна, що вводиться у базис, вибирається з небазисних таким чином: обчислюються відношення коефіцієнтів лівої частини z-рів­няння до відповідних коефіцієнтів рівняння, яке відповідає виводжуваній змінній. Відношення з додатними або нульовими значеннями знаменника не враховуються. У задачі на мінімізацію змінній, що вводиться, повинне відповідати найменше з вказаних співвідношень (табл. 6.3). У задачі на максимізацію вибираємо відношення, найменше за абсолютною величиною:

Таблиця 6.3

Базисні змінні	x1	x2	s1	s2	s3	Розв’язок
Z	-1	-1	0	0	0	0
s2	-1	-2	0	1	0	-4
Відношення	1	1/2	—	—	—	—

Обчислюємо  = min{1,¹/₂} = ¹/₂, тобто вводимо до базису змінну x₂.

Крок 3. Виконаємо операцію заміщення, використовуючи перетворення Жордана-Гаусса (тобто звичайні симплекс-перетворення) (табл. 6.4).

Таблиця 6.4

Базисні змінні	x1	x2	s1	s2	s3	Розв’язок
z	-1/2	0	0	-1/2	0	2
s1	-3/2	0	1	-1/2	0	-2
x2	1/2	1	0	-1/2	0	2
s3	1	0	0	1/2	1	8

Новий базисний розв’язок відповідає точці В (2, 0) (рис. 6.1).

Ітерація 2

Крок 1. Вибираємо змінну, що виводиться з множини базисних.

Розв’язок ще не допустимий (s₁ = –2). За умовою допустимості за змінну, що виводиться з базису, вибираємо змінну s₁.

Крок 2. Вибираємо змінну, що вводиться до базису (табл. 6.5).

Таблиця 6.5

Базисні змінні	x1	x2	s1	s2	s3	Розв’язок
z	-1/2	0	0	-1/2	0	2
 s1	-3/2	0	1	-1/2	0	-2
x2	-1	1	0	-1/2	0	2
s3	1	0	0	1/2	1	8
Відношення	1/3	—	—	1	—

Обчислюємо  = min{¹/₃, 1} = ¹/₃, тобто вводимо до базису змінну x₁.

Крок 3.Виконуємо операцію заміщення (табл. 6.6).

Таблиця 6.6

Базисні змінні	x1	x2	s1	s2	s3	Розв’язок
z	0	0	-1/3	-1/3	0	8/3
x1	1	0	-2/3	1/3	0	4/3
x2	0	1	1/3	-2/3	0	4/3
s3	0	0	1/3	1/3	1	22/3

Розв’язок, що є оптимальним і допустимим, відповідає точці С(⁴/₃, ⁴/₃).

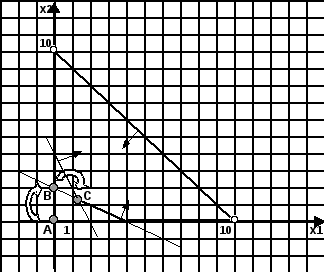
Рис. 6.1