
- •Поверхневі інтеграли теорія поля київ-2014
- •Передмова
- •І.Поверхневі інтеграли
- •Іi.Вступ до математичної теорії поля
- •1)Похідну цієї функції у точці у напрямі вектора;
- •2)Величину та напрям найбільшої зміни функції у точці .
- •6. Потік векторного поля. Дивергенція.
- •7. Циркуляція векторного поля. Ротор.
- •8. Потенціальне, соленоідальне і гармонічне векторні поля
- •Література
1)Похідну цієї функції у точці у напрямі вектора;
2)Величину та напрям найбільшої зміни функції у точці .
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
.
9.
![]() .
.
10.
![]() .
.
11.
![]() .
.
12.
![]() .
.
13.
![]() .
.
14.
![]() .
.
15.
![]() .
.
16.
![]() .
.
17.
![]() .
.
18.
![]() .
.
19.
![]() .
.
20.
![]() .
.
21.
![]() .
.
22.
![]() .
.
23.
![]() .
.
24.
![]() .
.
25.
![]() .
.
26.
![]() .
.
27.
![]() .
.
28.
![]() .
.
29.
![]() .
.
30.
![]() .
.
6. Потік векторного поля. Дивергенція.
Розглянемо спочатку гідродинамічну задачу, яка допоможе зрозуміти поняття потоку векторного поля через деяку поверхню.
1.Нехай
всередині деякого каналу тече потік
води із швидкістю
![]() .
У цьому потоці перпендикулярно до
вектора
.
У цьому потоці перпендикулярно до
вектора![]() установлена плоска пластина з площею
установлена плоска пластина з площею![]() ,
через яку протікає вода (наприклад,
фільтр).
Потоком
,
через яку протікає вода (наприклад,
фільтр).
Потоком
![]() вектора
вектора![]() через пластину з площею
через пластину з площею![]() назвемо об’єм води, що протікає через
цю пластину за одиницю часу. Оскільки
всі частинки рідини рухаються з постійною
швидкістю, то за одиницю часу вони
перемістяться на відстань
назвемо об’єм води, що протікає через
цю пластину за одиницю часу. Оскільки
всі частинки рідини рухаються з постійною
швидкістю, то за одиницю часу вони
перемістяться на відстань
![]() .
Об’єм рідини, що пройде через
.
Об’єм рідини, що пройде через
![]() дорівнює об’єму циліндра з основою
дорівнює об’єму циліндра з основою![]() і висотою
і висотою![]() :
:![]() .
Отже у даному випадку потік
.
Отже у даному випадку потік![]() .
.
2.
Нехай тепер у тому ж каналі пластину
площею
![]() установлено не перпендикулярно до руху
води, а під деяким кутом
установлено не перпендикулярно до руху
води, а під деяким кутом![]() . Тоді об’єм рідини, що пройде через
пластину з площею
. Тоді об’єм рідини, що пройде через
пластину з площею![]() ,
дорівнює об’єму похилого циліндра з
площею основи
,
дорівнює об’єму похилого циліндра з
площею основи![]() і висотою
і висотою![]() і при цьому потік
і при цьому потік![]() .
.
3.
Нехай тепер буде не рівна пластина, а
деяка орієнтована поверхня
![]() .
Розділимо поверхню
.
Розділимо поверхню![]() на маленькі частинки
на маленькі частинки![]() ,
,![]() ,
площі яких позначимо
,
площі яких позначимо![]() .
Сумарний потік
.
Сумарний потік![]() через поверхню
через поверхню![]() приблизно буде дорівнювати
приблизно буде дорівнювати![]() .
Рівність буде тим точнішою, чим дрібніший
буде поділ поверхні
.
Рівність буде тим точнішою, чим дрібніший
буде поділ поверхні![]() на частинки
на частинки![]() .
Таким чином, приходимо до поверхневого
інтегралу.
.
Таким чином, приходимо до поверхневого
інтегралу.
Означення.
Потоком
![]() векторного
поля
векторного
поля
![]()
через
задану поверхню
![]() в напрямку нормалі
в напрямку нормалі![]() називається поверхневий інтеграл
називається поверхневий інтеграл
 (6.1)
(6.1)
Приклад
1.Обчислити
потік векторного поля
![]() через
верхню частину площини
через
верхню частину площини
![]() ,
розміщену в першому октанті.
,
розміщену в першому октанті.
Потік
через поверхню
![]() знаходимо за формулою (6.1), маємо
знаходимо за формулою (6.1), маємо
![]() (6.2)
(6.2)
Ортогональний
вектор до площини
![]() записується в наступному вигляді
записується в наступному вигляді
![]() .
.
![]() .
Оскільки
.
Оскільки
![]() ,
то це і вказує на верхню частину площини.
Таким чином, поверхневий інтеграл
другого роду
(6.2) зв’язаний з поверхневим інтегралом
першого роду:
,
то це і вказує на верхню частину площини.
Таким чином, поверхневий інтеграл
другого роду
(6.2) зв’язаний з поверхневим інтегралом
першого роду:
![]() .
(6.3)
.
(6.3)
Оскільки
рівняння площини
![]() ,
то елемент площі
,
то елемент площі
![]()
і інтеграл (6.3) зводиться до подвійного
 .
.
Приклад
2.Обчислити
потік векторного поля
![]() через
зовнішню частину сфери
через
зовнішню частину сфери
![]() ,
розміщену в першому октанті.
,
розміщену в першому октанті.
Потік векторного поля через поверхню записуємо по формулі (6.1)
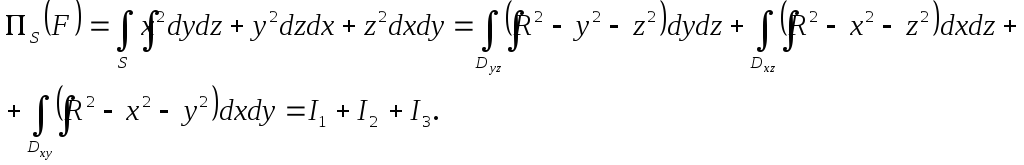
Проекціями
даної частини сфери на координатні
площини
![]() є одинакові четвертини кругів радіуса
є одинакові четвертини кругів радіуса![]() і підінтегральні функції одинакові,
тому
і підінтегральні функції одинакові,
тому![]() .
.

Приклад
3.Знайти
потік векторного поля
![]() через
повну зовнішню поверхню циліндра радіуса
через
повну зовнішню поверхню циліндра радіуса
![]() і висотою
і висотою![]() ,
якщо початок координат знаходиться у
центрі нижньої основи циліндра, а вісь
циліндра збігається з віссю
,
якщо початок координат знаходиться у
центрі нижньої основи циліндра, а вісь
циліндра збігається з віссю![]() .
.
Повна
поверхня
![]() складається з бічної поверхні
складається з бічної поверхні![]() ,
нижньої основи
,
нижньої основи![]() ,
та верхньої основи
,
та верхньої основи![]() .
Тому
.
Тому![]() .
.
Рівняння
бічної поверхня циліндра
![]() .
Звідси вектор нормалі до цієї поверхні
.
Звідси вектор нормалі до цієї поверхні![]() ,
а тому направляючі косинуси
,
а тому направляючі косинуси
![]() ,
,
![]() ,
,
![]() ,
оскільки рівняння нижньої основи
,
оскільки рівняння нижньої основи
![]() ,
то
,
то
![]() .
Накінець отримуємо
.
Накінець отримуємо
![]() ,
,
![]() .
.
Нехай
замкнена поверхня
![]() обмежує деяку область
обмежує деяку область![]() в
в![]() .
Розглянемо поле швидкостей
.
Розглянемо поле швидкостей![]() протіканння рідини,
протіканння рідини,![]() -
потік через цю поверхню. Якщо
-
потік через цю поверхню. Якщо
![]() ,
то це означає, що із
,
то це означає, що із
![]() виливається більше рідини, чим вливається.
В цьому випадку говорять, що всередині
виливається більше рідини, чим вливається.
В цьому випадку говорять, що всередині![]() є джерела, які поповнюють потік рідини.
Якщо ж
є джерела, які поповнюють потік рідини.
Якщо ж![]() ,
то це означає, що в
,
то це означає, що в![]() є стоки, які поглинають рідину з потоку.
Отже, величина потоку
є стоки, які поглинають рідину з потоку.
Отже, величина потоку![]() характеризує продуктивність джерел
(стоків), що знаходяться в області
характеризує продуктивність джерел
(стоків), що знаходяться в області![]() ,
її ще називають продуктивністю області.
,
її ще називають продуктивністю області.
Аналогічно,
потік довільного внкторного поля
![]() через замкнену поверхню
через замкнену поверхню![]() називаютьпродуктивністю
області
називаютьпродуктивністю
області
![]() ,
яка обмежена цією поверхнею. Якщо
позначити через
,
яка обмежена цією поверхнею. Якщо
позначити через![]() об’єм області
об’єм області![]() ,
то відношення
,
то відношення
![]() (6.4)
(6.4)
є
середньою продуктивністю джерел (стоків)
поля
![]() всередині області
всередині області![]() .
.
Якщо
область
![]() зменшуючись стягується в точку
зменшуючись стягується в точку![]() ,
то таку границю прийнято називатидивергенцією
векторного поля
,
то таку границю прийнято називатидивергенцією
векторного поля
![]() в точці
в точці![]() .
.
Отже за означенням
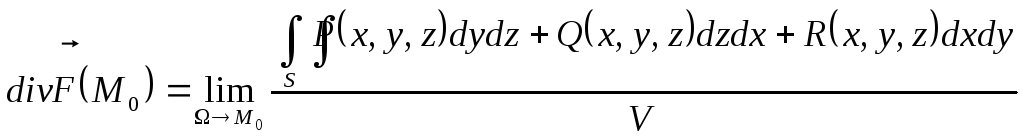 .
(6.5)
.
(6.5)
Використовуючи формулу Гауса-Острогорадського, фомулу (6.5) спростимо.

де
![]() -
деяка точка всередині області
-
деяка точка всередині області![]() .
Якщо область
.
Якщо область![]() стягується в точку
стягується в точку![]() ,
то
,
то![]() .
Звідси випливає:
.
Звідси випливає:
Якщо задане векторне поле
![]() ,
,
то його дівіргенція
![]() .
(6.6)
.
(6.6)
Зауваження. Формулу Гауса-Остроградського (3.1) можна коротко записати, використовуючи рівність (6.6):
 ,
,
![]() ,
,
![]() -
вектор ортогональний до поверхні
-
вектор ортогональний до поверхні![]() .
.
Дивергенція має наступні властивості.
1.
![]() (Лінійність),
де
(Лінійність),
де
![]() -
постійні числа.
-
постійні числа.
2.Дивергенція
постійного вектора
![]() дорівнює нулю,
дорівнює нулю,
![]() .
.
3.Якщо
![]() -неперервно
диференційовна скалярна функція, то
має місце рівність
-неперервно
диференційовна скалярна функція, то
має місце рівність
![]() .
(6.7)
.
(6.7)
Дійсно,
якщо
![]() ,
то
,
то
![]() .
Підраховуючи
частинні похідні, отримуємо
.
Підраховуючи
частинні похідні, отримуємо
![]() ,
,
![]() ,
,
![]() .
.
Додаючи всі три рівності, приходимо до формули (6.7).
Приклади для самостійного завдання
Знайти
потік векторного поля
![]() через
зовнішню поверхню піраміди, утвореної
площиною
через
зовнішню поверхню піраміди, утвореної
площиною![]() та
координатними площинами, двома способами:
а)за означенням потоку;
б)за
допомогою формули Гауса-Остроградського.
та
координатними площинами, двома способами:
а)за означенням потоку;
б)за
допомогою формули Гауса-Остроградського.
1.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
2.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
3.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
4.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
5.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
6.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
7.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
8.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
9.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
10.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
11.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
12.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
13.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
14.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
15.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
16.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
17.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
18.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
19.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
20.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
21.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
22.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
23.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
24.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
25.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
26.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
27.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
28.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
29.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
30.![]() . (Відповідь:
. (Відповідь:![]() .
)
.
)
