
lecture_martyshev
.pdf
|
σ zmax |
|
= |
M x |
(5.14) |
|
|
||||
|
|
Wx |
|||
|
|
|
|
|
Здесь знак напряжений для расчетов на прочность роли не имеет и определяется по физическому смыслу (в растянутой зоне сечения «Å»). Для прямоугольного сечения шириной b и высотой h:
|
J x = |
bh3 |
, Wx = |
J x |
= |
bh2 |
|
||||||||
|
|
|
|
||||||||||||
Для круглого сечения радиуса R |
12 |
|
h/ 2 |
6 |
|
|
|||||||||
4 |
|
|
πR4 |
|
πR3 |
||||||||||
|
|
πR |
|
|
|
||||||||||
J x = |
J y = |
|
4 |
|
, Wx = Wy = |
4R = |
4 |
||||||||
Для кольцевого сечения с R и r |
|
|
|
|
|
|
|
|
|
|
|||||
J x = J y = |
π (R4 |
− r4 ), Wx = Wy |
= |
π |
(R4 − r 4 ), |
||||||||||
4R |
|||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||
Значения Wx для стандартных двутавров |
и швеллеров приводятся в |
||||||||||||||
таблицах ГОСТа.
Балки из хрупких материалов обычно изготавливают несимметричными относительно оси х. При этом, для равнопрочности их желательно, чтобы расстояния до крайних точек сечения от оси х были пропорциональны допускаемым напряжениям на растяжение и сжатие.
Нормальные и касательные напряжения в прямоугольном сечении балки при поперечном плоском изгибе
В отличие от чистого изгиба при поперечном изгибе в сечениях балки, наряду с нормальными напряжениями, появляются также и касательные напряжения, параллельные равнодействующей им силе
Qy = òτ yzdA
A
На основании закона парности касательных напряжений, последние возникают также и в продольных сечениях и вызывают сдвиги отдельных волокон относительно друг друга. Касательные напряжения в продольных сечениях обращаются в нуль на верхний и нижний поверхностях бруса и возрастают по какому-то закону к нейтральной оси.
Следовательно, поперечные сечения балки, плоские до деформации, при поперечном изгибе от M x , оставаясь плоскими, поворачиваются, а под
действием касательных напряжений, возникающих от Qy , искривляются.
Это искривление, в соответствии с характером изменения величины касательных напряжений, возрастает от краев балки к нейтральной оси (рис. 5.8). Следовательно, гипотеза плоских сечений при поперечном изгибе нарушается.
71

1) Рассмотрим случай, когда Qy = const по длине
Рис.5.8
волокна между этими сечениями не получат дополнительных удлинений по сравнению с удлинениями от изгиба сечения. Поэтому, в этом случае, для определения нормальных напряжений можно пользоваться формулой (5.12), полученной для чистого изгиба
2) Qy ¹ const, т.е. Qy меняется по длине балки.
В этом случае абсолютные сдвиги не одинаковы и, следовательно, за счет сдвига продольные волокна получают дополнительные удлинения и, значит, будет добавка в нормальных напряжениях. Однако, теоретические и экспериментальные исследования показали, что влияние указанного эффекта на величину нормальных напряжений невелико и им обычно на практике пренебрегают.
Таким образом, гипотеза плоских сечений условно распространяется также и на поперечный изгиб.
Следовательно, при поперечном изгибе, нормальные напряжения определяются по той же формуле чистого изгиба
σ z » M x y
J x
Относительно распределения касательных напряжений τ yz
Д.И. Журавским были сделаны следующие допущения:
1.Касательные напряжения в любой точке сечения направлены параллельно поперечной силе Qy ;
2.Касательные напряжения, действующие на одном и том же расстоянии от нейтральной оси х, равны между собой, т.е. по ширине сечения касательные напряжения распределяются равномерно.
Исследования показывают, что оба допущения оказываются
достаточно правильными для балок прямоугольного сечения, если высота балки больше ширины.
С учетом этих допущений и была получена формула Журавского в виде
τ yz = |
Qy × Sxотс |
|
(5.15) |
|
J xb |
||||
|
Sxотс − статический |
|||
Здесь: b − ширина сечения, где определяются τ yz ; |
||||
момент относительно оси х отсеченной части сечения.
Выясним характер распределения τ yz по высоте прямоугольного сечения балки (рис. 5.9), в котором действуют Qy > 0 (вниз).
72

|
|
|
|
Рис.5.9 |
|
|
|
|
|
|
|
|
|
|
||||
Найдем τ yz в произвольном сечении с-с |
на расстоянии у от оси х. |
|||||||||||||||||
Ниже сечения с-с будет отсеченная площадь |
Aотс (заштрихована на рис. |
|||||||||||||||||
5.9). Расстояние от оси х до центра тяжести Aотс обозначим Yc . Тогда |
||||||||||||||||||
S отс = A |
|
|
æ h |
|
ö 1 |
æ h |
|
|
ö |
|
b |
(h2 - 4y2 ) |
||||||
×Y = bç |
|
- y ÷ |
|
ç |
|
|
|
+ y ÷ |
= |
|
||||||||
|
|
|
|
|
|
|||||||||||||
x |
отс |
c |
|
è 2 |
|
ø 2 |
è 2 |
|
|
ø |
|
8 |
|
|||||
Из рис. 5.9 видно: |
|
|
|
|
|
|
|
|
||||||||||
|
æ h |
|
|
|
|
|
|
1 |
æ h |
|
|
|
|
|||||
|
|
|
|
ö |
|
|
|
|
ö |
|
||||||||
|
A = bç |
|
- y ÷, Y = |
|
|
ç |
|
+ y ÷ |
|
|||||||||
|
2 |
2 |
|
|
||||||||||||||
|
отс |
è |
|
|
ø |
c |
|
è 2 |
|
ø |
|
|||||||
Подставим Sxотс |
в формулу (5.15) |
|
Qy h2 - 4y2 |
|||
|
τ yz |
= |
||||
Видно, что τ yz |
J x |
|
8 |
|
||
|
|
|
||||
по высоте сечения |
(координате |
|||||
квадратной параболы. Для построения эпюры τ yz трех точек подсчитать по формуле (А)
1) |
y = 0 (точка на оси х) τ yz(1) |
=τ yzmax = |
Q |
y |
h2 |
|
8J x |
||||||
|
|
|
||||
(А)
у) меняется по закону поэтому надо не менее
2)y = h2 τ (yz2) = 0
3)y = h τ (3) = Qy 3h3
4 yz J x 32
По этим точкам строим нижнюю половину эпюры τ yz на рис. 5.9. Ввиду симметрии прямоугольника относительно оси х и эпюра τ yz симметрична относительно х. Напряжения τ yz распределены по сечению и направлены, как и Qy , вниз.
73

Касательные напряжения в двутавровом сечении
t |
Рис.5.10
Для стенки, вследствие малой ее ширины ( d ), допущения Журавского справедливы и τ yz в ней можно вычислить по (5.15). Для произвольного
сечения на расстоянии «у» от оси х в пределах стенки, т.е. 0 ≤ y ≤ k , где k = 0,5h − t , можно записать с учетом обозначений на рис. 5.10
S отс = A |
×Y |
+ A |
×Y |
= 0,5d(k 2 - y2 ) + bt(k + 0,5t) |
(В) |
|
x |
c |
c |
п |
п |
|
|
где: Ac = d (k − y), Yc = 0,5(k + y), |
Aп = bt, Yп = k + 0,5t |
|
||||
Подставляем (В) в формулу (5.15), в которой заменяем размер «b» на размер «d» - ширина стенки, получим расчетную формулу, по которой можно построить эпюру τ yz в стенке. Эпюра τ yz криволинейна (в (В) «у» в
квадрате), поэтому надо не менее трех точек. Считаем:
1)y = 0, по (В) находим Sxотс(1) , подставим в (5.15) и вычислим τ (yz1) =τ yzmax и откладываем ее в масштабе на эпюре τ yz рис. 5.10;
2)y = 0,5k , аналогично вычислим τ (yz2) ;
3)y = k , находим τ (yz3)
По этим точкам строим нижнюю часть эпюры |
τ yz , |
а т.к. двутавр |
симметричен относительно оси х, то и эпюра |
τ yz |
симметрична. |
Направление τ yz совпадает с направлением Qy . Если Qy |
> 0 (вниз), то и |
|
τ yz в стенке направлены вниз, а закон их изменения по высоте стенки показан на эпюре τ yz .
Полка двутавра широкая и малой высоты и допущения Журавского для нее несправедливы и, следовательно, пользоваться (5.15) нельзя.
В консолях полок возникают горизонтальные τ xz , которые можно найти по формуле
74
τ xz = |
Qy × Sxω |
(5.16) |
|
J x t |
|||
|
|
Определение Sωx поясним с помощью рис. 5.10.
На верхней левой консоли полки проведем сечение на расстоянии ω и в этом сечении найдем τ xz . Обозначим длину консоли полки m = 0,5b − 0,5d .
Тогда 0 ≤ ω ≤ m , |
Aω - отсеченная площадь |
|
|
|
|
|||
|
Sω = A |
×Y = tω(k + 0,5t) |
|
|
(С) |
|||
где |
x |
ω |
п |
|
|
|
|
|
|
Aω = t ×ω, |
Yп = k + 0,5t |
|
|
|
|||
|
|
|
|
|
||||
Из зависимости (С) видно, что |
Sxω |
линейно |
меняется |
по |
ω и, |
|||
следовательно, |
из (5.16) |
видно, что |
τ xz |
линейно |
меняются |
по |
длине |
|
консоли полки. Поэтому, для построения эпюры τ xz надо две точки:
1)ω = 0 (конец консоли), по (С) Sωx(1) = 0 и из (5.16) τ xz(1) = 0 .
2)ω = m , вычислим Sωx(2) и по (5.16) τ xz(2) =τ xzmax
Аналогичный закон изменения τ xz будет и в трех других консолях
полок. |
|
|
|
|
|
|
|
> 0 . |
Направления τ xz |
во всех полках показаны на рис. |
5.10 при |
Qy |
|||||
Они с τ yz |
в стенке составляют единый поток. Если τ yz |
направлены вниз |
||||||
(Qy > 0 ), |
то |
τ xz в |
верхней |
полке «сходятся», а |
в |
нижней |
полке |
|
«расходятся». |
Если |
Qy < 0 , |
направления τ yz и τ xz |
меняются |
на |
|||
противоположные. |
|
|
|
|
|
|
||
Условия прочности при поперечном изгибе.
Подбор сечений
Расчет балок на прочность обычно ведется по наибольшим нормальным напряжениям, возникающим в их поперечных сечениях.
Обозначая эти напряжения σ zmax , получим условие прочности
σzmax £[σ ]
I.Так как пластичные материалы одинаково сопротивляются как
растяжению, так и сжатию, то для них [σ р ] = [σсж ] = [σ ]. Поэтому балки из
пластичных материалов обычно имеют поперечные сечения, симметричные относительно своих нейтральных осей. Подбор сечения проводится из условия прочности действию наибольшего по абсолютной величине изгибающего момента
σ zmax = |
M xmax |
£ [σ ] |
(5.17) |
|
|||
|
|||
|
Wx |
|
|
Отсюда определяется необходимая величина момента сопротивления
75

Wxн ³ |
M xmax |
|
|
|
|
||
[σ ] |
|||
|
|||
Размеры сечения (при выбранной форме) подбираются так, чтобы его |
|||
момент сопротивления равнялся или был чуть больше требуемой |
|||
величины. |
|
|
|
При проектировании балки прямоугольного сечения, задаются |
|||
|
h |
|
|
|
bh2 |
|
|
h3 |
|
|
|
|
. |
||
соотношением сторон k = |
|
, тогда Wx = |
= |
|
|
и h = 3 |
6kWxн |
||||||||
b |
|
|
6k |
||||||||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
||||
|
|
πr |
3 |
|
|
|
|
4W н |
|
|
|
|
|||
Для круглого сечения Wx = |
|
|
|
, откуда |
r = 3 |
|
|
x |
. |
|
|
||||
4 |
|
|
π |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Подбор стальных балок прокатного профиля производится с помощью таблиц сортамента по величине Wx .
В случае применения тонкостенных профилей типа двутавра или деревянных прямоугольных сечений балок, при значительной поперечной нагрузке Qy , проводится проверка по максимальным касательным
напряжениям:
τ yzmax = |
Qymax |
× Sxотс(max) |
£ [τ ] |
(5.18) |
|
|
|
||||
J x × b |
|||||
|
|
|
|||
[σ ] и [τ ] берутся из нормативных документов для каждого материала.
Подобранные сечения балки должны удовлетворять условиям прочности как по нормальным (5.17), так и по касательным напряжениям
(5.18). Для деревянных балок расчет на прочность по τ yzmax может иметь
решающее значение, т.к. дерево плохо сопротивляется скалыванию вдоль волокон. Допускается перегрузка до 5% от [σ ] и [τ ].
Балки из хрупких материалов, плохо работающих на растяжение, изготавливают обычно с несимметричным относительно оси х сечением
(см. рис) и составляют два |
||||||||
условия прочности в растянутой и |
||||||||
сжатой зонах: |
M xmax |
|
|
|
||||
|
σ zрmax = |
ymaxр |
£ [σ р ], |
|||||
|
||||||||
|
|
|
|
J x |
|
|
|
|
|
σ zсжmax = |
M xmax |
ymaxсж |
³ [σ сж ], |
||||
|
||||||||
|
|
|
|
J x |
[σ сж ] |
|
||
Здесь учтено, что |
отрица- |
|||||||
тельная величина |
и по |
|
модулю |
|||||
|
[σ сж ] |
|
> [σ р ]. Поэтому при проек- |
|||||
|
|
|||||||
тировании таких сечений, необходимо, чтобы |
ymaxсж > ymaxр |
, |
а для |
|||||
равнопрочности желательно, чтобы |
|
|
|
|
||||
76

ymaxсж / ymaxр ≈ [σ сж ]/[σ р ]
В железобетонных балках растянутая зона армируется металлом, чтобы увеличить [σр ].
Определение деформации балок при изгибе
Прогиб и поворот сечения балки
При действии внешних сил, расположенных в одной из главных плоскостей инерции сечения балки, наблюдается искривление ее оси в той же плоскости, происходит плоский изгиб.
На рис. изображена искривленная ось балки в плоскости YOZ , защемленной одним концом и нагруженной на другом конце силой F . Центр тяжести С какого-либо сечения с абсциссой z при деформации балки переместится в т. C1.
Перемещение CC1 ц.т. сечения по направлению, перпендикулярному
к оси балки, называется прогибом балки в этом сечении. Прогиб обозначается буквой V .
V = CC1
При деформации балки сечение поворачивается на некоторый угол θ ,
который называется углом поворота сечения.
Обе величины, определяющие деформации балки, являются функцией от Z .
Уравнение V = f (z) − представляет собой уравнение кривой, по
которой изогнется ось балки, это будет уравнение изогнутой оси балки. Касательная к изогнутой оси балки в т. C1 составит с осью Z угол,
равный θ . С другой стороны, тангенс угла, образованного касательной к кривой V = f (z) и осью Z , как известно, равен
tgθ = |
dV |
|
|
|
|||
dz |
|
|
|
||||
|
|
|
|
|
|
||
Так как на практике прогибы балки обычно малы по сравнению с |
|||||||
длиной балки, то углы θ малы. |
|
|
|
||||
Для таких углов можно считать, что тангенс угла равен самому углу, |
|||||||
выраженному в радианах. Следовательно |
|
|
|
||||
|
dV |
|
′ |
|
|||
θ = dz = V |
(5.19) |
||||||
|
|
||||||
При выбранных нами направлениях координатных осей |
(см. рис) |
||||||
положительный прогиб будет вниз, а положительный угол поворота сечения θ – по направлению вращения часовой стрелки.
77
Дифференциальное уравнение изогнутой оси балки
Для получения зависимости V = f (z) надо установить, как зависят
деформации балки от внешних сил, изгибающих ее, от размеров и материала балки.
Такая зависимость была получена нами ранее при выводе формулы нормальных напряжений при изгибе в виде связи кривизны оси балки с изгибающим моментом (5.11):
1 |
= |
M x |
(а) |
ρ |
EJ x |
где ρ − радиус кривизны изогнутой оси балки.
Однако в общем случае использовать зависимость (а) для определения прогибов не удается.
С другой стороны, из курса высшей математики известна зависимость
между радиусом кривизны плоской кривой и координатами |
Z и V |
ее |
||||||||
точек: |
1 |
|
|
|
V ′′ |
|
|
|
|
|
|
|
= ± |
|
|
|
|
(б) |
|||
|
|
ρ |
(1 + (V ′)2 )3 / 2 |
|
|
|
||||
Приравнивая выражения (а) и (б) исключим радиус кривизны: |
|
|
||||||||
|
|
|
|
M x |
= ± |
V ′′ |
|
|
|
(в) |
|
|
|
EJ x |
(1+ (V ′)2 )3 / 2 |
|
|
||||
Это |
дифференциальное |
уравнение |
изогнутой |
оси, |
или |
|||||
дифференциальное уравнение упругой линии.
Выше мы уже отмечали, что V ′ =θ – величины очень малые, поэтому их квадратом можно пренебречь по сравнению с единицей. Тогда
уравнение (в) упростится |
|
± EJ xV ′′ ≈ M x |
(г) |
Это приближенное дифференциальное уравнение изогнутой оси. Правило знаков для изгибающего момента M x установлено ранее.
Знак в формуле (г) зависит от выбора направлений осей координат. В нашем случае, когда ось z горизонтальна и направлена вправо, а ось y −
вниз, надо брать знак «–». Итак |
|
EJ xV ′′ = −M x |
(5.20) |
Если ось у направлена вверх, надо взять знак «+». |
|
Интегрирование дифференциального уравнения упругой линии
Для того, чтобы получить аналитические выражения для прогибов и углов поворота необходимо найти решение дифференциального уравнения (5.20). Правая часть уравнения является известной функцией для каждой конкретной балки с конкретным загружением. Интегрируя его один раз, получим:
EJxV ′ = EJxθ = −ò M xdz + C
78
Это выражение определяет закон изменения углов поворота сечений балки.
После повторного интегрирования найдем уравнение оси балки
EJxV = −ò dzò M xdz + Cz + D
Постоянные интегрирования С и D находятся из граничных условий. Уравнения (5.20) записываются для каждого участка балки и
интегрируются. При большом числе участков определение const Ci и Di
осложняется, т.к. приходится решать большое число совместных алгебраических уравнений, из которых они вычисляются. Поэтому для таких балок были разработаны другие методы.
Один из таких методов сводится к уравниванию однотипных const интегрирования, для чего, при составлении аналитических выражений изгибающих моментов M x по участкам балки, необходимо соблюдать ряд
условий.
Метод уравнивания произвольных постоянных (метод Клебша)
Равенство между собой произвольных постоянных (C1 = C2 = ... = C и D1 = D2 = ... = D ) при большом числе участков балки возможно при соблюдении следующих условий:
1)Отсчет координат Si всех участков должен вестись от одного конца балки.
2)Все составляющие выражения M x предыдущего участка, должны сохраняться неизменными в выражениях M x последующего участка. Поэтому, если на каком-то участке появляется распределенная нагрузка q , не идущая до конца балки, то ее надо продлить до конца
балки, добавив на этих же участках такую же распределенную нагрузку с противоположном знаком.
3)Сосредоточенные моменты m0 вводятся в виде m0 (Si − d)0 , где d − расстояние от начала балки до сечения, где приложены m0 .
4)Интегрирование дифференциальных уравнений должно вестись без раскрытия скобок.
Поясним выполнение перечисленных условий на примере:
Пример (рис.5.11):
Дано: l1 = 1,5м; l2 = 4,5м; l3 = 4м; F = 20кН; q = 45кН/м; m0 = 20кНм; E = 2 ×104 кН/см2; [σ ]=16кН/см2; [τ ]=10кН/см2;
79
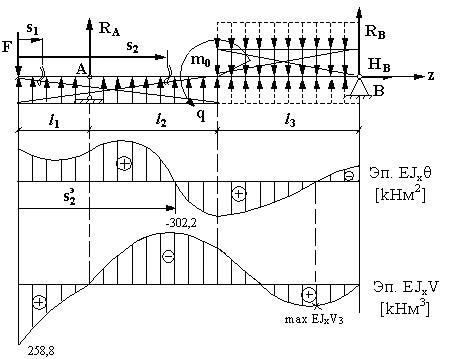
Рис.5.11
На рис. 5.11 сплошными линиями и перечеркнутыми показаны нагрузки q − заданные, а пунктиром показаны добавки нагрузок q
согласно п.2 метода Клебша. Сначала учитываем только заданные нагрузки q . По правилам, показанным при решении примера 1 на рис. 5.5,
находим:
1)Из уравнений равновесия всей балки при заданных нагрузках находим все опорные реакции: RA = -154,12кН; RB = 84,12кН; H B = 0.
2) Строим эпюру Qy и эпюру M x , из которых находим
M xmax =-105,68кНм и Qymax =-106,62кН
Для балки подберем стандартный двутавр:
Из условия прочности балки (5.17) находим
Wxн ³ |
M xmax |
= |
|
|
105,68 ×100 |
=660,5см2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
[σ ] |
|
16 |
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||
Из таблиц сортамента двутавров видно, что Wxн лежит между: №33 |
|||||||||||||||||
Wxт =597см3 и №36 Wxт =743см3. |
|
|
Cначала проверим №33 с учетом |
||||||||||||||
допускаемой перегрузки 5% от [σ ], т.е. [σ ]=16¸16,8кН/см2. |
|||||||||||||||||
σ zmax = |
|
M xmax |
|
|
= |
10568 |
= 17,7кН/см2 |
||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Wxт |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
597 |
|
|
|||||||
Итак, №33 не подходит балке даже с учетом перегрузки. |
|||||||||||||||||
Проверяем №36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
σ zmax = |
|
M xmax |
|
|
= |
10568 |
=14,22 £ [σ ] = 16кН/см2 |
||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|||||||||||||
|
Wxт |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
743 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
80 |
||||||
