
lecture_martyshev
.pdf
оказались положительными, их направления M xa , Qya , M xb и Qby показаны
на рис.10.6. Сечения «а» и «b» концы балки, поэтому ВСФ в них должны быть равны нулю. Этого можно добиться, приложив в этих сечениях
внешние Q0a , M0a , Q0b и M0b , равные и противоположно направленные ВСФ (рис.10.6). Балку на рис.2) надо рассчитать дважды: 1) от Q0a и M0a при оси z вправо; 2) от Qby и M xb при оси z влево по формулам (10.7) и
(10.8) полубесконечной балки и построить по ним эпюры. Итоговые значения Qy и M x получим, суммируя эпюры от вышеуказанных трех
расчетов. При очень короткой балке на итоговых эпюрах Qy и M x в
сечениях «а» и «b» балки ВСФ могут оказаться значительными (а должны быть равны нулю). Поэтому еще раз надо повторить два расчета балки по схеме рис.2, приложив на торцах балки внешние Q0 и M0 , равные и
противоположно направленные ВСФ итоговых эпюр. Полученные эпюры Qy и M x суммируем с имеющимися итоговыми. Отличие Qy и M x от
нулевых значений на торцах балки уменьшится. На практике обычно бывает достаточно одного или двух приближений для получения приемлемых результатов.
IV. Расчет балок по линиям влияния
Бесконечная длинная балка на упругом основании показана на рис.10.7 как горизонтальная штрихпунктирная линия. Пусть на нее в т.О действует сила
Рис.10.7 F = 1. По (10.5) для балки можно построить эпюру M x , которая на рис.10.7 показана сплошной
линией. Величина M KO определяет M x в произвольной т.K (с координатой zK ) от силы F = 1 приложенной в т.О. Если силу F = 1 приложить в т.K, то эпюру M x можно изобразить пунктирной линией. Величина MOK определяет M x в т.О от силы F = 1, приложенной в т.K. Ввиду симметрии эпюры M x очевидно, что MOK = M KO . Этот вывод
справедлив для любого положения силы F = 1, т.е. сплошная линия изображает закон изменения M x в т.О от движения силы F = 1 вдоль
балки. Сплошную линию на рис.10.7 называют линией влияния.
Пусть на балку действует произвольная нагрузка (рис.10.8). В произвольном сечении (т.О) найти M x от этой нагрузки.
В интересующем нас сечении (т.О) расположим начало координат и строим эпюру M x от действия в этой точке силы F = 1. Получим линию
влияния. Под силами F1, F2 и Fm определяем с учетом знаков M10, M 20 и
141
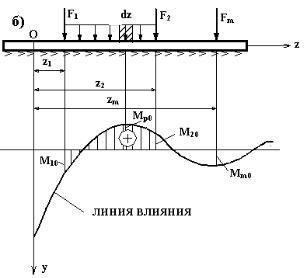
M m0 . В сечении т.О суммированием
ρ
 ρ
ρ
изгибающий момент M x найдем алгебраическим
M x = F1 × M10 + F2 × M 20 + FmM m0 |
(23) |
Если участок балки нагружен внешней погонной нагрузкой p = const (рис.10.8), то разбивая ее
на малые силы pdz и определяя от них на линии влияния M p0 , по
аналогии с (23) найдем
M x = å pdzM p0 =
z2 |
|
= ò pM p0dz = |
(24) |
z1 |
|
|
z2 |
Рис.10.8 |
= p ò M p0dz = pw |
z1 |
|
Здесь ω − заштрихованная |
площадь линии влияния под нагрузкой p |
(определяется с учетом знаков). В справочниках приводятся таблицы для вычисления ω . Можно использовать численные методы при помощи ЭВМ.
Аналогично можно построить линию влияния прогибов V и по ней определять прогибы в любом сечении балки.
Эпюра Qy обратносимметрична относительно F = 1, поэтому QKO = - QOK , и линия влияния Qy отличается знаком от самой эпюры Qy .
Для коротких балок можно уточнить решение, используя вышеизложенный метод последовательных приближений.
142

т. A1 , т.е. получит перемещения u и v . Точка B1 |
получит перемещения: |
|||||||||||||
u + |
∂u |
dx (вдоль оси x ) и v + |
|
∂v |
dx (вдоль оси |
y ). Точка C переместится |
||||||||
|
|
|||||||||||||
|
¶x |
|
|
|
¶x |
|
|
|
|
1 |
||||
|
|
|
|
|
|
|
|
|
||||||
на u + |
∂u |
dy (вдоль оси x ) и |
v + |
|
∂v |
dy (вдоль оси |
y ). Из рис. 11.1 отрезок |
|||||||
|
¶y |
|||||||||||||
|
|
|
¶y |
|
|
|
|
|
|
|
|
|
||
æ |
¶u |
ö |
|
|
|
¶u |
dx » A1B1 |
ввиду малости угла α1 |
||||||
A1B2 = dx + çu + |
¶x |
dx÷ - u = dx + |
¶x |
|||||||||||
è |
ø |
|
|
|
|
|
|
|||||||
(деформации тела считаются малыми). Относительная деформация ребра АВ вдоль оси x равна
ε x = (A1B1 - |
|
ææ |
|
¶u |
|
ö |
|
ö |
|
¶u |
» ε x |
|
(1) |
|||||||||
AB) / AB = ççdx + |
¶x |
dx ÷ |
- dx÷ / dx = |
¶x |
|
|||||||||||||||||
|
|
|
|
|
|
èè |
|
|
ø |
|
ø |
|
|
|
|
|
|
|||||
Аналогично для ребра AC = dy , относительная деформация вдоль оси y |
|
|||||||||||||||||||||
будет ε |
|
|
, с учетом A C |
» A C |
|
|
|
æ |
|
|
¶v |
ö |
|
|
|
|
|
¶v |
dy |
|
||
y |
2 |
= dy + çv + |
|
dy ÷ - v = dy + |
|
|
||||||||||||||||
|
|
|
1 1 |
1 |
|
|
ç |
|
|
¶y |
÷ |
|
|
|
|
|
¶y |
|
|
|||
|
|
|
|
|
|
|
|
|
|
è |
|
|
ø |
|
|
|
|
|
|
|
||
ε |
|
|
= (A C - |
AC) / AC = |
ææ |
|
¶v |
ö |
ö |
/ dy = |
¶v |
» ε |
|
(2) |
||||||||
y |
ççdy + |
|
|
dy ÷ - dy ÷ |
|
|
y |
|||||||||||||||
|
|
1 1 |
|
|
çç |
|
¶y |
÷ |
÷ |
|
|
¶y |
|
|
|
|||||||
|
|
|
|
|
|
|
èè |
|
ø |
ø |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
143 |

Аналогично получим ε z − линейную деформацию вдоль оси z третьего ребра элемента (не показанного на рис.11.1)
|
|
|
|
|
|
|
|
ε z = |
∂w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3) |
|
|
|
|
|
|
|
|
¶z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ввиду малости угла α1 можно записать (из рис.11.1) |
|
|
|
|
|
|
|
|||||||||||||||||
α |
|
» tgα |
|
= B B |
/ A B |
= |
¶v |
æ |
|
¶u |
ö |
= |
¶v |
æ |
+ |
¶u ö |
¶v |
/(1+ ε |
|
) (4) |
||||
|
|
¶x |
dx /çdx + |
¶x |
dx÷ |
¶x |
/ç1 |
|
÷ = |
¶x |
x |
|||||||||||||
|
1 |
|
1 |
1 2 |
1 2 |
|
è |
|
ø |
|
è |
|
¶x ø |
|
|
|||||||||
Деформации тела малы, поэтому |
ε x много меньше 1 |
и |
ε x |
можно не |
||||||||||||||||||||
учитывать. Тогда (4) упростится |
|
|
∂v |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
α1 » |
|
|
|
|
|
|
|
|
|
(5) |
|||||
Аналогично найдем |
|
|
|
¶x |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
∂u |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
α2 » |
|
|
|
|
|
|
|
|
|
|
(6) |
||||
|
|
|
|
|
|
|
|
|
|
¶y |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
XOY называется |
|||||||
Известно, что изменение прямого угла САВ в плоскости |
||||||||||||||||||||||||
сдвигом в плоскости XOY и обозначается γ xy . Следовательноγ xy = α1 +α2 . С учетом (5) и (6) получим
γ xy = |
∂u |
+ |
∂v |
(7) |
|
¶y |
¶x |
||||
|
|
|
Аналогично можно получить γ xz − сдвиг в плоскости XOZ , γ yz − сдвиг в
плоскости YOZ .
Итак, деформацию в любой точке тела определяют шесть величин, которые с учетом (1), (2), (3) и (7) можно записать так
1) ε x = ∂¶ux , 4) γ xy = ∂¶uy + ∂¶vx
2) ε y = |
¶v |
, |
5) γ yz = |
¶v |
|
+ |
¶w |
|
(11.1) |
|
¶y |
¶z |
|
¶y |
|||||||
|
|
|
|
|
|
|||||
3) ε z = |
¶w |
, |
6) γ zx = |
¶u |
+ |
|
¶w |
|
||
¶z |
¶z |
|
¶x |
|
||||||
|
|
|
|
|
|
|||||
Это и есть уравнения Коши.
II. Условия совместности (неразрывности) деформаций
Представим себе тело, разрезанным на малые параллелепипеды. Если каждый из этих параллелепипедов получит произвольные деформации, то из деформированных параллелепипедов не удастся вновь сложить сплошное тело: во многих точках возникнут щели, пустоты. Следовательно, при деформации тела εx , ε y , εz , γ xy , γ xz , γ yz должны быть
связаны определенными зависимостями. Получим их.
Из (11.1) первое дифференцируем дважды по y , второе – дважды по x и сложим их
144

|
|
¶2ε |
x + |
|
¶2ε y |
|
|
|
|
¶3u |
|
|
|
¶3v |
|
|
|
|
¶2 æ |
¶u |
|
¶v ö |
(а) |
||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
+ |
|
|
|
|
|
|
= |
|
|
|
ç |
|
|
+ |
÷ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
¶y2 |
|
|
¶x2 |
|
|
|
|
¶x¶y2 |
|
|
|
|
|
|
|
|
|
|
|
|
ç |
¶y |
|
÷ |
|
||||||||
|
|
|
|
|
|
|
|
|
|
¶x2¶y ¶x¶y è |
|
¶x ø |
|
||||||||||||||||||||||
Выражение в скобках по 4) из (11.1) равно γ xy . Тогда |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
¶2ε |
x |
+ |
¶2ε y |
= |
|
¶2γ xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
(в) |
|||||||||
|
|
|
|
|
|
|
|
|
|
¶x2 |
|
¶x¶y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
¶y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Аналогично можно составить еще два соотношения |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
¶2ε y |
+ |
¶ |
2ε |
z |
= |
¶2γ yz |
|
; |
|
¶2ε |
z |
+ |
|
¶2ε |
x |
= |
¶2γ |
zx |
|
|
|
(г) |
||||||||||||
|
¶z2 |
¶y2 |
¶y¶z |
|
|
|
|
|
|
|
|
|
¶z2 |
¶z¶x |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
¶x2 |
|
|
|
|
|
|
|||||||||||||||||||||
Эти соотношения легко записать, используя кольцевую перестановку индексов x, y, z.
Для однозначности, шесть деформаций должны быть связаны шестью зависимостями.
Продифференцируем три последних уравнения (11.1) так:
¶γ xy = ¶2u + ¶2v ¶z ¶y¶z ¶x¶z
¶γ yz = ¶2v + ¶2w ¶x ¶x¶z ¶x¶y
¶γ zx = ¶2u + ¶2w ¶y ¶y¶z ¶x¶y
Сложим два первых соотношения и вычтем третье:
¶γ xy + ¶γ yz - ¶γ zx = 2 ¶2v ¶z ¶x ¶y ¶x¶z
Продифференцируем это уравнение еще раз по y и, учитывая, что по 2) из (11.1) ε y = ∂v / ∂y получим
¶ |
æ |
¶γ |
xy + |
¶γ |
yz - |
¶γ zx |
||
ç |
|
|
||||||
|
ç |
¶z |
|
¶x |
|
¶y |
||
¶y è |
||||||||
ö
÷ =
÷
ø
|
¶ |
3 |
v |
|
¶ |
2 |
æ |
¶v |
ö |
¶2ε |
y |
|
2 |
|
= 2 |
|
ç |
÷ = 2 |
|
(д) |
|||||
|
|
|
|
|
|
|
|
|||||
|
¶x¶y¶z |
|
|
|
ç |
¶y |
÷ |
¶x¶z |
|
|||
|
|
¶x¶z è |
ø |
|
||||||||
Аналогично можно получить еще два уравнения, используя кольцевую перестановку индексов. Итак, окончательно получим шесть уравнений (в), (г) и (д), которые и называют условиями совместности (неразрывности) деформаций или уравнениями Сен-Венана.
145

|
|
|
|
|
¶2ε |
x |
+ |
¶2ε y |
|
= |
¶ |
2γ xy |
|
|
; |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
¶x2 |
|
¶x¶y |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
¶y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
¶2ε y |
|
+ |
¶2ε |
z |
|
|
= |
¶ |
2γ yz |
|
; |
|
|
|
(11.2) |
|||||||||||||
|
|
|
|
|
|
¶z2 |
|
|
|
¶y2 |
|
¶y¶z |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
¶2ε z |
|
+ ¶2ε x |
= |
¶2γ zx |
|
; |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
¶x2 |
|
|
|
|
|
¶z2 |
|
|
¶z¶x |
|
|
|
|
|
|
|
|
||||||||||
¶ |
æ ¶γ xy |
|
|
¶γ yz |
|
|
|
|
¶γ |
|
ö |
|
|
¶2ε y |
|
||||||||||||||||||
|
ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zx |
÷ |
= 2 |
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
ç |
|
¶z |
|
|
|
|
¶x |
|
|
|
¶y |
÷ |
|
¶x¶z |
||||||||||||||||||
¶y è |
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
||||||||||||||||||
¶ |
æ |
|
¶γ yz |
|
|
|
¶γ |
zx |
|
|
|
¶γ xy ö |
|
¶2ε |
z |
|
|
||||||||||||||||
|
ç |
|
|
|
|
|
+ |
|
|
|
|
- |
|
|
|
|
|
|
÷ |
= 2 |
|
|
|
|
|
; |
|||||||
|
ç |
|
¶x |
|
|
|
¶y |
|
|
|
¶z |
÷ |
¶y¶x |
||||||||||||||||||||
¶z è |
|
|
|
|
|
|
|
|
|
|
ø |
|
|
||||||||||||||||||||
¶ |
æ |
|
¶γ |
zx |
|
|
|
¶γ xy |
|
|
|
¶γ yz ö |
|
|
¶ |
2ε |
x |
|
|||||||||||||||
|
ç |
|
|
|
+ |
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
÷ |
= 2 |
|
|
|
|
|
. |
||||||
|
ç |
|
¶y |
|
|
|
¶z |
|
|
|
|
¶x |
|
÷ |
|
¶z¶y |
|||||||||||||||||
¶x è |
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|||||||||||||||||||
III. Дифференциальные уравнения равновесия
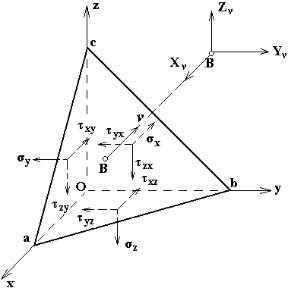
Рис.11.2
Вырежем из нагруженного тела малый прямоугольный элемент с ребрами dx, dy, dz , параллельными осям x, y, z . Со стороны отброшенных
частей на элемент действуют напряжения, определяемые тензором напряжений Tσ , который в разделе 1 обозначен как формула (1.2). На
невидимых гранях (рис.11.2) действуют σ x , σ y , ..., τ xz . На рис.11.2 эти напряжения условно вынесены за пределы элемента (чтобы упростить
146

рисунок). В разделе 1 приняты следующие обозначения и правила: σ x − нормальное напряжение вдоль оси x , τ xz − касательное напряжение вдоль
оси x , действующее на площадке, перпендикулярной оси z . Аналогично определяются и другие напряжения. Площадки положительны, если внешние нормали к ним направлены вдоль осей. На положительных площадках положительные напряжения направлены вдоль осей x, y, z , на
отрицательных – против осей.
Невидимые площадки – отрицательные, поэтому положительные напряжения σ x , σ y , ..., τ xz направлены против осей (рис.11.2).
Видимые площадки – положительные и все напряжения на них направлены вдоль осей и имеют добавки по соответствующей координате. Например, на невидимой грани, перпендикулярной оси x , действуют σ x
(против оси x ), а на видимой грани, отстоящей от невидимой на малом расстоянии dx , действуют σ x + ∂¶σxx dx (вдоль оси x ). Аналогично и на
других парах граней.
Кроме напряжений на элемент тела действуют объемные силы, их проекции на координатные оси обозначим: X , Y, Z . Эти силы отнесены к
единице объема. Объем элемента dV = dxdydz . Тогда силы, действующие в
объеме всего элемента, будут равны: |
|
Xdxdydz, Ydxdydz, Zdxdydz |
(1) |
Элемент вырезан из нагруженного тела, находящегося в равновесии. Поэтому и малый элемент, под действием всех напряжений, указанных на рис. 11.2 и объемных сил (1), должен быть в равновесии. Следовательно, должны удовлетворятся шесть уравнений статики. Рассмотрим уравнение
проекций сил на ось x . |
|
Каждое напряжение надо умножать на площадь |
||||||||
грани, где оно действует, т.е. рассматривать силы на гранях. |
|
|||||||||
æ |
|
¶σ |
x |
|
ö |
|
æ |
¶τ xy |
|
ö |
|
|
|
|
|
|
ç |
|
|
÷ |
|
Sx = 0. çσ x + |
|
|
|
|
|
|
|
|||
¶x |
dx÷dzdy -σ xdzdy + çτ xy + |
¶y |
dy ÷dxdz - |
|||||||
è |
|
|
ø |
|
è |
|
ø |
|||
-τ xydxdz + |
æ |
|
|
|
¶τ |
|
ö |
|
|
|
çτ xz + |
|
xz dz ÷dxdy -τ xzdxdy + Xdxdydz = 0 |
||||||||
|
è |
|
|
|
¶z |
ø |
|
|
|
|
После раскрытия скобок, приведения подобных членов и деления на объем dV = dxdydz получим
¶σ |
x + |
∂τ xy |
+ |
¶τ |
xz + X = 0 |
(2) |
|
¶y |
|
||||
¶x |
|
¶z |
|
|||
Аналогично, составив Σy = 0 и Σz = 0 , можно получить еще два уравнения
статики. Проще их записать сразу, используя указанную выше кольцевую перестановку x, y, z .
В итоге получим три уравнения равновесия малого прямоугольного элемента, вырезанного внутри тела.
147
∂σ |
x + |
∂τ xy |
+ |
∂τ |
xz + X = 0 |
|
|||||||
|
|
|
∂y |
|
|
|
|||||||
∂x |
|
|
|
|
∂z |
|
|
|
|||||
∂τ yx |
+ |
|
∂σ y |
|
+ |
|
∂τ yz |
+ Y = 0 |
(11.3) |
||||
|
|
∂y |
|
|
|||||||||
∂x |
|
|
|
|
∂z |
|
|||||||
∂τ |
zx + |
|
∂τ zy |
|
+ |
|
∂σ |
z + Z = 0 |
|
||||
|
|
∂y |
|
|
∂z |
|
|||||||
∂x |
|
|
|
|
|
|
|
||||||
Можно составить еще три уравнения равновесия моментов относительно осей x, y, z по выше указанному правилу и убедиться, что они дадут уже
известный нам закон парности касательных напряжений (1.3),
полученный в разделе 1
τ yz =τ zy , τ xy =τ yx , τ xz =τ zx
IV. Напряжения на наклонных площадках (Условия на поверхности)
Вырежем из нагруженного тела бесконечно малый тетраэдр oabc с тремя плоскостями, совпадающими с координатными (см. рис. 11.3). Положение в пространстве наклонной площадки abc определяется нормалью ν , направляющие конусы которой обозначим так:
l = cos(x, ν), m = cos( y, ν),
|
|
n = cos(z, ν) |
|
|
|
Площадку abc обозначим dA. |
|
a |
|||
|
|
Невидимые треугольные площадки, |
|
|
Рис.11.3 |
перпендикулярные осям x, y и z , |
|
|
обозначим и определим так: |
|
|
dAx = dAobc = dA×l, dAy = dAoac = dA× m, dAz = dAoab = dA× n |
(а) |
||
На этих невидимых, отрицательных площадках, действуют положительные напряжения, определяемые Tσ (см. п.III). На наклонной площадке abc
действуют компоненты полного напряжения Xν , Yν и Zν . Под действием
всех напряжений, показанных на рис.11.3, тетраэдр находится в равновесии. Умножая напряжения на площадки, составим уравнение статики
Sx = 0. Xν ×dA -σ xdAx -τ xydAy -τ xzdAz = 0 |
(в) |
Объемные силы X , Y и Z здесь не учитываются, |
т.к. они |
пропорциональны объему, который имеет третий порядок малости, а все слагаемые в (в) – второй порядок малости. Подставляя (а) в (в) и сокращая на dA получим
148
Xν = σ xl +τ xym +τ xzn (г)
Составляя уравнения статики Σy = 0 и Σz = 0 , получим еще два уравнения,
которые легко |
записать, используя кольцевую |
перестановку |
x, y, z |
и |
l, m, n , получим три уравнения равновесия тетраэдра |
|
|
||
|
Xν = σ xl +τ xym +τ xzn |
|
|
|
|
Yν =τ yxl + σ ym +τ yzn |
|
(11.4) |
|
|
Zν =τ zxl +τ zym + σ zn |
|
|
|
Если площадка |
abc совпадает с поверхностью |
тела, то Xν , |
Yν и |
Zν |
соответствуют компонентам внешней нагрузки. В этом случае уравнения (11.4) называют условиями на поверхности тела. Они связывают внешние напряжения с внутренними в теле.
Удовлетворение условиям (11.3) и (11.4) является необходимым и достаточным условием равновесия в любой точке тела (внутри и на поверхности).
149
РАЗДЕЛ 12 АНАЛИЗ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО
СОСТОЯНИЯ В ТОЧКЕ ТЕЛА
I. Объемное напряженное состояние
1. Полное, нормальное и касательное напряжения на наклонной площадке
На рис. 11.3 показаны компоненты полного напряжения ρν на
наклонной площадке abc. Очевидно, что его численное значение определяется так
|
|
|
|
|
|
|
ρ |
2 = X |
2 |
+ Y |
2 + Z 2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
ν |
ν |
ν |
ν |
|
|
|
|
|
|
|||
Подставляя сюда формулы (11.4) найдем |
|
|
|
|
|
|
|
|
|||||||||||
ρ 2 = (σ |
x |
l +τ |
xy |
m +τ |
xz |
n)2 + (τ |
yx |
l + σ |
y |
m +τ |
yz |
n)2 + (τ |
zx |
l +τ |
zy |
m + σ |
z |
n)2 (12.1) |
|
ν |
|
|
|
|
|
|
|
|
|
|
|||||||||
Здесь l = cos(x, ν ), m = cos (y, ν ) и |
n = cos(z, ν ) – направляющие конусы |
||||||||||||||||||
нормали ν |
|
к площадке abc. Полное напряжение ρν |
можно разложить на |
||||||||||||||||
σν − нормальное и τν − касательное напряжения на наклонной площадке.
Очевидно, что ρ2 |
= σ 2 |
+τ 2 . |
Напряжение σ |
ν |
можно найти, проектируя |
ν |
ν |
ν |
|
|
|
Xν , Yν и Zν на нормаль ν , |
т.е. σν = Xν l + Yν m + Zν n . С учетом формул |
||||
(11.4) получим |
|
|
|
|
|
σν = (σ xl +τ xym +τ xzn)l + (τ yxl +σ ym +τ yzn)m + (τ zxl +τ zym +σ zn)n |
(12.2) |
||
Касательное напряжение τν можно найти так |
|
|
|
τ 2 |
= ρ2 −σ |
2 |
(12.3) |
ν |
ν |
ν |
|
2. Главные напряжения, главные площадки На наклонной площадке, у которой орт нормали ν совпадает с
направлением ρν , величина τν = 0 , а σν будет экстремально и равно ρν .
Такая площадка называется главной (ее направление определяют направляющие косинусы, которые обозначим l0, m0, n0 ). А напряжения на
ней обозначим σ0 = ρν . Все его проекции на оси x, y, z будут Xν = σ0l0, Yν = σ0m0, Zν = σ0n0 . Подставим их в формулы (11.4)
σ0l0 = σ xl0 +τ xym0 +τ xzn0 |
(σ x −σ0 )l0 +τ xym0 +τ xzn0 = 0 |
σ0m0 =τ yxl0 + σ ym0 +τ yzn0 |
или τ yxl0 + (σ y − σ0 )m0 +τ yzn0 = 0 (1) |
σ0n0 = τ zxl0 +τ zym0 +σ zn0 |
τ zxl0 +τ zym0 + (σ z −σ0 )n0 = 0 |
Надо найти σ0 и l0, m0, n0 при известных напряжениях в точке тела σ x ,
σ y , σ z , τ xy , τ xz , τ yz .
Очевидно, что l02 + m02 + n02 =1.
150
