
lecture_martyshev
.pdf
известно, определяется так U = 1 |
Р ×D . Сила Р прикладывается в т. К, |
|||
|
2 |
д |
д |
|
куда падает груз P . По закону сохранения энергии A = U , т.е. |
|
|||
P(h + D) = 1 |
Р ×D |
(7) |
||
|
|
2 |
д |
|
Из (6) Рд = Р × Kд , подставим в (7) получим |
|
|||
P(h + D) = 1 |
Р × Kд × D |
(8) |
||
|
|
2 |
|
|
Сокращаем на P и учитывая из (9.4), что Kд = D / Dcт найдем |
|
|||
2(h + D) = D2 / Dcт |
или |
D2 - 2Dcт × D - 2hDcт = 0 |
(9) |
|
Относительно неизвестной |
получили стандартное квадратное уравнение |
|||
типа x2 + bx + c = 0 |
|
|
|
|
Здесь b = -2Dcт , c = -2hDcт . |
Решение квадратного уравнения известно из |
|||||
справочников: x = D = - |
b |
± |
æ b |
ö |
2 |
|
2 |
ç |
÷ |
- c . В нашем случае получим |
|||
|
|
è 2 |
ø |
|
|
|
|
|
|
D = Dcт ± D2ст + 2hDcт |
(10) |
|
При ударе всегда D > Dcт , поэтому выбираем знак (+) и формулу (10) преобразуем так
D = Dcт + Dcт |
1+ 2h / Dcт |
или окончательно D = Dcт (1+ |
1+ 2h / Dcт |
) |
(11) |
|||
Согласно (9.4) Kд = D / Dcт , тогда из (11) получим |
|
|
|
|||||
|
|
|
Kд =1+ |
|
|
(9.8) |
||
|
|
|
1+ 2h / Dcт |
|||||
Величина |
ст - статическая деформация бруса в |
точке удара |
от |
|||||
статического приложения силы P в точке «K» падения груза весом |
P . |
|||||||
Определяется известными методами: |
|
|
|
|||||
Рис. 9.1а: По закону Гука при осевой нагрузке |
|
|
|
|||||
|
|
|
Dcт = Dl = Pl / EA |
|
|
|
||
Рис. 9.1б: |
Dcт = Vк - прогиб балки в т. K от силы P , приложенной в т. K. |
|||||||
Определяется известным методом Клебша из раздела «Плоский изгиб балок».
Скорость груза, падающего с высоты h , |
как известно, |
определяется |
||||||||
так V = |
|
, откуда 2h =V 2 / g . Подставим это в (9.8) получим |
||||||||
2gh |
||||||||||
|
|
Kд =1+ |
|
|
|
|
|
|||
|
|
1+V 2 / gDcт |
(9.9) |
|||||||
Преобразуем 2h / Dcт так: |
|
P × h |
|
T0 |
|
|
||||
|
|
2h / Dcт = |
|
= |
|
(12) |
||||
|
|
1 |
|
|
||||||
|
|
|
|
Dcт P |
Uст |
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь: T0 = P × h - энергия падающего груза в момент начала удара;
131
Ucт = 12 P × Dcт - потенциальная энергия деформации бруса от статического
нагружения его силой P в т. K. С учетом (12) из (9.8) найдем
Kд =1+ |
1+ T0 /Ucт |
|
(9.10) |
Из (9.8) следует, что чем больше |
cт , т.е. чем больше деформируется |
||
брус от статической нагрузки P , тем меньше Kд и по (9.6) меньше |
|||
напряжения при ударе. Так появилась идея ставить в конструкциях, испытывающих ударные нагрузки, различные амортизаторы, рессоры, пружины и поясняется поговорка «знал бы, где упаду, подстелил бы солому».
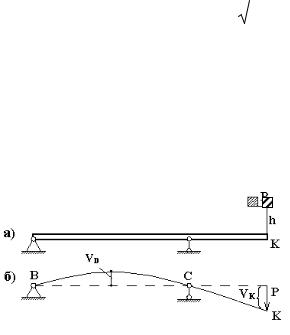
Пример. Порядок расчета балки на удар. |
|
|||
|
|
|
На балку с высоты h |
в т. K |
|
|
P |
||
|
|
|||
|
|
|
падает груз P . Найти |
σ дmax - |
максимальное напряжение в балке от удара, максимальные прогибы в пролете и консоли.
В т. K балки статически при-
кладываем силу P , равную весу груза (рис.б). Определяем от нее опорные реакции и строим эпюру M x− изгибающих моментов. Из Эп. M x находим
M xmax и, зная размеры и форму поперечного сечения балки, вычисляем
σ max =| M max | /W - |
максимальные напряжения от статического |
||
ст |
x |
x |
|
нагружения. Для вычислений по (9.6) надо знать Kд .
Для балки б) со статической силой P для двух участков запишем дифференциальные уравнения изгиба EJ xV ′′ = −M x по методу Клебша,
интегрируем их и из условий закрепления балки находим константы интегрирования. Строим график прогибов балки, приблизительный вид которого показан на рис.б. Находим Vк − прогиб балки в сечении «K», это
и есть cт = Vк . По (9.8) вычисляем Kд и далее
σдmax =σстmax × Kд
Вконсоли максимальный прогиб при ударе Vдmaxконс = Vк × Kд .
Впролете находим VD − максимальный прогиб от статического
нагружения и далее максимальный прогиб при ударе Vдmaxпролета =VD × Kд .
Дальше можно проверить балку на прочность и жесткость обычными методами.
Существует термин «падение с высоты h = 0 ». Из (9.8) в этом случае получим Kд = 2 . Чтобы этого не было, груз надо опускать плавно не
только до соприкосновения с конструкцией, но и дальше, при
132

перемещении груза вместе с деформируемой конструкцией до полной их остановки.
Учет массы ударяемого тела (бруса)
Учет массы ударяемого тела достаточно сложен, поэтому приведем окончательные формулы без вывода их.
Динамический коэффициент в этом случае определяется по формулам,
аналогичным (9.8)-(9.10)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
д |
=1+ |
|
1+ 2h /αD |
cт |
=1+ 1+V 2 /αgD |
cт |
=1+ |
|
1+T /αU |
cт |
(9.11) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||||||
Здесь: α = 1+ βQ / P ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Q − вес ударяемого тела, для бруса Q = γAl |
|
|
|
|
|
|
|
|
|
||||||||||||
β − редукционный коэффициент, определяется так |
|
|
|
||||||||||||||||||
|
|
|
1 |
|
æ |
Dст |
ö2 |
|
|
|
1 l |
æ |
Dст ö2 |
|
|
|
|||||
β = |
|
|
ç |
z |
÷ |
|
для бруса β = |
|
ò |
ç |
z |
÷ |
dz |
|
(9.12) |
||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
òç |
|
÷ dQ , |
|
ç |
÷ |
|
|
||||||||||||
|
|
|
Q Qè Dст |
ø |
|
|
|
l |
0 |
è Dст ø |
|
|
|
||||||||
Вычислив β , определяем коэффициент α и далее Kд .
Пример 1. Вычислить β для колонны, показанной на рис. 9.1а. По закону
Гука для сечения |
z от статического нагружения силой |
P : |
Dстz = Pz / EA, |
|||||||||||||||||||
cт = l = Pl / EA, |
где A − |
площадь поперечного сечения колонны, E − |
||||||||||||||||||||
модуль упругости материала. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 l |
æ |
Dст ö2 |
1 l |
æ |
PzEA ö2 |
1 l |
2 |
|
z3 |
|
l |
1 |
|
||||||||
|
|
|
|
|||||||||||||||||||
β = |
|
|
ç |
z |
÷ |
|
|
|
|
÷ dz = |
|
|
ò z |
dz = |
|
|
|
= |
|
|
. |
|
l |
ò |
ç |
|
÷ dz = |
ò |
ç |
|
l |
3 |
|
3l |
3 |
|
3 |
||||||||
|
0 |
è Dст ø |
l 0 |
è |
EA× Pl ø |
|
0 |
|
|
|
|
0 |
|
|||||||||
Пример 2. Вычислить β для балки, показанной на рис. 9.1б, когда груз P падает на середину балки.
Опорные реакции R = P / 2 , дифференциальные уравнения изгиба балки от статического нагружения силой P :
EJxV ¢¢ = -Rz, EJxV¢ = -Rz2 / 2 + C, EJxV = -Rz3 / 6 + C × z + D, 0 £ z £ l / 2 ,
т.е. ввиду симметрии ограничимся одним участком.
Граничные условия: 1) z = 0, V = 0 ; 2) z = l / 2, V ′ = 0 (ввиду симметрии),
откуда найдем
R = P / 2 , то EJxV
D = 0, C = Rl2 /8.
|
P |
æ |
z |
3 |
|
l |
2 |
ö |
, а V |
= - |
ç |
|
- |
|
z ÷ |
||||
|
|
|
|
|
|||||
4 |
ç |
3 |
4 |
÷ |
|
||||
è |
ø |
|
|||||||
Тогда |
EJ V = -Rz3 / 6 + Rl2z / 8, т.к. |
|||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
P |
æ |
z |
3 |
|
l |
2 |
ö |
, |
|
= Dст = - |
|
ç |
|
- |
|
z ÷ |
||||
|
|
|
|
|
|
|||||
z |
|
ç |
3 |
4 |
÷ |
|
||||
|
4EJx è |
ø |
|
|||||||
подставим z = l / 2 получим |
|
|
cт : |
|
|
|
|
|
|
Dст ö2 |
|
|
|
||||||
|
Pl3 |
|
Dст |
|
z3 |
|
z |
|
|
1 l æ |
|
17 |
|
||||||
Dcт = |
|
; Найдем |
|
z |
= -4 |
|
|
+ 3 |
|
: |
β = |
|
ò |
ç |
z |
÷ |
dz = |
|
. |
|
|
|
|
|
|
|
|
||||||||||||
48EJx |
D |
|
l |
3 |
l |
l |
ç |
÷ |
35 |
||||||||||
|
|
ст |
|
|
|
|
|
0 |
è Dст ø |
|
|
||||||||
Все полученные выше формулы приближенные. Чем большей жесткостью обладает ударяемый брус, тем менее точными будут результаты расчетов. Более точные результаты получаются при рассмотрении волновой теории удара.
133

III. Колебания тел
Колебания различных конструкций возникают обычно при действии на них знакопеременных нагрузок. Любая упругая конструкция имеет собственную частоту колебаний, определяемую ее жесткостью, массой, размерами, конструктивными особенностями и т.д. Определение собственных частот реальных конструкций – сложная задача. Для приближенных расчетов реальную конструкцию с нагрузкой (балку) заменяют системой грузов, установленных на невесомой балке (рис. 9.2б), т.е. масса балки сосредоточена в грузах. Число грузов определяет, сколько степеней свободы имеет система, заменяющая балку.
|
Наиболее простое |
решение |
|||
|
можно получить, когда балка |
||||
|
заменяется системой с одним грузом |
||||
|
(рис. 9.2а). |
|
|
|
|
|
Период |
свободных |
колебаний, |
||
|
т.е. время, за которое система |
||||
|
совершает |
одно |
свободное |
||
Рис.9.2 |
колебание: |
|
|
|
|
T = 2π |
|
[сек] |
|
|
|
Pδ / g |
|
|
|
||
Здесь: P − вес груза, δ − прогиб |
балки под |
грузом от силы |
F = 1, |
||
g = 9,81м/сек2. |
|
|
|
|
|
Более точно собственную частоту колебаний реальной балки |
можно |
||||
установить экспериментально. На балку крепится вибратор, конструкция
|
которого показана на рис: в корпусе установлены |
|
два вала с зубчатыми шестернями (пунктир) и |
|
двумя грузами (заштрихованы). Один вал с |
|
помощью гибкого шланга вращается электромото- |
вибратор |
ром постоянного тока (можно плавно изменять |
|
частоту вращения). Грузы при вращении создают знакопеременные инерционные центробежные силы в вертикальной плоскости, которые действуют на балку. Изменяя частоту вращения валов определяют частоту, при которой резко возрастает амплитуда колебаний балки с вибратором. Это и будет собственная частота колебаний балки, т.к. масса вибратора много меньше массы балки. Здесь учитываются все особенности реальной конструкции балки.
Этот способ основан на явлении резонанса при колебаниях. Резонанс возникает, когда частота внешних силовых импульсов приближается к частоте собственных колебаний конструкции. Явление резонанса играет большую роль в технике. При резонансе резко возрастает амплитуда колебаний конструкции (т.е. деформации и напряжения в ней), что часто приводит к разрушению конструкций. Примерами резонансных колебаний являются: автоколебания подвесных мостов, флаттер частей самолетов (крыльев, хвостового оперения), колебания высотных зданий и
134

сооружений (в них ставят специальные гасители колебаний) и др. В уставе армии есть пункт – в начале движения солдат по любому мосту должна следовать команда «сбить шаг». В истории известен случай, когда частота шагов солдат на мосту оказалась близка к собственной частоте колебаний моста, он вошел в резонанс и разрушился.
Внешние знакопеременные нагрузки могут передаваться на конструкции от различных механизмов, станков и т.д., установленных на них. Конструкции, на которых они установлены, должны иметь собственные частоты колебаний далекие от частот внешних воздействий. Резонанс в большинстве конструкций нельзя допускать, это может привести к их разрушению.
Многочисленные опыты показали, что при действии переменных напряжений, возникающих при колебаниях конструкций, разрушение происходит при напряжениях значительно меньших, чем опасные напряжения при однократном статическом нагружении. Причиной разрушения материала при колебаниях является постепенное развитие микротрещин, которые всегда есть в материале. Это явление называется усталостью материала. Способность материала воспринимать многократное действие переменных напряжений называют выносливостью, а проверку прочности элементов конструкций при действии таких напряжений – расчетом на выносливость (или расчетом на усталостную прочность).
Для расчетов на выносливость используют кривые усталости или кривые Вёлера, которые экспериментально получаются для каждого
материала. На рис. показана примерная кривая Вёлера. |
|
|
||||
|
|
|
|
По вертикальной оси отклады- |
||
|
|
|
ваются максимальные |
напряжения, |
||
|
|
|
возникающие |
при |
колебании |
|
|
|
|
конструкции, а по горизонтальной |
|||
|
|
|
оси |
N − число циклов нагружения |
||
|
|
|
до |
разрушения |
материала. Видно, |
|
|
σR |
|||||
|
|
|
что чем меньше σmax , тем больше |
|||
|
|
|
||||
Кривая Вёлера |
циклов выдержит материал. Для |
|||||
стали кривая стремится к асимптоте при σmax = σ R , |
которую называют |
|||||
пределом выносливости. Это напряжение, при котором не происходит усталостного разрушения данного материала после произвольно большого
числа циклов (обычно берут N = 107 циклов).
С помощью кривых Вёлера определяют срок службы элементов конструкций при действии переменных напряжений, возникающих при колебаниях.
На величину предела выносливости влияют многие факторы: Концентрация напряжений. Она возникает в точках тела вблизи мест
приложения сосредоточенных сил, около выточек, у краев отверстий, в
135
местах резкого изменения формы тела, у надрезов и т.д. Концентрация значительно снижает предел выносливости.
Качество поверхности детали. Снижение предела выносливости тем больше, чем грубее поверхностная обработка детали, причем это снижение более значительно для материалов с высокими пределами прочности.
Абсолютные размеры детали. С увеличением размеров предел выносливости уменьшается. Объясняют это тем, что в больших деталях с большим объемом материала больше дефектных мест (раковины, микротрещины, неметаллические включения, следы от обработки поверхности).
Внешняя среда. Коррозионная среда (вода, соленая вода, кислоты, пары и т.д.) резко снижают усталостную прочность. Желательно использовать защитные покрытия поверхностей (окраска, цинкование, азотирование и т.д.)
136

РАЗДЕЛ 10 БАЛКА НА УПРУГОМ ОСНОВАНИИ
В инженерной практике встречаются балки, лежащие на сплошном упругом основании. Это ленточные фундаменты зданий, фундаменты плотин, ж/д шпалы и др. Расчет таких балок осложняется
Рис.10.1 тем, что реакция оснований « r » зависит от прогибов «V » балки, а прогибы зависят от реакции основания. Для решения задачи необходимо знать закон, связывающий реакцию основания с осадкой (прогибом) основания. Наиболее распространенной является гипотеза Винклера
Обозначим |
r = −kV |
(1) |
||
q = r + p = −kV + p |
(2) |
|||
|
||||
Здесь: p − |
внешняя погонная |
нагрузка; |
k − коэффициент постели, |
|
приводится |
в справочниках для |
различных грунтов; q − суммарная |
||
погонная нагрузка, действующая на балку.
Для решения задачи используем известное дифференциальное уравнение изогнутой оси бруса
|
EJ xV ′′ = −M x |
|
|
(3) |
||
Обычно EJ x − изгибная жесткость балки, |
считается константой. |
Ранее |
||||
получены дифференциальные зависимости (1.7) |
|
|
||||
|
dM |
x |
= Qy , |
dQy |
= −q |
(4) |
|
dz |
|
dz |
|||
|
|
|
|
|
||
Дифференцируя один раз (3) с учетом (4) получим |
|
|||||
EJxV′′′ = −Qy |
|
|
(5) |
|||
Дифференцируя (5) с учетом (4) найдем |
|
|
|
|||
EJ V IV = q |
|
|
(6) |
|||
|
x |
|
|
|
|
|
Подставим (2) в (6) |
|
|
|
|
|
|
EJ V IV = −kV + p |
|
(7) |
||||
|
x |
|
|
|
|
|
Обозначим 4α 4 = k / EJx |
|
|
|
|
|
|
Тогда уравнение (7) примет вид |
|
|
|
|
|
|
V IV + 4α 4V = p / EJx |
|
(10.1) |
||||
Это дифференциальное уравнение балки на упругом основании.
137

I. Бесконечно-длинная балка, загруженная локальной силой
Задача симметрична относительно силы F , поэтому рассмотрим лишь ее правую половину. Начало координат
поместим под силой |
F . Здесь |
p = 0 |
и |
|
уравнение (10.1) примет вид |
|
|
||
Рис.10.2 |
V IV + 4α 4V = 0 |
(9) |
||
|
|
|
|
|
Общий интеграл этого уравнения приводится в справочниках |
|
|
||
V = Aeαz sin αz + Beαz cosαz + Ce−αz sin αz + De−αz cosαz |
(10.2) |
|||
Здесь: A, B, C, D − неизвестные |
const, которые |
определяются |
из |
|
граничных условий задачи: |
|
|
|
|
1. При z = ∞ V = 0. Подставим это в (10.2) |
|
|
|
|
0 = A∞sin ∞ + B∞cos∞ + C / ∞ + D / ∞ |
|
|
|
|
Это может быть, когда A = B = 0. |
Уравнение (10.2) с учетом этого |
|||
упростится |
|
|
|
|
V = Ce−αz sinαz + De−αz cosαz |
|
(10.3) |
||
2. Ввиду симметрии прогибов: при |
z = 0 V ′ = 0. Дифференцируем (10.3), |
|||
получим |
|
|
|
|
V ′ = C(−αe−αz sinαz + αe−αz cosαz) + D(−αe−αz cosαz −αe−αz sinαz) |
|
|||
Подставляем z = 0 и V ′ = 0 найдем |
|
|
|
|
0 = C(0 + α) + D(−α − 0) = Cα − Dα = α(C − D) = 0 |
|
|
||
Отсюда следует, что C = D и уравнение (10.3) еще упростится |
|
|
||
V = Ce−αz (sinαz + cosαz) |
|
(10) |
||
3. Правило проверки эпюр Qy гласит: при движении вдоль эпюры Qy
справа – налево скачки на эпюре должны равняться по величине и по направлению локальным силам, приложенным в этих сечениях балки. В нашем случае Эп. Qy в окрестности силы F с учетом симметрии задачи
должна иметь вид (рис. 10.3):
Отсюда при z = 0 Qy = −F / 2 . Подставим это в (5), получим
EJ xV ′′′ = F / 2 при z = 0 |
(11) |
Надо найти V ′′′ от (10) |
последовательным |
дифференцированием |
|
Рис.10.3 |
|
V ′ = −Cαe−αz (sinαz + cosαz) + Cαe−αz (cosαz − sinαz) |
|
V ′ = −2Cαe−αz sinαz |
|
V ′′ = −2Cα (−αe−αz sinαz + αe−αz cosαz) |
|
V ′′ = −2Cα 2e−αz (cosαz − sinαz) |
(12) |
138

V ′′′ = −2Cα 3(−e−αz (cosαz − sinαz) − e−αz (sinαz + cosαz)) |
|
|||||||||||||
|
|
|
V ′′′ = 4Cα 3e−αz cosαz |
(13) |
||||||||||
Подставим (13) в (11) найдем |
|
|
|
|
|
|
|
|
|
|||||
откуда |
|
|
EJx 4Cα3 = F / 2 , |
|
||||||||||
|
|
|
C = F / 8α 3EJx |
|
||||||||||
|
|
|
|
(14) |
||||||||||
Подставим (14) в (10), получим прогибы балки |
|
|||||||||||||
|
V = |
|
F |
|
|
|
e−αz (sinαz + cosαz) |
(10.4) |
||||||
Подставим V ′′ |
8α 3EJ x |
|||||||||||||
|
|
|
|
|
|
|
||||||||
по (12) и С по (14) в (3), получим формулу для изгибающих |
||||||||||||||
моментов в балке |
|
F |
|
|
|
|
|
|
|
|
|
|
||
|
M x = |
e |
−αz |
(cosαz − sinαz) |
(10.5) |
|||||||||
Подставим V ′′′ |
4α |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
из (13) и С по (14) в (5), получим формулу для поперечных |
||||||||||||||
сил в балке |
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
Qy |
= − |
|
e |
−αz |
cosαz |
(10.6) |
|||||
|
|
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
По формулам (10.4)-(10.6) можно построить эпюры, примерный вид которых показан ниже.
Рис.10.4 |
|
Эпюры V и M x симметричны относительно т.О, |
а эпюра |
Qy − обратносимметрична. Эпюры представляют собой |
затухающие |
функции с увеличением z . |
|
Обозначим l0 = π /α - длина полуволны. Расчеты показали, что при z = 2l0
V ≈ 0,2% от прогиба под силой F (Vmax ) , при z = l0 V ≈ 4% от Vmax . Поэтому, полученными формулами можно пользоваться и для балок конечной длины, если их длина l ³ 4l0 и даже при l ³ 2l0 . Для более
коротких балок ошибки будут значительны.
139

II. Полубесконечная балка на упругом основании
Балка загружена при z = 0 Q0
|
и M0 . |
Здесь p = 0 и для решения |
|
|
задачи |
можно |
использовать |
|
уравнение (9), |
общее решение |
|
Рис.10.5 |
которого дано (10.2). |
||
|
A = B = 0, |
|
|
Граничное условие: при z = ∞ V = 0 дает |
что приводит к |
||
уравнению (10.3) |
|
|
|
V = Ce−αz sinαz + De−αz cosαz
Для определения const С и D есть два граничных условия
1. |
при z = 0 M x = M0 ; с учетом (3) EJ xV ′′ = −M0 |
2. |
при z = 0 Qy = Q0 ; с учетом (5) EJ xV ′′′ = −Q0 |
Последовательным дифференцированием (15) найдем
(15)
(16)
(17)
V ′ = α(C − D)e−αz cosαz −α(C + D)e−αz sinαz |
(18) |
||||||||||
V ′′ = 2α 2e−αz (Dsinαz − C cosαz) |
|
(19) |
|||||||||
V ′′′ = 2α 3e−αz ((D + C)cosαz − (D − C)sinαz) |
(20) |
||||||||||
Подставим V ′′ из (19) при z = 0 в (16) получим |
|
||||||||||
|
|
|
|
C = M0 / 2α 2EJx |
|
|
(21) |
||||
Подставим V′′′ по (20) при z = 0 в (17) найдем |
|
||||||||||
|
D = −(Q +αM |
0 |
) / 2α 3EJ |
x |
(22) |
||||||
Подставляя в (3) V ′′ |
|
|
0 |
|
|
|
|||||
из (19) и найденные значения С и D из (21)-(22), после |
|||||||||||
преобразований получим |
|
|
|
|
|
|
|
||||
M |
x |
= |
e−αz |
|
(Q sinαz + αM |
0 |
(cosαz + sinαz)) |
(10.7) |
|||
|
|
||||||||||
|
|
|
α |
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Подстановка V′′′ по (20), С и D в (5) дает |
|
|
|
||||||||
Q |
y |
= −e−αz (Q (sinαz − cosαz) + 2M α sinαz) |
(10.8) |
||||||||
|
|
|
0 |
|
|
|
0 |
|
|||
В формулы (10.7) и (10.8) Q0 |
и M0 подставлять со своими |
знаками, |
|||||||||
положительные их направления на левом торце балки показаны на рис. 10.5.
a
a Q y а
M x
M0a 
 Q 0a
Q 0a
III. Расчет короткой балки методом |
|
|
|||
последовательных приближений |
|
|
|||
|
b |
Рассмотрим |
короткую |
балку |
|
b |
M x |
a − b , загруженную силой F , под |
|||
b |
|
которой поместим начало координат |
|||
|
(рис.10.6). Представим ее беско- |
||||
Q y |
|
||||
|
b |
нечно длинной в |
оба конца |
и по |
|
Q |
формулам (10.5) и (10.6) построим |
||||
0 |
|||||
|
b |
эпюры Qy и M x |
на участке |
a − b . |
|
|
M 0 |
Пусть в сечениях «а» и «b» эти |
|||
Рис.10.6 |
|
внутренние силовые факторы (ВСФ) |
|||
140
