ЧМ-1

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

Кафедра прикладной математики

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по курсу "Информатика"

для самостоятельной работы студентов всех специальностей

ЧИСЛЕННЫЕ МЕТОДЫ

ЧАСТЬ 1

Казань

2008

2

Составители: Ф.Г.Ахмадиев, Ф.Г.Габбасов, И.Н.Гатауллин, Р.Ф.Гиззятов, Р.И.Ибятов, Х.Г.Киямов.

УДК 621.313: 518.6

Методические указания по курсу "Информатика" для самостоятельной работы студентов всех специальностей. Численные методы. Часть 1. /Казанский государственный архитектурно-строительный университет. Сост.: Ф.Г.Ахмадиев, Ф.Г.Габбасов, И.Н.Гатауллин, Р.Ф.Гиззятов, Р.И.Ибятов, Х.Г.Киямов. Казань, 2008. -35 с.

Методические указания состоят из двух частей и предназначены для самостоятельной работы студентов всех специальностей 2-го курса дневного и заочного отделений. В данной работе приводятся численные методы решения нелинейных уравнений, систем линейных и нелинейных алгебраических уравнений, дифференциальных уравнений, определенных интегралов, методы аппроксимации дискретных функций и методы решения задач линейного программирования.

Табл. 8, библиогр. назв. 6.

Рецензент - Р.Б.Салимов, доктор физ.-мат. наук, профессор

Казанский государственный

архитектурно-строительный университет, 2008г.

3

1. Численное решение нелинейных уравнений.

Задана непрерывная функция F(x). Требуется определить корни урав-

нения F(x)=0.

Такая задача встречается в различных областях научных исследований, в том числе и при расчетах строительных конструкций, организации и управлении строительным производством.

Нелинейные уравнения можно разделить на два класса - алгебраические и трансцендентные. Алгебраическими уравнениями называются уравнения, содержащие только алгебраические функции.

Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и др.) называются трансцендентными.

Методы решения нелинейных уравнений делятся на прямые и итерационные. Прямые методы позволяют записать корни в виде некоторого конечного соотношения. Если не удается решить уравнения прямыми методами, то для их решения используются итерационные методы, т.е. методы последовательных приближений. Алгоритм нахождения корня уравнения с помощью итерационного метода состоит из двух этапов:

а) отыскания приближенного значения корня, или содержащего его от-

резка;

б) уточнения значения до некоторой степени точности. Приближенное значение корня (начальное приближение) может быть

найдено различными способами из физических соображений, из решения аналогичной задачи при других исходных данных, с помощью графических методов. Если такие простые оценки исходного приближения произвести не удается, то находят две близко расположенные точки a и b, в которых непрерывная функция F(x) принимает значения разных знаков, т.е. F(a)•F(b)<0 . В этом случае между точками a и b есть, по крайней мере, одна точка, в которой F(x)=0. В качестве начального приближения первой итерации x0 можно принять середину отрезка [a, b], т.е. x0=(a+ b)/2.

Итерационный процесс состоит в последовательном уточнении x0. Каждый такой шаг называется итерацией. В результате итераций находятся последовательности приближенных значений корня x0, x1, ... , xn. Если эта последовательность с ростом значения n приближается к истинному значению корня, то итерационный процесс сходится.

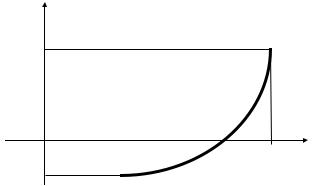
1.1. Метод деления отрезка пополам.

Допустим, что мы нашли отрезок [a, b], в котором расположено искомое значение корня x = c, т.е. a<c<b.

4

Пусть для определенности F(a)<0, F(b)>0 (см. рис. 1.1). В качестве начального приближения корня x0 принимается середина этого отрезка, т.е. x0 = (a + b)/2. Далее исследуем значение функции F(x) на концах отрезков [a,x0] и [x0,b]. Тот из них, на концах которого F(x) принимает значения разных знаков, содержит искомый корень. Поэтому его принимаем в качестве нового отрезка. Вторую половину отрезка [a, b] отбрасываем. В качестве первой итерации корня принимаем середину нового отрезка и т. д.

y

y=F(x)

F(b)

Поскольку в рассматриваемом случае F(x0)<0, то x0<c<b, и рассматриваем отрезок [x0,b]. Следующее приближение: x1=(x0+b)/2 и т.д. Итерационный процесс продолжаем до тех пор, пока значение функции F(x) после n-й итерации не станет меньшим по модулю некоторого заданного малого числа e, т.е. |F(xn)|<e. Можно также оценивать длину полученного отрезка, если она становится меньше допустимой погрешности, то счет прекращается.

Пример: Найти решение уравнения x3+x-1=0 c точностью e=0.01 методом деления отрезка пополам.

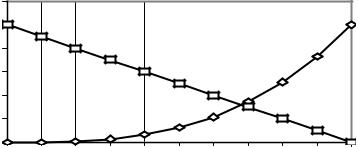
Решение: Данное уравнение представим в виде x3=-x+1. Корнем данного уравнения является точка пересечения графиков функций y=x3 и y=- x+1 (рис.1.2). Искомый корень находится между точками a=0 и b=1. Функция F(x)=x3+x-1 на концах отрезка [0,1] принимает значения разных знаков

F(a)×F(b)<0.

В точках 0; 0.5; 1 заданная функция принимает значения -1; -0,375 и 1, следовательно, корень находится в интервале [0,5;1] (т.е. на концах этого интервала F(x) принимает значения разных знаков). Далее в точках 0,5;

|xi+1-xi|=|0,6875-0,679688|=0,007812<0.01

и оформляются в виде таблицы 1.1. Приближенным решением данного уравнения является x=0,683594.

На рис. 1.3 приведена программа решения данного уравнения методом деления отрезка пополам.

6

CLS

REM LR-1-1, m=13, n=5

DEF FNF(X) = X^3+X-1

1INPUT A, B, E

YA= FNF(A): YB=FNF(B) IF YA*YB>0 THEN 1

2X =(A+B)/2: Y=FNF(X) PRINT X, Y

IF YA*Y<0 THEN B=X ELSE A=X IF (B-A)>E THEN 2

END

Рис.1.3. Пример программы нахождения корней уравнения методом деления отрезка пополам.

1.2. Метод Ньютона (метод касательных).

Суть метода состоит в том, что на k-й итерации в точке (xk, F(xk)) строится касательная к кривой y=F(x) и ищется точка пересечения касательной с осью абсцисс. При этом необязательно задавать отрезок [a, b], содержащий корень уравнения, а достаточно найти лишь некоторое начальное приближение корня x=x0 (рис. 1.4). Если задан интервал изоляции корня [a,b], то за начальное приближение x0 принимается тот конец отрезка, на котором

F(x0)·F²(x0)> 0.

Уравнение касательной, проведенной к кривой y=F(x) в точке M0 с координатами x0 и F(x0), имеет вид:

Рис. 1.4. Метод касательных.

7

За следующее приближение корня x1 примем абсциссу точки пересечения касательной с ocью оx:

При этом необходимо, чтобы F¢(x0) не равнялся нулю:

F¢(x0)¹0

Аналогично могут быть найдены и следующие приближения, как точки пересечения с осью абсцисс касательных, проведенных в точках M1, M2 и т.д. Формула для n+1-го приближения имеет вид:

Для завершения итерационного процесса можно использовать условие ½F(xn)½< e, или условие близости двух последних приближений: ½xn+1-xn½<e.

Объем вычислений в методе Ньютона больше, чем в других методах, поскольку приходится находить значение не только функции F(x), но и ее производной. Однако скорость сходимости здесь значительно выше.

Пример: Решить уравнение F(x)=x3+x-1=0 на отрезке [0;1] методом Ньютона c точностью e=0.01.

Решение: Определим первые и вторые производные заданной функции: F¢(x)=3x2+1; F²(x)=6x. Вычислим значения функции F(x) на концах заданного интервала F(0)=-1; F(1)=1. Так как F(1)·F²(1)=1·6>0, за начальное приближение корня можно принять x=1. Находим первое приближение:

x1=x0-F(x0)/F¢(x0)=x0-(x03+x0-1)/(3x02+1)=1-(13+1-1)/(3·12+1)=0,75

Аналогично находится второе приближение:

x2=x1 - F(x1)/F¢(x1)=x1-(x13+x1-1)/(3x12+1)=

=0,75-(0,753+0,75-1)/(3·0,752+1)=0,686047

Аналогично находится третье приближение:

x3 =x2 - F(x2)/F¢(x2)=x2-(x23+x2-1)/(3x22+1)=

8

=0,686047-(0,6860473+0,686047-1)/(3·0,6860472+1)=0,68234

Так как ½x3 - x2½=½0,68234-0,686047½=0,00371< 0.01, итерационный процесс заканчивается. Таким образом, приближенным решением данного уравнения является x = 0,68234.

На рис. 1.5 приведена программа решения данного уравнения методом Ньютона.

CLS

REM LR-1-2, m=13, n=5

DEF FNF(X)=X^3+X-1

DEF FNP(X)=3*X+1

INPUT X, E

1X=X- FNF(X)/FNP(X) PRINT X, FNF(X)

IF ABS(FNF(X)/FNP(X))>E THEN 1 END

Рис. 1.5. Программа нахождения корней методом Ньютона.

1.3. Метод простой итерации.

Для использования этого метода исходное нелинейное уравнение F(x)=0 необходимо привести к виду x = j(x).

В качестве j(x) можно принять функцию j(x) =x-F(x)/M, где M неизвестная постоянная величина, которая определяется из условия сходимости метода простой итерации |j¢(x)|<1. При этом для определения M условие сходимости записывается в следующем виде:

½1-F’(x0)/M ½<1 или M=1.01· F’(x0).

Если известно начальное приближение корня x=x0, подставляя это значение в правую часть уравнения x=j(x), получаем новое приближение

x1=j(x0).

Далее подставляя каждый раз новое значение корня в уравнение x=j(x), получаем последовательность значений:

x2=j(x1), x3=j(x2),..., xk+1=j (xk)..... k = 1,2,...,n.

9

Итерационный процесс прекращается, если результаты двух последовательных итераций близки, т.е. ½xk+1 - xk½< e.

Пример: Решить уравнение F(x)=x3+x-1=0 на отрезке [0;1] методом простой итерации c точностью e=0.01.

Решение: Из условия сходимости

½1-F¢(x0)/M½<1 или ½1-(3x0+1)/M½<1,

при x0=1 определяем M>4. Пусть M = 5.

Подставляя каждый раз новое значение корня в уравнение

xk+1=xk-(xk3+x-1)/5,

получаем последовательность значений:

x1=x0-(x03+x0-1)/5=1 - (13+1-1) / 5 = 0,8

x2 = x1-(x13+x1-1)/5=0,8 - (0,83+0,8 -1) / 5 = 0,7376

x3 =x2-(x23+x2-1)/5=0,7376 - (0,73763+0,7376 -1) / 5 = 0,709821

x4 =x3 -(x33+x3-1)/5=0,709821- (0,7098213+0,709821-1) / 5 = 0,696329

x5=x4-(x43+x4-1)/5=0,696329- (0,6963293+0,696329-1) / 5 = 0,689537

½x5 - x4½ = ½0,689537- 0,696329½ = 0,00679 < 0.01.

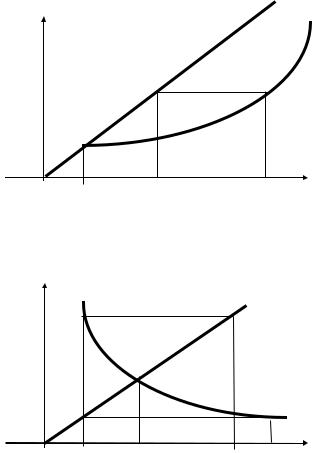
Геометрическая интерпретация метода простой итерации.

Построим графики функций y=x и y=j(x). Корнем x* уравнения x=j(x) является абсцисса пересечения кривой y=j(x) с прямой y=x ( см. рис. 1.6). Взяв, в качестве начальной точки точку x0 строим, ломаную линию. Абсциссы вершин этой ломаной представляют собой последовательные приближения корня x*. Из рисунка видно, что если -1<j¢(x)<0 на отрезке [a, b] (рис. 1.6b), то последовательные приближения xi+1 = j(xi) колебаются около корня. Если же производная 0<j¢(x)<1 (рис. 1.6.а), то последовательные приближения сходятся монотонно.

10

На рис.1.7 приведена программа решения данного уравнения методом простой итерации.

y =x

a) y

y=ϕ (x)

y=ϕ(x)

Рис.1.6. Геометрическая интерпретация метода простой итерации.

CLS

REM LR-1-3, m=13, n=5

DEF FNF(X)= X^3+X-1

INPUT X, E, M

1X = X - FNF(X)/M PRINT X, FNF(X)

IF ABS(FNF(X)/M)>E THEN 1 END

Рис.1.7. Программа решения уравнения методом простой итерации.