
ЧМ-2
.pdfКАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
Кафедра прикладной математики
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по курсу "Информатика"
для самостоятельной работы студентов всех специальностей
ЧИСЛЕННЫЕ МЕТОДЫ
ЧАСТЬ 2
Казань
2008
2
Составители: Ф.Г.Ахмадиев, Ф.Г.Габбасов, И.Н.Гатауллин, Р.Ф.Гиззятов, Р.И.Ибятов, Х.Г.Киямов.
УДК 621.313: 518.6
Методические указания по курсу "Информатика" для самостоятельной работы студентов всех специальностей. Численные методы. Часть 2. /Казанский государственный архитектурно-строительный университет. Сост.: Ф.Г.Ахмадиев, Ф.Г.Габбасов, И.Н.Гатауллин, Р.Ф.Гиззятов, Р.И.Ибятов, Х.Г.Киямов. -Казань, 2008. -35с.
Методические указания состоят из двух частей и предназначены для самостоятельной работы студентов всех специальностей 2-го курса дневного и заочного отделений. В данной работе приводятся численные методы решения нелинейных уравнений, систем линейных и нелинейных алгебраических уравнений, дифференциальных уравнений, определенных интегралов, методы аппроксимации дискретных функций и методы решения задач линейного программирования.
Табл. 6, библиогр. назв. 6.
Рецензент - Р.Б.Салимов, доктор физ.-мат. наук, профессор
Казанский государственный
архитектурно-строительный университет, 2008г.
3
5. Численное интегрирование.
Требуется вычислить определенный интеграл:
b |
|
I= ∫ f ( x)dx |
(5.1) |
a |
|
Выберем на отрезке интегрирования [а,b] n различных узлов |
|
a=x0<x1<x2<... |
xn-1< xn = b |
и интерполируем функцию f(x) по ее значениям в этих узлах некоторым полиномом Pm(x).
Тогда определенный интеграл (5.1) приближенно можно вычислять по формуле
b |
|
Iʲ = ∫ Pm(x)dx , |
(5.2) |
a
которая называется квадратурной формулой интерполяционного типа.
5.1. Метод прямоугольников.
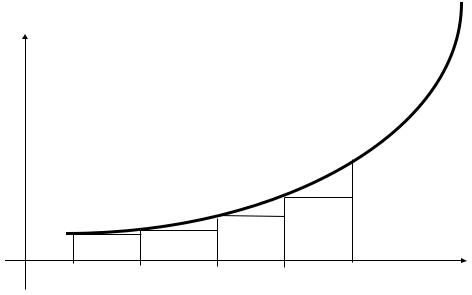
На каждом отрезке [xi, xi+1], i=0,1,2,...,n-1 функция f(x) заменяется полиномом нулевой степени P0(x)=f(xi).
Поэтому приближенно I вычисляется по формуле (см. рис. 5.1):
|
|
|
n−1 |
|
|
|
|
Iʲʲ = ∑ f(x i) (xi+1- x i). |
(5.3) |
||
|
|
|
i=0 |
|
|
Величина ошибки½Iʲ-I½ определяется |
ошибкой интерполирования |
||||
½f(x)-Pm(x)½ на отрезке [а,b] и может быть представлена в форме |
|||||
|
1 |
|
b |
|
|
R(f)= |
|
∫ (x-x1)(x-x2)...(x-xn)f(n)(x)dx, |
(5.4) |
||
n ! |
|||||
|
a |
|
|||
|
|
|
|
||
Нахождение точного значения R(f) затрудняет то обстоятельство, что не известна зависимость x от x. Однако, если известна производная порядка n, то ее всегда можно оценить
½ f(n)(x)½£ Mn , x Î [а,b]. |
|
(b-a)2 |
|
½I-Iʲ½£ ¾¾¾ M1, |
(5.5) |
2n |
|
4
где M1=max½f (x)½- наибольшее значение модуля первой производной f(x) на отрезке [a, b].
y
y=f(x)
f(x0) f(x1)
0 x0=a |
x1 |
x2 ... xn-1 xn=b |
x |
Рис. 5.1. Метод прямоугольников.
Для равноотстоящих узлов формула (5.5) имеет следующий вид:
|
|
n−1 |
|
|
Iʲ |
= h ∑ f(xi), h = xi+1- x i |
(5.6) |
|
|
i =0 |
|
|
|
n |
|
или |
Iʲ |
= h ∑ f(xi). |
(5.7) |
i=1
Формулу (5.6) называют формулой левых прямоугольников, а (5.7) правых прямоугольников.
Программа вычисления интеграла методом прямоугольников представлена на рис. 5.2.
REM LR-5-1, m=13, n=5
DEF FNF(X)=2*X^2+.1
DATA 0,1,8
READ A,B,N
H=(B-A)/N
S=0: X=A
1S=S +FNF(X)*H
X=X+H
IF X<B THEN 1 PRINT ²S=²; S END
Рис. 5.2. Программа вычисления интеграла методом прямоугольников.

5
5.2.Метод трапеций.
Вэтом методе на каждом отрезке [xi ,xi+1] функция f(x) заменяется полиномом 1-й степени P1(x).
По формуле Лагранжа:
P(x) = f (x } |
|
x−xi+1 |
+ f (x |
) |
x−xi |
. |
|
(5.9) |
|||||||
|
|
|
|
|
|||||||||||
1 |
i x −x |
i+1 |
|
x |
−x |
|
|||||||||
|
|
|
|
|
i |
i+1 |
|
|
i+1 |
i |
|
|
|||
Интегрируя P1(x) на отрезке [ xi ,xi+1], получим: |
|
||||||||||||||
Xi +1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
∫ P1(x)dx = |
|
(f(xi)+f(xi+1))(xi+1- xi) |
|
(5.10) |
|||||||||||
|
|
||||||||||||||
Xi |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
Суммируя по всем i |
(i = 0,1,...,n-1), |
получим формулу трапеций (см. |
|||||||||||||
рис. 5.3): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
n−1 |
|
|
|
|
|
|
|
||
Iʲ |
= |
∑ (f(xi)+f(xi+1))(xi+1-xi) |
(5.11) |
||||||||||||
|
|||||||||||||||
|
2 |
i =0 |
|
|
|
|
|
|
|
||||||
Для равноотстоящих узлов x0, x1=x0+h,...,xn=x0+nh |
формула (5.11) |
||||||||||||||
принимает следующий вид: |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
n−1 |
|
|
|
|
||
Iʲ = h [(f(x0)+f(xn))/2+ ∑ f(xi)] |
(5.12) |
|
|||||||||||||
i =1
y
f(x0)
f(x1)
y=f(x)
0 x0=a |
x1 |
x2 ... |
xn-1 xn=b |
|
Рис. 5.3. Метод трапеций. |
|
|||
Погрешность этого метода оценивается следующим выражением: |
||||
½I-Iʲ ½£ |
(b − a)3 |
M2 , |
|
(5.13) |
12n 2 |
|
|||
|
|
|
|
|
где M2=max½f²(x)½- наибольшее значение модуля второй производной f²(x) на отрезке [a,b].
6
Программа вычисления интеграла методом трапеций представлена на рис. 5.4.
REM LR-5-2, m=13, n=5
DEF FNF(X)=2*X^2+0.1
DATA 0,1,8
READ A,B,N
H=(B-A)/N
S=(FNF(A)+FNF(B))/2
X= A+H
1S=S+FNF(X)
X=X+H
IF X<B THEN 1
S=S*H PRINT ²S=²; S END
Рис. 5.4. Программа вычисления интеграла методом трапеций.
Метод парабол (Симпсона)
Интервал [a,b] разделим на 2n отрезков. Группируя узлы тройками
xi-1,xi,xi+1, на каждом отрезке [xi-1,xi+1] i=1,3,...,2n-1 интерполируем функцию f(x) полиномом 2-й степени P2(x):
По формуле Лагранжа:
|
|
|
|
(x − xi )(x − xi+1 ) |
(x − xi−1 )(x − xi+1 ) |
|
|
|||||||
P2(x)=f(xi-1) |
|
|
|
|
|
.+f(xi) |
|
|
. + |
|
||||
(xi−1 − xi )(xi−1 − xi+1 ) |
(xi − xi−1 )(xi − xi+1 ) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
+ f(xi+1) |
|
(x − xi−1 )(x − xi ) |
. . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
(xi+1 − xi−1 )(xi+1 − xi ) |
|||
Интегрируя P2(x) на отрезке [xi-1 ,xi+1], получим: |
|
|
||||||||||||
Xi +1 |
|
|
|
|
|
|
|
|
|
|
|
|||
∫ P2(x)dx = |
|
|
h |
[f(xi-1)+4f(xi)+f(xi+1)] . |
(5.14) |
|||||||||
3 |
||||||||||||||
Xi −1 |
|
|
|
|
|
|
|
|
||||||
Суммируя |
формулу (5.14) по всем n блокам, получаем формулу для |
|||||||||||||
приближенного интегрирования (см. рис.5.5): |
|
|
||||||||||||
n−1 |
|
|
|
|
|
|
|
|
|
|
|
|||
Iʲ = ∑ |
h |
[(f(x2k)+4f(x2k+1)+f(x2k+2)] |
|
|
(5.15) |
|||||||||
|
|
|
||||||||||||
k =0 3 |
|
|
|
|
|
|
|
|
|
|
|
|||
Погрешность метода Симпсона оценивается формулой: |
||||||||||||||
½I-Iʲ ½£ |
(b − a)5 |
M4 , |
|
|
(5.16) |
|||||||||
|
|
|
||||||||||||
|
|
|
|
180(2n) 4 |
|
|
|
|
||||||
7
где M4=max½fIV(x)½- наибольшее значение модуля четвертой производной fIV(x) на отрезке [a,b].
y
f(x0)
f(x1)
f(x2) y=f(x)
0 x0=a x1 |
x2 |
... |
x2n-1 x2n=b |
Рис. 5.3. Метод парабол (Симпсона).
Пример: Требуется вычислить определенный интеграл методами прямоугольников, трапеций и парабол:
1
I = ∫ (2x2+0,1) dx
0 |
|
Решение: Выберем на отрезке интегрирования [0,1] |
n=8 различных |
узлов |
|
0=x0<x1<x2<...x7< x8 =1 |
|
Шаг разбиения для равноотстоящих узлов h = xi+1-x i |
определяем по |
формуле |
|
h = (b-a)/n = (1-0)/8 =0,125 |
|
Тогда определенный интеграл приближенно можно вычислять по формуле левых прямоугольников
7
Iʲ = h ∑ (2xi2+0,1)
i=0
или по формуле правых прямоугольников
8
Iʲ = h ∑ (2xi2+0,1)
i=1
Определенный интеграл вычислим по формуле трапеций
7
Iʲ = h [(f(x0)+f(xn))/2+ ∑ f(xi)]
i=1
8
Определенный интеграл вычислим по формуле парабол
|
|
3 |
|
|
|
|
|
|
|
|
Iʲ = ∑ |
h |
[(f(x2k)+4f(x2k+1)+f(x2k+2)] |
|
|
|
|||
|
|
|
|
|
|||||
|
|
k =0 3 |
|
|
|
|
|
||
|
Результаты решения приводятся в таблице 5.3 |
|
|
||||||
|
|
|
|
|
|
|
|
Таблицы 5.3 |
|
|
|
|
|
|
|
|
|
||
i |
xi |
f(xi) |
h f(xi) |
Метод левых |
Метод правых |
Метод |
Метод |
||
|
|
|
|
|
|
прямоуголь- |
прямоуголь- |
трапеций |
парабол |
|
|
|
|
|
|
ников |
ников |
|
|
0 |
0 |
0,1 |
|
|
0,0125 |
0,0125 |
0 |
0,00625 |
0,004167 |
1 |
0,125 |
0,13125 |
0,016406 |
0,016406 |
0,016406 |
0,016406 |
0,021875 |
||
2 |
0,25 |
0,225 |
|
|
0,028125 |
0,028125 |
0,028125 |
0,028125 |
0,01875 |
3 |
0,375 |
0,38125 |
0,047656 |
0,047656 |
0,047656 |
0,047656 |
0,063542 |
||
4 |
0,5 |
0,6 |
|
|
0,075 |
0,075 |
0,075 |
0,075 |
0,05 |
5 |
0,625 |
0,88125 |
0,110156 |
0,110156 |
0,110156 |
0,110156 |
0,146875 |
||
6 |
0,75 |
1,225 |
|
|
0,153125 |
0,153125 |
0,153125 |
0,153125 |
0,102083 |
7 |
0,875 |
1,63125 |
0,203906 |
0,203906 |
0,203906 |
0,203906 |
0,271875 |
||
8 |
1 |
2,1 |
|
|
0,2625 |
0 |
0,2625 |
0,13125 |
0,0875 |
|
|
|
|
|
|
|
|
|
|
|
Ответ |
|
|
|
|
0,646875 |
0,896875 |
0,771875 |
0,766667 |
Программа вычисления интеграла методом парабол (Симпсона) представлена на рис. 5.6.
CLS
REM LR-5-3, m=13, n=5
DEF FNF(X)=2*X^2+0.1
DATA 0,1,4
READ A,B,N
H=(B-A)/N/2
S=0
X=A
1S=S+H*(FNF(X)+4*FNF(X+H)+FNF(X+2*H))/3
X=X+2*H
IF X<B-H THEN 1 PRINT ²S=²; S END
Рис. 5.6. Программа вычисления интеграла методом парабол (Симпсона).
9
6.Решение задачи Коши для обыкновенных дифференциальных уравнений.
Взависимости от числа независимых переменных дифференциальные уравнения делятся на две категории:
- обыкновенные дифференциальные уравнения, содержащие одну
независимую переменную; - уравнения с частными производными, содержащие несколько
независимых переменных.
Обыкновенными дифференциальными уравнениями называются такие уравнения, которые содержат одну или несколько производных от искомой функции y=y(x):
F(x,y,y′,...,y(n))=0 , |
(6.1) |
где х - независимая переменная, n - порядок дифференциального уравнения. Уравнения первого и второго порядков записываются в виде:
F(x,y,y′)=0, F(x,y,y′,y′′)=0.
Записи: y′=f(x,y), |
y′′=f(x,y,y′) |
|
(6.2) |
|
называются |
уравнениями, |
разрешенными |
относительно |
старшей |
производной.
Линейным дифференциальным уравнением называется уравнение, линейное относительно искомой функции и ее производных. Например,
y′- x2 y = sin(x) - линейное уравнение первого порядка.
Решением дифференциального уравнения (6.1) называется всякая функция y=ϕ(x), которая после ее подстановки в уравнение превращает ее в тождество.
Общее решение обыкновенного дифференциального уравнения n-го
порядка содержит n произвольных постоянных c1,c2,...,cn |
|
y=ϕ( c1,c2,...,cn) |
(6.3) |
Частное решение дифференциального уравнения получается из общего, если произвольным постоянным придать определенные значения.
Для уравнения первого порядка общее решение зависит от одной произвольной постоянной:
y=ϕ(x,c). |
(6.4) |
10
Если постоянная принимает определенное значение с=с0, то получим частное решение: y=ϕ(x,c0).
Дадим геометрическую интерпретацию дифференциального уравнения первого порядка (6.2).
Поскольку производная y′ характеризует наклон касательной κ интегральной кривой в данной точке, то при y′=κ=const из (6.2) получим f(x,y)=κ - уравнение линии постоянного наклона, называемой изоклиной. Меняя κ, получаем семейство изоклин.
Приведем геометрическую интерпретацию общего решения (6.4). Это решение описывает бесконечное множество интегральных кривых с параметром c, а частному решению соответствует одна кривая из этого семейства. Через каждую точку из области решения проходит одна интегральная кривая.
Для выделения некоторого частного решения уравнения первого порядка достаточно задать координаты (x0,y0) произвольной точки на данной интегральной кривой.
Для уравнений высших порядков для выделения частного решения из общего нужно задавать столько дополнительных условий, сколько произвольных постоянных в общем решении, т.е. каков порядок уравнения.
Если эти условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями х = x0, в которой они задаются, - начальной точкой.
Если же дополнительные условия задаются при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются граничными условиями.
Наиболее распространенным и универсальным численным методом решения дифференциальных уравнений является метод конечных разностей. Его сущность состоит в следующем. Область непрерывного изменения аргумента, заменяется дискретным множеством точек, называемых узлами, и задача считается решенной, если найдены неизвестные значения функции в этих точках. Численные методы решения дифференциальных уравнений методом конечных разностей проводятся в два этапа:
1.Аппроксимация дифференциального уравнения системой линейных и нелинейных разностных уравнений;
2.Решение полученной системы разностных уравнений.
Разностные методы позволяют находить только конкретное (частное) решение, однако необходимо подчеркнуть, что эти методы в настоящее время являются основными при решении дифференциальных уравнений с помощью ЭВМ.
Одним из простейших разностных методов решения обыкновенного дифференциального уравнения является одношаговый метод Эйлера.
Пусть требуется решить задачу Коши для уравнения первого порядка:
