
ЧМ-2
.pdf
|
|
11 |
y′=f(x ,y), |
y(x0)= y0 |
(6.5) |
на отрезке [а,b].
На данном отрезке выбираем некоторую совокупность узловых точек a=x0< x1<x2< ...<x n=b и разложим искомую функцию y(x) в ряд Тейлора в их окрестностях.
6.1. Метод Эйлера.
Если отбросить все члены, содержащие производные второго и более высоких порядков, и считать узлы равностоящими, т.е. xi=xi+1-xi=h, то это разложение можно записать в виде:
y(xi+1) = yi+1 = yi + h f(xi,yi), i =0,1,...,n-1. |
(6.6) |
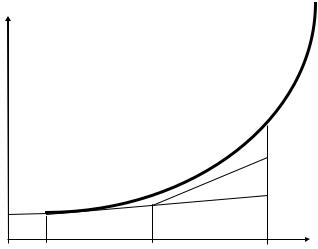
Соотношения (6.6) имеют вид рекурентных формул, с помощью которых значение сеточной функции yi+1 в любом узле xi+1 вычисляется по ее значению yi в предыдущем узле xi. На каждом шаге погрешность имеет порядок O(h2). На рис. 6.1 дана геометрическая интерпретация метода Эйлера. В силу невысокой точности формулой Эйлера редко пользуются в практических расчетах и используют более точные методы. Например, модифицированный метод Эйлера.
y
|
|
|
|
|
|
|
|
y2 |
|
|
y0 |
|
|
|
|
y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x0 |
x1 |
|
x2 |
x |
|
|
|||
|
Рис. 6.1. Метод Эйлера. |
|
|
|
|
|
||||
Пример: |
Решить |
задачу |
Коши |
методом |
Эйлера |
для |
||||
дифференциального уравнения |
|
|
|
|
|
|
||||
y′=x2+y, y(0)= 1 |
на отрезке [0;0,3] с шагом 0,1. |
|
|
|||||||

12
Решение: По формуле (6.6) вычислим значение y1
y1 = y0 + h f(x0,y0) = 1 +0,1 (02 +1) = 1,1
Аналогично вычисляются последующие значения функции в узловых точках
y2 = y1 + h f(x1,y1)=1,1+0,1·(0,12+1,1) = 1,211
y3 = y2 + h f(x2,y2)=1,211+0,1·(0,22+1,211) = 1,3361
Сеточную функцию записываем в виде таблицы
x |
|
0 |
|
0,1 |
|
0,2 |
|
0,3 |
|
|
|
|
|||||
y |
|
1 |
|
1,1 |
|
1,211 |
|
1,3361 |
|
|
|
|
Программа решения задачи Коши методом Эйлера дана на рис. 6.2.
CLS
REM LR-6-1, m=13, n=5
DEF FNY(X,Y)=X^2+Y
DATA 0, 0.3, 1, 0.1
READ A, B, Y0, H
PRINT A;Y0
X=A: Y=Y0
1Y=Y+ FNY(X,Y)*H X=X+H
PRINT X;Y
IF X<B THEN 1 END
Рис. 6.2. Программа решения задачи Коши методом Эйлера.
6.2. Модифицированный метод Эйлера.
Модифицированный метод Эйлера позволяет уменьшить погрешность на каждом шагу до величины O(h3) вместо O(h2) в обычном методе (6.6). Запишем разложение функции в ряд Тейлора в виде:
yi+1 = yi + h y′i + h2/2 y′′i + O(h3). |
(6.7) |
Аппроксимируем вторую производную с помощью отношения
конечных разностей: y′′i = (y′i+1 - y′i) / h.
Подставляя это соотношение в (6.7) и пренебрегая членами порядка O(h3), получаем:
yi+1 = yi + h/2 [f(xi,yi) + f(xi+1,yi+1)]. |
(6.8) |
13
Полученная схема является неявной, поскольку искомое значение yi+1 входит в обе части соотношения (6.8) и его нельзя выразить явно. Если имеется хорошее начальное приближение yi, то можно построить решение с использованием двух итераций следующим образом. Сначала по формуле (6.6) вычисляют первое приближение y i+1
y i+1= yi + h f(yi,xi). |
(6.9) |
Найденное значение подставляется вместо yi+1 в правую часть |
|
соотношения (6.8) и находится окончательное значение |
|
yi+1 = yi + h[f(xi,yi) + f(xi+1, y i+1)]/2, |
i=0,1,...,n-1. |
(6.10) |
|
На рис. 6.3 дана геометрическая интерпретация первого шага вычислений при решении задачи Коши модифицированным методом Эйлера.
y
y1
y 1
y0
0 |
x0 |
h/2 |
h/2 |
x1 x |
Рис. 6.3. Модифицированный метод Эйлера.
Пример: Решить задачу Коши модифицированным методом Эйлера для дифференциального уравнения
y′=x2+y, y(0)= 1 на отрезке [0;0,3] с шагом 0.1.
Решение: По формуле (6.9) вычислим первое приближение y 1
y 1 = y0 + h f(x0,y0) = 1 +0,1 (02 +1) = 1,1
Используя формулу (6.10), находим окончательное значение в точке x1=0.1
y1=y0+h [f(x0,y0)+f(x1, y 1)]/2=1+0,1· (02+1+0,12+1,1)/2=1,1055

14
Аналогично вычисляются последующие значения функции в узловых точках
y 2 = y1 + h f(x1,y1)=1,1055+0,1· (0,12+1,1055) = 1,21705
y2=y1+h[f(x1,y1)+f(x2,y 2)]/2=
=1,1055+0,1· (0,12+1,1055+0,22+1,21705)/2=1,224128
y 3 = y2 + h f(x2,y2)=1,224128+0,1· (0,22+1,224128) = 1,350541
y3=y2+h[f(x2,y2)+f(x3,y 3)]/2=
=1,224128+0,1· (0,12+1,224128+0,22+1,350541)/2=1,355361
Сеточную функцию записываем в виде таблицы
x |
|
0 |
|
0.1 |
|
0.2 |
|
0.3 |
|
|
|
|
|||||
y |
|
1 |
|
1.1055 |
|
1,224128 |
|
1,355361 |
|
|
|
|
Программа решения задачи Коши модифицированным методом Эйлера дана на рис. 6.4.
CLS
REM LR-6-2, m=13, n=5
DEF FNY(X,Y)=X^2+Y
DATA 0, 0.3, 1, 0.1
READ A, B, Y0, H
PRINT A;Y0
X=A: Y=Y0
1Y1=Y+ FNY(X,Y)*H Y=Y+H*(FNY(X,Y)+FNY(X+H,Y1))/2 X=X+H
PRINT X;Y
IF X<B THEN 1 END
Рис. 6.4. Программа решения задачи Коши модифицированным методом Эйлера.
Существуют и другие одношаговые методы. Наиболее распространенным из них является метод Рунге-Кутта.
6.3. Метод Рунге-Кутта.
15
На основе метода Рунге-Кутта могут быть построены разностные схемы разного порядка точности. Наиболее употребительной является следующая схема четвертого порядка:
yi+1 = yi + (k0 + 2k1 + 2k2 + k3) /6. |
(6.11) |
|
где |
|
|
k0 |
= h f(xi, yi), |
|
k1 |
= h f(xi+h/2, yi+ k0 /2), |
|
k2 |
= h f(xi+h/2, yi+ k1 /2), |
(6.12) |
k3= h f(xi+h, yi+ k2).
Таким образом, метод Рунге-Кутта требует на каждом шаге четырехкратного вычисления правой части уравнения. Однако это окупается повышенной точностью, что дает возможность проводить счет с относительно большим шагом.
Пример: Решить задачу Коши методом Рунге-Кутта для дифференциального уравнения
y′=x2+y, y(0)= 1 на отрезке [0,0.3] с шагом 0.1.
Решение: По формулам (6.12) вычислим значения k0 , k1, k2, k3
k0=h f(x0,y0)=0,1·(02+1)=0,1
k1=h f(x0+h/2, y0+k0 /2)=0,1· ((0+0,1/2)2+1+0,1/2)=0,10525
k2=h f(x0+h/2,y0+k1 /2)=0,1· ((0+0,1/2)2+1+0,10525/2)=0,105513
k3= h f(x0+h, y0+ k2)=0,1· ((0+0,1)2+1+0,105513)= 0,111551
Используя формулу (6.11), находим значение y1 в точке x1=0.1
y1=y0+(k0+2k1+2k2+k3)/6=
=1+(0,1+2·0,10525+2·0,105513+0,111551)/6=1,105513
Аналогично вычисляются последующие значения функции в узловых точках
k0=h f(x1,y1)=0,1· (0,12+1,105513)=0,111551
k1=h f(x1+h/2,y1+k0/2)=0,1· ((0,1+0,1/2)2+1,105513+0,111551/2)=0,118379
k2=h f(x1+h/2,y1+k1/2)=0,1· ((0,1+0,1/2)2+1,105513+0,118379/2)=0,11872
k3= h f(x1+h,y1k2)=0,1· ((0,1+0,1)2+1,105513+0,11872)=0,126423
y2=y1+(k0+2k1+2k2+k3)/6=
16
=1,105513+(0,111551+2·0,118379+2·0,11872+0,126423)/6=1,224208
k0=h f(x2,y2)=0,1· (0,22+1,224208)=0,126421
k1=h f(x2+h/2, y2+k0 /2)=0,1· ((0,2+0,1/2)2+1,224208+0,126421/2)=0,134992
k2=h f(x2+h/2,y2+k1 /2)=0,1· ((0,2+0,1/2)2+1,224208+0,134992/2)=0,13542
k3=h f(x2+h,y2+k2)=0,1· ((0,2+0,1)2+1,224208+0,13542)=0,144963
y3=y2+(k0+2k1+2k2+k3)/6=
=1,224208+(0,126421+2·0,134992+2·0,13542+0,144963)/6=1,359576
Сеточную функцию записываем в виде таблицы
x |
|
0 |
|
0.1 |
|
0.2 |
|
0.3 |
|
|
|
|
|
|
|||||
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
y |
|
1 |
|
1,105513 |
|
1,224208 |
|
1,359576 |
|
|
|
|
|
||||||
Программа решения задачи Коши методом Рунге-Кутта дана на рис.
6.5.
CLS
REM LR-6-3, m=13, n=5
DEF FNY(X,Y)=X^2+Y
DATA 0, 0.3, 1, 0.1
READ A, B, Y0, H
PRINT A;Y0
X=A: Y=Y0
1K0 = H*FNY(X,Y)
K1 = H*FNY(X+H/2,Y+K0/2)
K2 = H*FNY(X+H/2,Y+K1/2)
K3 = H*FNY(X+H,Y+K2) Y=Y+(K0+2*K1+2*K2+K3)/6 X=X+H
PRINT X;Y
IF X<B THEN 1 END
Рис. 6.5. Программа решения задачи Коши методом Рунге-Кутта.
6.4.Разностные методы решения краевой задачи для обыкновенного дифференциального уравнения.
Линейная краевая задача имеет |
вид: |
y′′+ p(x) y′+ q(x) y = f(x) |
(6.12) |

|
|
|
17 |
|
|
|
a1y(a) + a2 y¢(a) = a3 |
, |
|
|
(6.13) |
||
|
|
|
|
|
|
|
b1 y(b)+ b2 y¢(b) = b3 |
, |
|
|
|
||
при |a1|+|a2| ¹ 0 |
|b1|+|b2| ¹ 0 xÎ[a,b]. |
|
|
|||
Решение |
задачи |
(6.12)-(6.13) |
проводится |
в |
следующей |
|
последовательности:
1. Определение сетки:
Отрезок [a,b] делится на конечное число частей:
y1 |
y2 |
. . . yk |
. . . . . yn-1 |
yn |
yn+1 |
|
|
||
| |
| |
| |
| |
| |
| |
|
|
|
|
x1=a |
x2 |
. . . xk |
. . . . . xn-1 |
xn |
xn+1=b |
x |
|||
|
|
|
____ |
|
|
|
|
|
|
xk=x1 + (k - 1)h; |
k=1,n+1; h=(b-a)/n. |
|
|
|
|
||||
x1, xn+1 - краевые точки, x2, x3, . . |
. , xn-1, xn - внутренние точки. |
||||||||
2. Определение сеточной функции yi = y(xi): |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
x1 |
|
x2 |
|
x3 |
... |
|
|
xn+1 |
|
у1 |
|
у2 |
|
у3 |
... |
|
|
уn+1 |
|
3. Аппроксимация уравнения:
Aппроксимация производных y¢(x) и y¢¢(x) центральными
конечноразностными аналогами имеет вид: |
|
y¢(xk)=(y(xk+h)-y(xk-h))/2h+O(h2), |
(6.14) |
y¢¢(xk)=(y(xk+h)-2y(xk)+y(xk-h))/h2+O(h2). |
(6.15) |
Подстановка полученных соотношений (6.14)¾(6.15) в уравнение
(6.12) дает
(yk+1-2yk+yk-1)/h2+pk(yk+1-yk-1)/2h+qkyk=fk, |
(6.16) |
где yk=y(xk), pk=p(xk), qk=q(xk), fk=f(xk). |
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
yk+1-2yk+yk-1+ |
pk h |
yk+1- |
|
pk h |
yk-1+qkh2yk=fkh2, |
|
||||||||
|
2 |
|
|
|||||||||||
2 |
|
|
|
|
|
|
|
|
|
|||||
(1- |
pk h |
) yk-1+(qkh2-2)yk+(1+ |
pk h |
) yk+1=fkh2. |
|
|||||||||
|
2 |
|
||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
После этих преобразований уравнение (6.16) можно представить в |
||||||||||||||
виде: |
___ |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||
akyk-1+ckyk+bkyk+1=dk, |
k=2,n |
(6.17) |
||||||||||||
|
|
где ak= 1- |
pk h |
, |
bk= 1+ |
pk h |
, ck=gkh2-2, |
dk= fkh2. |
||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|||
Для краевых условий применяем следующие разностные формулы:
y′(xk)=(y(xk+1)−y(xk))/h,
или
y′(а)=(y′(x1)=(y(x2)−y(x1))/h=(y2−y1)/h , y′(b)=y′(x n+1)=(y(x n+1)−y(x n))/h=(y n+1−y n)/h .
Подставляя в краевые условия (8.2)-(8.3) получим:
α1y1 + α2 (y2−y1)/h = α3 , |
|
||
β1 y(b)+ β2 (y n+1−y n)/h |
= β3 . |
|
|
После преобразований краевые условия (6.13) запишем в виде: |
|||
c1y1 + b1y2 = d1 , |
|
(6.18) |
|
an+1yn + c n+1yn+1 = d n+1 , |
|
(6.19) |
|
где |
c1 = α1 h − α2; |
b1 = α2; |
d1 = α3 h; |
|
an+1 = - β2; cn+1 = β1 h + β2; |
d n+1 = β3 h. |
|
Таким образом, для определения (n+1) неизвестных величин yk |
|||
составляется (n+1) уравнений вида: |
|
||
c1y1 + b1y2 = d1 , |
k=1 |
|
|
|
|
___ |
|
akyk-1+ckyk+bkyk+1=dk, |
k=2,n |
(6.20) |
|
an+1yn + c n+1yn+1 = d n+1 , |
k=n+1. |
|
|

19
Система (n+1) уравнений (8.10) решается методом прогонки.
Пример: Решить краевую задачу методом конечных разностей с шагом h = 0,1:
y′′ - xy′+ 2xy = 0,8 y(1,2) - 0,5y′(1,2) = 1 y′(1,5) = 2.
Решение. Решение проводим в следующей последовательности: 1. Определение сетки:
| |
| |
| |
| |
|
x1=1,2 |
x2=1,3 |
x3=1,4 |
x4=1,5 |
x |
x1, x4 - краевые точки, x2, x3 - внутренние точки.
|
|
2. Определение сеточной функции yi = y(xi): |
|
||||
|
|
|
|
|
|
|
|
|
x1 |
|
x2 |
x3 |
x4 |
|
|
|
у1 |
|
у2 |
у3 |
у4 |
|
|
|
|
3. Аппроксимация уравнения: |
|
||||
при x1=1,2: |
|
у1-0,5(y2−y1)/0,1 = 1 |
(6.21) |
||||
при x2=1,3: |
|
(у3-2у2+у1)/0,01-1,3(y3−y1)/0,2+2*1,3y2=0,8 |
(6.22) |
||||
при x3=1,4: |
|
(у4-2у3+у2)/0,01-1,4(y4−y2)/0,2+2*1,4y3=0,8 |
(6.23) |
||||
при x4=1,5: |
|
(y4−y3)/0,1 = 2. |
(6.24) |
||||
Полученная система четырех линейных уравнений с четырьмя неизвестными у1, у2, у3 и у4 решается методом прогонки.
у1-5(y2−y1) = 1
100(у3-2у2+у1) -6,5(y3−y1)+2*1,3y2=0,8 100(у4-2у3+у2) -7(y4−y2)+2*1,4y3=0,8 10(y4−y3) = 2
6у1 |
- 5y2 |
= 1 |
106,5у1 |
- 197,4у2 + 93,5у3 |
= 0,8 |
|
107у2 -197,2у3+93у4 = 0,8 |
|
20
−10y3+10y4 = 2
Значения ai; bi; ci; di; i=1, 2, 3, 4 записываем в виде таблицы 6.1.
Таблица 6.1
i |
ai |
bi |
ci |
di |
|
|
|
|
|
1 |
0 |
6 |
- 5 |
1 |
2 |
106,5 |
- 197,4 |
93,5 |
0,8 |
3 |
107 |
-197,2 |
93 |
0,8 |
4 |
-10 |
10 |
0 |
2 |
Прямой ход прогонки. Определяем прогоночные коэффициенты Ui и
Vi (i=1,2,3,4)
U1=-c1/b1=5/6=0,833333
V1=d1/b1=1/6=0,166667
U2=-c2 /(b2 + a2U1)=- 93,5/(-197,4+106,5*0,833333)= 0,860561 V2=(d2-a2V1)/(b2+a2U1)= =(0,8-106,5·0,166667)/(-197,4+106,5·0,833333)=0,156006 U3=-c3 /(b3+a3U2)=-93/(-197,2+107·0,860561)=0,884703
V3=(d3-a3V2)/(b3+a3U2)=(0,8-107·0,156006)/(-197,2+107·0,860561)=0,151186
U4=-c4 /(b4+a4U3)=0
V4=(d4-a4V3)/(b4+a4U3)=(2+10·0,151186)/(10-10·0,884703)=3,045925
Обратный ход прогонки. По формулам (2.7) вычисляем все xi;
i=4,3,2,1).
Поскольку cn = 0, то y4 = V4 = 3,045925.
Далее вычисляем y3, y2, y1
y3 = U3 y4 + V3 = 0,884703·3,045925+0,151186=2,845925
y2 = U2 y3 + V2 =0,860561·2,845925+0,156006=2,605098
y1 = U1 y2 + V1 =0,833333·2,605098+0,166667=2,337581
Сеточную функцию yi = y(xi) записываем в виде таблицы
