39.Метод прогонки.

При решении практических задач получаются системы, матрицы которых содержат много нулей, то говорят, что система имеет слабо заполненную матрицу. Эти нули обычно располагаются массивами в определённых местах матрицы.

Если применить к таким системам метод Гаусса, то нулевые элементы будут вовлечены в вычислительный процесс, что не желательно. Поэтому, созданы специальные методы, позволяющие обходить нулевые элементы. Одним из таких методов является метод прогонки, он применяется к системам с ленточной матрицей.

Пусть дана система:

(2 )

b₁x₁+c₁x₁ =d₁

a1x1+b2x2+C2x3=d2

a3x2+b3x3+C3x4=d3

anxn-1+bnxn=d_n

система (2) имеет ленточную матрицу, так называемую трех диагональную матрицу. Метод прогонки является частным случаем, метода Гаусса и состоит из прямого и обратного хода. Прямой ход состоит в исключении элементов системы матрицы (2), лежащих ниже главной диагонали:

Aij=2;n. i=2;n Для этого из 1-го уравнения выражают х₁: x1=-(c1/bx)x2+d1/b1

u₁= -c₁/b₁ , v₁=d₁/b_{1 (3)} (3)

X1=U1X2+V1

и подставляют его во 2-ое уравнение вместо х₁:

a2(U1X2+V1) +b2X2+C2X3=d2

(a2U1+b2)X2+C2X3=d2-a2V1

в результате, из 2-го исключается х₁. Из полученного выражаем х₂:

X2= - (C2/(d2U1+b2))X3+(d2-a2V1)/(a2U1+b2)

U2= -(C2/ (d2U1+b2)

V1= (d2-a2V1)/ (a2U1+b2) (4)

X₂= U₂x₃+ v₁,

полученное выражение х₂ в 3 -е уравнение, чтобы исключить х₂ и т.д., то на i-ом шаге исключения получим формулу:

ui ,vi- называют прогоночными коэффициентами, т.к. в результате выполнения прогонки система (2) преобразуется в к виду:

х, = UiXi-1+Vi , i=1,n (6)

Используя формулы (6) можно выполнить обратный ход прогонки , если i=n X_n=u_nX_n-1+V_n , но u_n=0,. т.к. с_п=0, следовательно: X_n=V_n

Обратный ход программы:

xn=Vn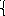

xn-1 = Un-1 xn+Vn-1 xn-2 = Un-2 xn+Vn-1 (7)

…

x1=U1x2+V1

Систему (2) можно записать в следующем виде

aixi-1+bixi+cxi+1=di

i=1,n ai=0, Cn=0

39.Метод прогонки.

При решении практических задач получаются системы, матрицы которых содержат много нулей, то говорят, что система имеет слабо заполненную матрицу. Эти нули обычно располагаются массивами в определённых местах матрицы.

Если применить к таким системам метод Гаусса, то нулевые элементы будут вовлечены в вычислительный процесс, что не желательно. Поэтому, созданы специальные методы, позволяющие обходить нулевые элементы. Одним из таких методов является метод прогонки, он применяется к системам с ленточной матрицей.

Пусть дана система:

(2 )

b₁x₁+c₁x₁ =d₁

a1x1+b2x2+C2x3=d2

a3x2+b3x3+C3x4=d3

anxn-1+bnxn=d_n

система (2) имеет ленточную матрицу, так называемую трех диагональную матрицу. Метод прогонки является частным случаем, метода Гаусса и состоит из прямого и обратного хода. Прямой ход состоит в исключении элементов системы матрицы (2), лежащих ниже главной диагонали:

Aij=2;n. i=2;n Для этого из 1-го уравнения выражают х₁: x1=-(c1/bx)x2+d1/b1

u₁= -c₁/b₁ , v₁=d₁/b_{1 (3)} (3)

X1=U1X2+V1

и подставляют его во 2-ое уравнение вместо х₁:

a2(U1X2+V1) +b2X2+C2X3=d2

(a2U1+b2)X2+C2X3=d2-a2V1

в результате, из 2-го исключается х₁. Из полученного выражаем х₂:

X2= - (C2/(d2U1+b2))X3+(d2-a2V1)/(a2U1+b2)

U2= -(C2/ (d2U1+b2)

V1= (d2-a2V1)/ (a2U1+b2) (4)

X₂= U₂x₃+ v₁,

полученное выражение х₂ в 3 -е уравнение, чтобы исключить х₂ и т.д., то на i-ом шаге исключения получим формулу:

ui ,vi- называют прогоночными коэффициентами, т.к. в результате выполнения прогонки система (2) преобразуется в к виду:

х, = UiXi-1+Vi , i=1,n (6)

Используя формулы (6) можно выполнить обратный ход прогонки , если i=n X_n=u_nX_n-1+V_n , но u_n=0,. т.к. с_п=0, следовательно: X_n=V_n

Обратный ход программы:

xn=Vn

xn-1 = Un-1 xn+Vn-1 xn-2 = Un-2 xn+Vn-1 (7)

…

x1=U1x2+V1

Систему (2) можно записать в следующем виде

aixi-1+bixi+cxi+1=di

i=1,n ai=0, Cn=0

Алгоритм метода прогонки:

1)Ввести aj;bi,Ci,di . i=1,n

2)Вычислить u_i,v_i по формулам (5)

3)Вычислить xi по формулам (7)

4)Вычислить невязки: r_i=d_i- a_ix_i-₁-b_ix_i-c_ix_i-₁

5)Напечатать x_i, r_i (i=1,n).

Программа: INPUT n

DIM a(n),b(n),c(n),d(n),x(n+1),u(n),v(n)

FOR i=1 TO n

INPUT a(i),b(i),c(i),d(i)

NEXT

FOR i=1 TO n

Ui=- c(i)\( d(i)*u(i-1)+b(i))

Vi=( d(i)-a(i)- v(i-1))\ (d(i)*u(i-1)+b(i))

FOR i=1 TO n STEP -1

x(i)=u(i)*x(i-1) +V(i)

NEXT

FOR i=1 TO n

PRINT x(i), d(i)-a(i)*x(i-1)-b(i)*x(i)-c(i)*x(i+1)

END.

Например: Решить методом прогонки систему: г

5х1+х2=4

2х₁-4х₂+х₃=7

х2=3х3=2

Исходные данные :

a₁=0 ,b₁=5, c₁=1 , d₁₌₄

a2=2, b2=-4, C2=1, d2=7,

a3=1, b3=3, C3=0, d3=2,

u₁=-c₁/b₁=-1/5

V1=d1/b1=4/5

U2=-C2/(a1+b2)=5/22

V2=(d2-a2U1)/(a2U1+b2)=-27/22

U3=0

V3= (d3-a3V2)/(a3U2+b3)=1

и обратный ход:

x3=V3=1

x₂=U₂x₃+v₂=5/22*1-27/22=-1

x1=U1x2+V1=-1/5 * (-1 )+4/5=1

Достаточное условие устойчивости прогонки (но не необходимое).

Если выполняется условие диагонального преобладания для основной матрицы системы (2):

|b₁|>=|a_i|+ |ci| , i=1,n ,.. то в формуле (5) не возникает деления на ноль, не происходит накопление погрешностей.