
контрольная работа №4
.docx
Задание 4.1.
Вычислить неопределенные интегралы.
Непосредственное интегрирование.
а).
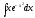 ;
;
б).
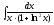 ;
;
в).
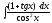 .
.
Интегрирование по частям.
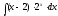 .
.
Интегрирование дробно-рациональных функций.
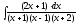 .
.
Интегрирование иррациональных функций. Вычисление определенного интеграла.
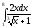 .
.
Решение.
а). Используем метод замены переменной для вычисления указанного неопределенного интеграла.
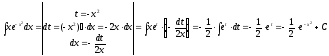 .
.
б). Используем метод замены переменной для вычисления указанного неопределенного интеграла.
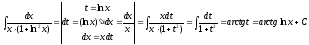 .
.
в). Используем метод замены переменной для вычисления указанного неопределенного интеграла.
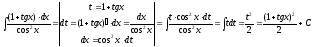 .
.
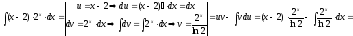
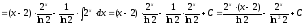 .
.
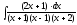 .
.
Разложим подынтегральное выражение на сумму простейших дробей, используя метод неопределенных коэффициентов.
Разложение дроби на простейшие имеет вид:
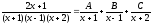 .
.
Освобождаясь от знаменателей, получаем:
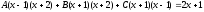 ;
;
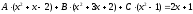 ;
;
 .
.
Приравниваем
коэффициенты одинаковых степеней
 :
:
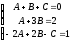 .
.
Решаем полученную систему уравнений с тремя неизвестными:
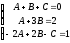 ;
;
 ;
;
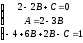 ;
;
 ;
;
 ;
;
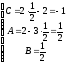 .
.
Следовательно,
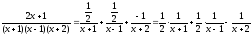 .
.
Тогда, получим:
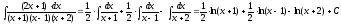 .
.
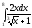 .
.
Сначала решим соответствующий неопределенный интеграл:

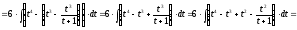
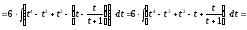
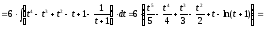
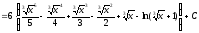 .
.
Используя формулу Ньютона-Лейбница, вычисляем указанный определенный интеграл:
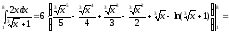
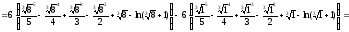
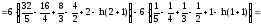
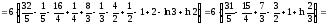
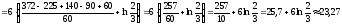 .
.
Задание 4.2.
Найти длину
указанной кривой:
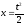 ,
,
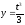 ,
,
 .
.
Решение.
Для определения
длины указанной линии, которая задана
параметрически, используем соответствующую
формулу:
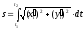 .
.
В нашем случае получим:
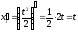 ;
;
 ;
;
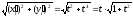 ;
;
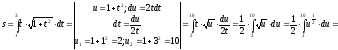
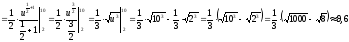 .
.
Задание 4.3.
Изменить порядок интегрирования, сделать чертеж.
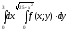 .
.
Решение.
Так как внутренний
интеграл берется по
 ,
то пределы внутреннего интеграла
показывают, какими линиями область
интегрирования ограничена снизу и
сверху. Уравнения этих линий должны
быть соответственно
,
то пределы внутреннего интеграла
показывают, какими линиями область
интегрирования ограничена снизу и
сверху. Уравнения этих линий должны
быть соответственно
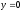 и
и
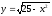 (полукруг в первой и второй координатных
четвертях с центром в начале координат
и радиусом равным 5). Пределы внешнего
интеграла указывают промежуток изменения
переменной
(полукруг в первой и второй координатных
четвертях с центром в начале координат
и радиусом равным 5). Пределы внешнего
интеграла указывают промежуток изменения
переменной
 в области интегрирования от 0 до 3.
Построим область интегрирования.
в области интегрирования от 0 до 3.
Построим область интегрирования.
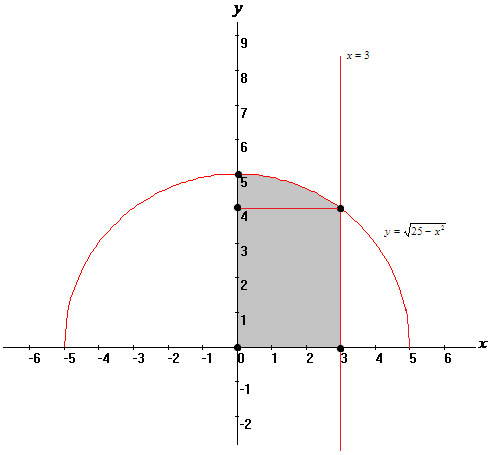
Решая уравнения
заданного полукруга относительно
 ,
получим:
,
получим:

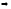
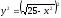 ;
;
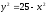 ;
;
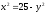 ;
;
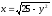 .
.
Теперь приступаем
к изменению порядка интегрирования в
заданном интеграле, то есть будем
внутреннее интегрирование производить
по
 ,
а внешнее – по
,
а внешнее – по
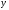 .
Учитывая чертеж, получим две области:
.
Учитывая чертеж, получим две области:
1). первая ограничена
по переменной
 от 0 до 3, а по переменной
от 0 до 3, а по переменной
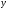 от 0 до 4;
от 0 до 4;
2). вторая ограничена
справа полукругом
 ,
а слева –
,
а слева –
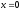 ;
по переменной
;
по переменной
 имеем ограничения от 4 до 5.
имеем ограничения от 4 до 5.
Объединяя полученные две области, получим:

Задание 4.4.
Вычислить
криволинейный интеграл
 вдоль линии
вдоль линии
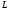 – контур треугольника
– контур треугольника
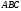 (в положительном направлении), причем
(в положительном направлении), причем
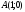 ,
,
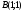 ,
,
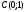 .
.
Решение.
Сделаем схематический чертеж указанного контура:
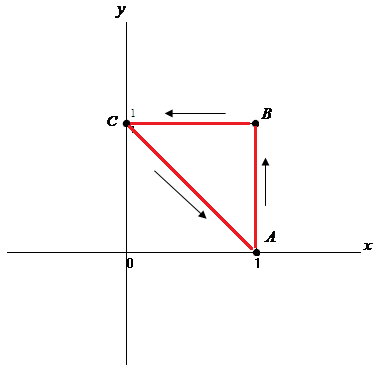
Запишем уравнения полученных прямых:
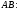
 ;
;
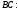
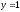 ;
;
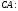
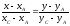 ;
;
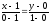 ;
;
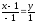 ;
;
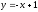 .
.
1). Вычислим указанный
криволинейный интеграл вдоль линии
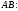
 .
.
Определяем необходимые данные для расчета криволинейного интеграла:
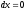 .
.
Тогда, получим:
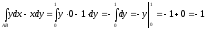 .
.
2). Вычислим указанный
криволинейный интеграл вдоль линии
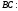
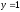 .
.
Определяем необходимые данные для расчета криволинейного интеграла:
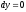 .
.
Тогда, получим:
 .
.
3). Вычислим указанный
криволинейный интеграл вдоль линии

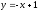 .
.
Определяем необходимые данные для расчета криволинейного интеграла:
 .
.
Тогда, получим:
 .
.
Следовательно,
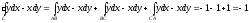 .
.
