- •1) Понятие об информации
- •2) Предмет и задачи информатики.
- •3) Представление числовой текстовой информации в эвм.
- •4) Представление графической и звуковой информации в эвм
- •5) Структура эвм по фон Нейману. Принципы фон Неймана.
- •6) Классификация эвм. Персональные компьютеры.
- •1. Сверхбольшие (суперЭвм)
- •8) Внутреннее устройство пк:
- •9) Внешние устройства пк. Адаптеры и контроллеры.
- •10) Программное обеспечение пк. Классификация.
- •11) Операционные системы для пк.
- •1. «Переводчик» с программного языка на «железный», язык машинных кодов.
- •12) Операционная система Windows. Технологические принципы. (7)
- •13) Операционная система Windows. Функции, интерфейс, приёмы работы.
- •15) Основные операции, выполняемые над файловой структурой. Диспетчеры файлов (nc, проводник)
- •1. Наглядное отображение файловой системы на экране и удобные средства навигации;
- •2. Простой гибкий механизм диалога с ос;
- •3. Возможность манипуляции с файлами и информационный сервис.
- •16) Прикладное программное обеспечение. Обзор.
- •17) Текстовые редакторы. Основные понятия и способы работы.
- •18) Табличные расчеты и табличные процессоры
- •20) Компьютерные сети (общее понятие).
- •21) Локальные компьютерные сети (лвс).
- •22) Глобальные компьютерные сети.
- •23) Этапы решения задачи на эвм.
- •25) Языки программирования. Системы программирования.
- •26) Понятие моделирования. Математическое моделирование.
- •27) Метод деления отрезка пополам
- •29) Метод простой итерации
- •31) Итерационные методы решения слау
- •32) Аппроксимация функций. Постановка задач и методы ее решения.
- •36) Формулы численного интегрирования Формулы прямоугольников и трапеций.
- •37) Формулы численного интегрирования. Формула Симпсона. Правило Рунге.
- •38) Численное дифференцирование
- •39) Математические системы. Mathcad.
- •40) Задачи Коши для обыкновенных дифференциальных уравнений.
- •6.1.3. Метод Рунге-Кутта.
- •41) Краевая задача для обыкновенного дифференциального уравнения 2- го порядка.
29) Метод простой итерации
1)
Нелинейное уравнение
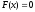 необходимо привести к виду
необходимо привести к виду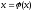 .
.
2)
Принять функцию
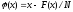 ,
гдеN ‑ неизвестная
постоянная величина, которая определяется
из условия сходимости метода простой
итерации
,
гдеN ‑ неизвестная
постоянная величина, которая определяется
из условия сходимости метода простой
итерации
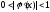 .
.
3) Определить N:
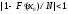 или
или
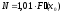 .
.
4)
Начальное приближение корня
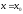 ,
подставляя в правую часть уравнения
,
подставляя в правую часть уравнения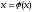 ,
получаем новое приближение.
,
получаем новое приближение.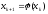
5) Далее подставляя каждый раз новое значение корня получаем последовательность значений.
6)
Итерационный процесс прекращается,
если результаты двух последовательных
итераций близки, т.е.
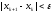 .
.
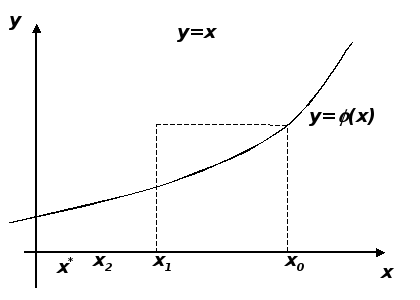
Геометрическая
интерпретация метода простой итерации.
Построим графики функций
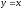 и
и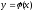 .
Корнем
.
Корнем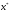 уравнения
уравнения является абсцисса пересечения кривой
является абсцисса пересечения кривой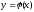 с прямой
с прямой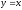 Взяв в качестве начальной точки
Взяв в качестве начальной точки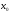 ,
строим ломаную линию. Абсциссы вершин
этой ломаной представляют собой
последовательные приближения корня
,
строим ломаную линию. Абсциссы вершин
этой ломаной представляют собой
последовательные приближения корня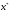 .
.
Function F(X)
F = X ^ 3...
End Function
Sub MPI()
a = Cells(1, 2)
n = Cells(2, 2)
e = Cells(3, 2)
Do
X = X - F(X) / n
Loop Until Abs(F(X) / n) < e
Cells(4, 2) = X
Cells(5, 2) = F(X)
End Sub
Методы решения СЛАУ. Метод прогонки.
Система
линейных алгебраических уравнений: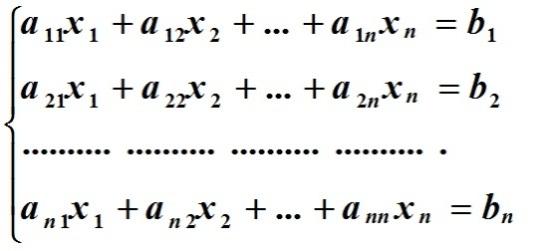
Методы решения систем уравнений:
- Прямые методы (точные): в предположении отсутствия ошибок округления получаем точное решение задачи за конечное число арифметических действий.
- Итерационные методы (приближенные): повторяющийся процесс приводит к решению в результате последовательных приближений.
Метод прогонки.
Применяется для решения систем уравнений с трехдиагональной (ленточной) матрицей, записываемой в виде:
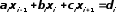
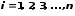 ,
,
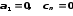 .
.
Состоит из прямого и обратного хода.
Прямой ход: исключение элементов матрицы системы, лежащих ниже главной диагонали. В каждом уравнении останется не более двух неизвестных и формулу
Обратный ход можно записать в следующем виде:
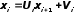 ,
,
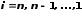
где
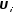 и
и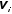 коэффициенты прямого хода прогонки
коэффициенты прямого хода прогонки
Поскольку
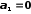 ,
то
,
то
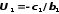 ,
, 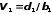
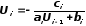
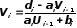
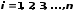
Поскольку
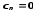 ,
то
,
то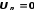 и
и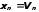 .
Далее вычисляем
.
Далее вычисляем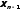 ,
,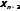 ,
...,
,
...,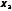 ,
,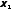 .
.
Вычисляем
невязки
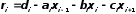 (
(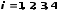 )
)
Sub program4()
Const n = 4
Dim a(n),b(n),c(n),d(n),u(n),v(n),x(n+1),r(n)
For i = 1 To n
a(i) = Cells(i + 1, 1)
b(i) = Cells(i + 1, 2)
c(i) = Cells(i + 1, 3)
d(i) = Cells(i + 1, 4)
u(i) = -c(i)/(a(i)*u(i-1)+b(i))
v(i) = (d(i)-a(i)*v(i-1))/(a(i)*u(i-1)+b(i))
Next i
For i = n To 1 Step -1
x(i) = u(i)*x(i+1)+v(i)
Next i
For i = 1 To n
r(i) = d(i)-a(i)*x(i-1)-b(i)*x(i)-c(i)*x(i+1)
Cells(i + 1, 6) = x(i)
Cells(i + 1, 7) = r(i)
Next i
End Sub
31) Итерационные методы решения слау
Метод Якоби
Суть
вычислений итерационными методами
состоит в следующем: расчет начинается
с некоторого заранее выбранного
приближения
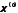 (начального приближения). Вычислительный
процесс, использующий матрицу
(начального приближения). Вычислительный
процесс, использующий матрицу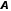 ,
вектор
,
вектор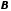 системы и
системы и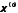 ,
приводит к новому вектору
,
приводит к новому вектору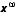 :
:
 ,
, 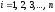
При
выполнении некоторых заранее оговоренных
условий процесс сходится при
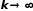 .
Сходимость метода простой итерации
обеспечивается при выполнении условия
преобладания диагональных элементов
матрицыA:
.
Сходимость метода простой итерации
обеспечивается при выполнении условия
преобладания диагональных элементов
матрицыA:
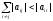 ,
, 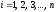 (2.13)
(2.13)
Заданная точность достигается при выполнении условия:
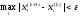
Метод Зейделя
В
методе Зейделя при нахождении
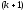 -ой
компоненты используются уже найденные
компоненты этой же итерации с меньшими
номерами, т.е. последовательность
итераций задается формулой:
-ой
компоненты используются уже найденные
компоненты этой же итерации с меньшими
номерами, т.е. последовательность
итераций задается формулой:
 ,
,