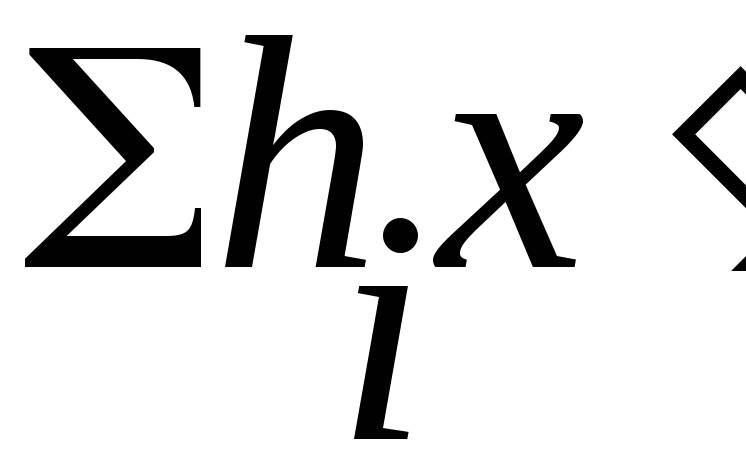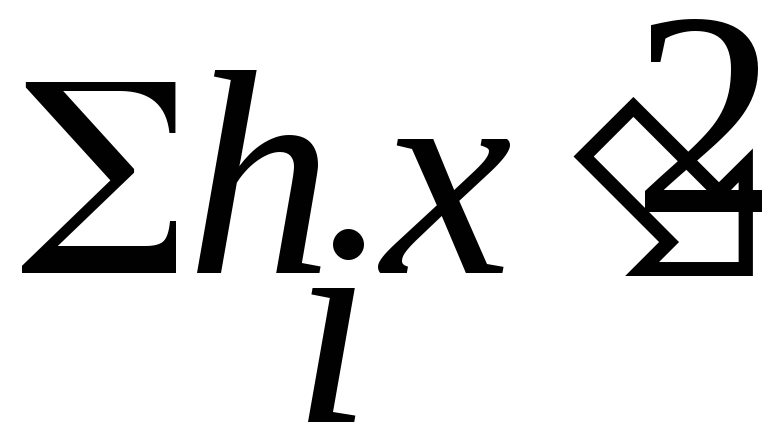- •1 . Корреляционный анализ
- •1.1. Построение рядов распределения по факторному и результативному признакам
- •1.2. Построение поля корреляции
- •1.3. Построение корреляционной таблицы
- •1.6. Измерение тесноты связи
- •2. Определение показателей вариации
- •2.1. Вычисление показателей вариации
- •3) Определение показателей вариации
- •2.2. Вычисление дисперсий
- •3. Анализ динамических рядов
- •3.1. Вычисление показателей динамики
- •3.2. Установление наличия тренда
- •3.3. Прогнозирование динамического ряда
- •3.4. Анализ полученных результатов
1.2. Построение поля корреляции
Поле корреляции строится как график зависимости между двумя параметрами. Оно строится в таком порядке: по горизонтальной линии откладываются измерения величин измерения величин одной переменной, а по вертикальной оси - другой переменной.

Рис. 1. Поле корреляции
1.3. Построение корреляционной таблицы
Для построения корреляционной таблицы на поле корреляции накладывается координатная сетка, соответствующая интервальным рядам распределения по факториальному и функциональному признакам.
Затем подсчитывается число точек (частот) в каждой клетке координатной сетки.
Результаты подсчетов по горизонтали и вертикали записываются в таблицу 1.8.
Таблица 1.8
Корреляционная таблица для зависимости y от x
|
Себестоимость строительно-монтажных работ, тыс.руб. |
Потери рабочего времени, чел-часов |
||||
|
243 – 256 |
256 – 269 |
269 – 282 |
282 – 295 |
Итого |
|
|
116 – 133,25 |
1 |
2 |
|
1 |
4 |
|
133,25 – 150,5 |
2 |
|
1 |
1 |
4 |
|
150,5 – 167,75 |
|
1 |
1 |
|
2 |
|
167,75 – 185 |
|
|
|
1 |
1 |
|
Итого |
3 |
3 |
2 |
3 |
|
Результаты расчетов, выполненные в таблице 1.8 позволяют сделать вывод о том, что наблюдается прямая линейная зависимость между значениями факторного признака х и функционального признака у. Следовательно связь между себестоимостью строительно-монтажных работ и потерями рабочего времени возможно описывается линейным уравнением.
1.4. Расчет эмпирической линии регрессии
После установления наличия корреляционной зависимости между функциональным и факторным признаками, приступают к следующему этапу статистического моделирования - к исследованию формы связи.
Под формой корреляционной связи понимают тип аналитической формулы, выражающей зависимость между изучаемыми величинами.
Необходимо установить, как изменяются средние значения y в связи с изменением x .
Рассчитываются
средние величины для каждого ряда
распределения по формуле средней
взвешенной арифметической величины:![]()
![]() (4),
(4),
где:
![]() -
средневзвешенное значение функции;
-
средневзвешенное значение функции;
y - центральные значения интервалов по функции;
m - абсолютные частоты вариантов y.
Для сокращения вычислений при определении средней арифметической используем метод отсчета от условного нуля.
Расчетная формула имеет вид
![]() (5),
(5),
при этом
![]() (6)
(6)
где:
![]() -
упрoщенные варианты y;
-
упрoщенные варианты y;
y - фактические варианты y;
сy- новое начало отсчета по оси y (условный нуль);
iy - интервал группировки по y.
Новое начало отсчета выбирается таким, образом, чтобы число наблюдений распределялось примерно поровну между положительным и отрицательным направлениями оси ординат.
В нашем примере примем условный нуль в третьем интервале по оси y, тогда сy=159,125 тыс.руб., а iy =17,25 тыс.руб.
Результаты расчетов представлены в таблице 1.9.
Упрощенные
варианты
![]() умножаются на частоты соответствующих
клеток корреляционной таблицы и
записываются в верхних правых углах
каждой клетки.
умножаются на частоты соответствующих
клеток корреляционной таблицы и
записываются в верхних правых углах
каждой клетки.
Первая итоговая строка и итоговый столбец таблицы 10 выражают абсолютные частоты интервальных рядов распределения по функциональному и факторному признакам.
Вторая
итоговая строка характеризует сумму
произведений, записанных в верхних
углах клеток. Третья итоговая строка
рассчитывается делением показателей
второй строки на первую. В четвертой
итоговой строке показаны искомые
средние![]() ,
полученные по формуле (5).
,
полученные по формуле (5).
Показатели четвертой итоговой строки являются основой для графического изображения выполненных расчетов на поле корреляции (рис.2).
Таблица 1.9
Расчет эмпирической линии регрессии для зависимости y от x
|
|
|
x |
Потери рабочего времени, чел-часов |
Итого |
|||
|
|
|
y |
249,5 |
262,5 |
275,5 |
288,5 |
|
|
Себестоимость строительно-монтажных работ, тыс.руб. |
-2 |
124,625 |
1 |
2 |
|
1 |
4 |
|
-1 |
141,875 |
2 |
|
1 |
1 |
4 |
|
|
0 |
159,125 |
|
1 |
1 |
|
2 |
|
|
1 |
176,375 |
|
|
|
1 |
1 |
|
|
№ строки |
1 |
Итого hi |
3 |
3 |
2 |
3 |
|
|
2 |
|
-4 |
-4 |
-1 |
-2 |
|
|
|
3 |
|
-1,333 |
-1,333 |
-0,5 |
-0,667 |
|
|
|
4 |
|
136,125 |
136,125 |
150,500 |
147,625 |
|
|
Соединив между собой средние значения в каждом интервале отрезками прямых линий, получаем эмпирическую линию регрессии y по x (см. рис. 2), которая показывает как в среднем изменяется y в связи с изменением x.
В нашем примере расчет эмпирической линии регрессии подтвердил наличие слабой корреляционной зависимости между обеспеченностью материалами и выработкой на 1 рабочего в год.

Рис. 2. Эмпирическая линия регрессии на поле корреляции
1.5. Расчет теоретической линии регрессии
Теоретическая линия регрессии представляет собой такую математически правильную кривую (либо прямую) линию, которая проходит наиболее близко к точкам эмпирической линии регрессии выражает общую закономерность средних изменений признака в связи со средними изменениями фактора.
В
нашем примере характер размещения точек
на корреляционном поле делает весьма
вероятной гипотезу о линейной связи y
от x
![]() .
.
Параметры искомой прямой (а0,а1) находим из системы уравненной по способу наименьших квадратов:
 (7)
(7)
Исходную информацию для решения системы(7) получаем из таблицы 1.10, которая основана на результатах таблицы 1.9.
Для
получения упрощенных вариантов по
факторному признаку также используем
метод отсчета от условного нуля. В нашем
примере примем
![]() =275,5
тыс.руб,
=275,5
тыс.руб,
![]() =332,5
тыс.руб
=332,5
тыс.руб
Результатов расчетов по нашему примеру приведены в таблице1.10.
Таблица 1.10
Расчет теоретической линии регрессии для зависимости y от x
|
Себестоимость строительно-монтажных работ, тыс.руб. |
|
Потери рабочего времени, чел-часов |
№ столбца |
|||||||
|
|
|
4 |
1 |
0 |
1 |
1 |
2 |
3 |
4 |
|
|
|
|
-2 |
-1 |
0 |
1 |
li |
liy` |
y`2 |
liy`2 |
|
|
|
x y |
249,5 |
262,5 |
275,5 |
288,5 |
|||||
|
-2 |
124,625 |
1 |
2 |
|
1 |
4 |
-8 |
4 |
16 |
|
|
-1 |
141,875 |
2 |
|
1 |
1 |
4 |
-4 |
1 |
4 |
|
|
0 |
159,125 |
|
1 |
1 |
|
2 |
0 |
0 |
0 |
|
|
1 |
176,375 |
|
|
|
1 |
1 |
1 |
1 |
1 |
|
|
№ строки |
1 |
Итого
|
3 |
3 |
2 |
3 |
n=11 |
|
- |
|
|
2 |
|
-6 |
-3 |
0 |
3 |
|
||||
|
3 |
|
12 |
3 |
0 |
3 |
|
||||
|
4 |
|
-4 |
-4 |
-1 |
-2 |
|
||||
|
5 |
|
8 |
4 |
0 |
-2 |
|
||||
В качестве проверки правильного составления таблицы 6 должно соблюдаться равенство итогов четвертой строки и второго столбца. Если это условие не соблюдается, то в расчетах допущена ошибка, которая может привести к существенным искажениям величины параметров теоретической линии регрессии.
В систему уравнений (7) подставим результаты, полученные в табл. 1.10.
 (8)
(8)
В качестве метода решения системы (8) принимаем метод Гаусса, который позволяет находить решения последовательно, исключая неизвестные.
Для этого 1-ое уравнение системы (8) делим на 6, а 2-ое уравнение - на 18:
 (9)
(9)
Сложим уравнения системы (9):
1,5![]() =-1,277
=-1,277
откуда
![]() =-0,851.
=-0,851.
Затем
в 1-ое уравнение системы (9) подставляем
значение
![]() и находим величину
и находим величину![]() :
:
1,833![]() (-0,851)-
(-0,851)-![]() =-1,833
=-1,833
![]() =0,273.
=0,273.
Параметры
![]() и
и
![]() необходимо
преобразовать исходя из фактических
значений x и y.
необходимо
преобразовать исходя из фактических
значений x и y.
Формулы перевода из упрощенных в реальные координаты:
![]() (10)
(10)
![]()
![]() (11)
(11)
где
![]() - интервал группировки по функции;
- интервал группировки по функции;
![]() -
интервал группировки по аргументу;
-
интервал группировки по аргументу;
![]() -
новое начало отсчета по функции;
-
новое начало отсчета по функции;
![]() -
новое начало отсчета по аргументу.
-
новое начало отсчета по аргументу.
По формулам (10), (11) находим:
![]() .
.
Уравнение теоретической линии регрессии в реальных коэффициентах имеет вид y=44,603+0,362x.
В уравнении регрессии первое слагаемое носит название свободного члена, второе слагаемое называется коэффициентом регрессии. Он показывает, на сколько натуральных единиц изменяется в среднем результативный признак при изменении факторного признака на единицу.
В нашем примере из уравнения теоретической линии регрессии видно, что себестоимость строительно-монтажных работ увеличивается на 0,362 тыс.руб. при увеличении потерь рабочего времени на 1 чел.-час.
Себестоимость строительно-монтажных работ не зависящая от рассматриваемых факторов, равна 44,603 тыс.руб.
Для графического изображения линии регрессии, рассчитанной по линейной гипотезе, достаточно определить две точки, через которые можно провести прямую.
В нашем примере по x1=243; y1=132,569 и x2=295; y2=151,393 проводим на поле корреляции прямую линию (см. рис. 3)

Рис. 3. Теоретическая линия регрессии на поле корреляции
Графическое изображение теоретической линии регрессии в виде уравнения прямой еще раз подтверждает наличие корреляционной связи между изучаемыми признаками.