
Lesn3_Integraly
.pdf
Глава II. Определенный интеграл
u(x) = g(x) f(x). Очевидно, u(x) 0 на отрезке [a; b]. Тогда
b |
|
|
|
b |
b |
|
b |
|
||
g( x)dx f ( x)dx = |
g(x) f (x) dx = u(x)dx 0 . |
|
||||||||
a |
|
|
|
a |
a |
|
a |
|
||
|
Из этого неравенства следует неравенство (6). |
► |
||||||||
y |
|
|
|
y =g(x) |
|
|
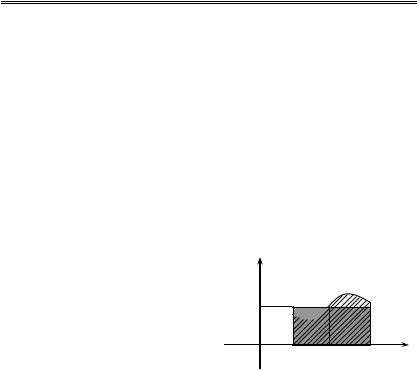
Геометрически: |
|
||
|
|
|
|
если |
0 f(x) g(x) на отрезке |
|||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
[a; b], |
то интеграл от большей |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
функции по этому отрезку дает |
||
|
|
|
|
y = f(x) |
|
|
|
|||
|
|
|
|
|
|
|
площадь большей криволиней- |
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
x |
ной трапеции. |
|
|
O |
a |
|
|
b |
|
|||||
|
|
|
|
|
||||||
Свойство 7 |
(оценка интеграла). Пусть функция f(x) непре- |
|||||||||
|
рывна на отрезке |
[a; b]. Тогда по теореме Вейерштрасса |
||||||||
|
она принимает на [a; b] наименьшее m и наибольшее |
M |
||||||||
|
значения. Имеет место неравенство |
|
||||||||
|
|
b |
|
|
|
m (b a) |
|
f (x)dx |
|
M (b a). |
(7) |
|
|
a |
|
|
|
Доказательство. На отрезке [a; b] функция f(x) удовлетворяет неравенству m f(x) M . По свойству монотонности инте-
|
|
b |
|
b |
|
|
b |
|
грала имеем: m dx |
|
|
f ( x)dx |
Md x. Согласно свойствам |
||||
|
|
a |
|
a |
|
|
a |
|
(2) и (4) из этого неравенства вытекает неравенство (7). |
► |
|||||||
y |
|
|
|
|
|
|
Геометрически: |
|
|
|
|
|
|
если f(x) 0 на отрезке [a; b], |
|||
M |
|
|
|
|
|
|||
|
|
|
|
|
то |
площадь криволинейной |
||
|
|
|
|
|
||||
|
|
|
|
|
|
|||
m |
|
|
|
|
|
трапеции функции f(x) |
больше |
|
|
|
|
|
|
площади вписанного |
прямо- |
||
|
|
|
|
|
|
|||
|
|
|
|
|
x |
угольника, но меньше площади |
||
O |
a |
|
b |
|||||
|
описанного прямоугольника. |
|||||||
|
|
|
|
|
|
|||
Свойство 8 (теорема о среднем значении). Если функция f(x)
непрерывна на отрезке [a; b], то на этом отрезке существует точка x0, для которой выполняется равенство
40
§2. Свойства определенного интеграла
b |
|
|
f ( x)dx |
= f(x0) (b a). |
(8) |
a |
|
|
Доказательство. Так как f(x) непрерывна на отрезке [a; b], то выполняется неравенство (7). Из него вытекает неравенство
|
1 |
b |
|
|
m |
f (x)dx |
M. |
||
b a |
||||
|
a |
|
||
|
|
|
Тогда по теореме о промежуточном значении непрерывной функции следует существование точки x0 [a; b], для которой
1 |
b |
|
|
|
f (x)dx |
= f(x0). Отсюда вытекает равенство (8). |
► |
||
b a |
||||
a |
|
|
||
|
|
|
Геометрически: |
|
Если значения функции |
f(x) |
во всех точках отрезка |
[a; b] |
положить равными f(x0), то площадь криволинейной трапеции функции не изменится.
Число
y
y = f(x)
f(x0) |
|
|
|
O |
a |
b |
x |
|
1 |
b |
|
f(x0) = |
f (x)dx |
||
b a |
|||
|
a |
||
|
|
называется средним значением функции на отрезке [a; b]. Тер-
мин заимствован из физики. Если f(x) – скорость прямолинейного движения некоторого тела на временном промежутке [a; b], то f(x0) есть среднее значение скорости движения данного тела.
Рассмотренные свойства определенного интеграла позволяют решить вопрос о практических способах вычисления этого интеграла.
41
Глава II. Определенный интеграл
Лекция 5
§3. Интеграл с переменным верхним пределом Вычисление определенного интеграла
 усть функция f(x) непрерывна на отрезке [a; b]. Тогда всякому числу x [a; b] можно поставить в соответствие един-
усть функция f(x) непрерывна на отрезке [a; b]. Тогда всякому числу x [a; b] можно поставить в соответствие един-
x
ственное число, равное f (t)dt . Это соответствие является не-
a
которой функцией F(x), определенной на отрезке [a; b] со значениями во множестве всех действительных чисел R:
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
F (x) f (t)dt . |
|
(1) |
||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
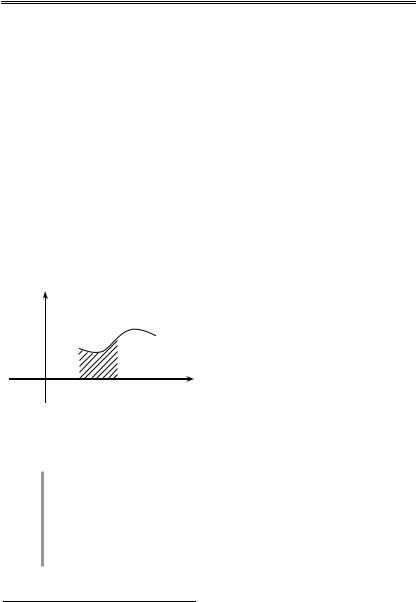
Геометрически: |
|
y |
|
|
|
y = f(x) |
|
если |
f(x) 0 |
на отрезке [a; |
||
|
|
|
|
|
b], |
то значение функции |
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
F(x) |
равно площади криво- |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
линейной трапеции функции |
||
|
|
|
|
|
|
|
||||
|
|
|
F(x) |
|
|
|
|
f(x) на отрезке [a; x]. |
||
|
|
|
|
|
|
|
|
|||
O |
a |
|
x |
|
b x |
Функция, определяемая |
||||
|
|
|
|
|
|
|
|
равенством |
(1), называется |
|
интегралом с переменным верхним пределом. Основное свойство этой функции выражает следующая теорема.
Теорема 1 (Ньютона - Лейбница ).
Интеграл с переменным верхним пределом от непрерывной функции является первообразной для этой функции:
|
x |
' |
|
|
F (x) |
|
|
f (x) . |
|
f (t)dt |
(2) |
|||
|
a |
x |
|
|
Доказательство проведем, используя определение производной.
Ньютон Исаак (1642–1727), английский физик, математик и астроном.Лейбниц Готфрид Вильгельм (1646–1716), немецкий философ, математик, физик, изобретатель, юрист, историк и языковед.
42

§3. Интеграл с переменным верхним пределом
Рассмотрим произвольную точку x (a; b). Придадим аргументу приращение x. Тогда приращение функции F будет равно
|
x x |
x |
a |
x x |
F = F(x + x) F(x) = |
f (t)dt f (t)dt = |
f (t)dt + |
f (t)dt = |
|
|
a |
a |
x |
a |
x x |
|
x x |
|
|
= f (t)dt . Итак, |
F = |
f (t)dt . |
|
|
x |
|
x |
|
|
По теореме о среднем (свойство 8 определенного интеграла) существует точка c [x; x + x], для которой выполняется равенство F = f(c) x. Согласно определению производной имеем:
|
F |
|
f (c) x |
lim f (c) f (x) . |
|
F (x) lim |
|
lim |
|
||
x |
x |
||||
x 0 |
x 0 |
c x |
В случае x = a или x = b аналогичные рассуждения проводятся для соответствующих односторонних производных. ►
 з доказанной теоремы вытекает важное утверждение.
з доказанной теоремы вытекает важное утверждение.
Следствие.
Если функция непрерывна на отрезке, то она имеет на этом отрезке первообразную и, следовательно, неопределенный интеграл.
Следствие дает достаточное условие существования неопределенного интеграла от данной функции и является переформулировкой теоремы 2 из §1 главы 1.
Из равенства f (x)dx = F(x) + C согласно (1) следует, что
f (x)dx = |
x |
|
f (t)dt + C. |
(3) |
a
Это равенство выражает непосредственную связь между неопределенным и определенным интегралами. Теорема 1 является одной из основных теорем математического анализа.
 спользуя теорему 1, получим основной способ вычисления определенного интеграла.
спользуя теорему 1, получим основной способ вычисления определенного интеграла.
43

Глава II. Определенный интеграл
Теорема 2. (Основная теорема интегрального исчисления).
Определенный интеграл от функции f(x), непрерывной на промежутке интегрирования, равен приращению на этом промежутке любой первоóбразной F(x) данной функции:
b |
|
f (x)dx F (b) F (a) . |
(4) |
a
Формула (4) называется формулой Ньютона-Лейбница.
Доказательство. Пусть функция f(x) непрерывна на отрезке [a; b] и F(x) - любая ее первообразная на этом отрезке. Согласно
x
теореме 1 интеграл f (t)dt является одной из первообразных
a
функции f(x). Она отличается от F(x) на некоторую константу:
x |
|
f (t)dt = F(x) + C. |
(*) |
a |
|
При x = a из равенства (*) получаем |
|
a |
|
f (t)dt = F(a) + C = 0. |
|
a |
|
Следовательно, C = F(a). Тогда при x = b из (*) вытекает
b
f (t)dt = F(b) + C = F(b) F(a).
a
Заменив в этом равенстве переменную интегрирования t
на x, получим равенство (4). |
|
► |
Правую часть равенства (4) часто записывают с помощью |
||
знака двойной подстановки: F(b) F(a) = |
F (x)|b . |
|
|
|
a |
Тогда равенство (4) принимает вид: |
|
|
b |
|
|
f (x)dx F (x)|b . |
(4 ) |
|
a |
a |
|
|
|
|
Равенство (4 ) можно, в свою очередь, переписать так:
44

§3. Интеграл с переменным верхним пределом
b |
f (x)dx|b . |
|
f (x)dx = |
(5) |
|
a |
a |
|
|
|
Равенство (5) означает, что вычисление определенного интеграла сводится к вычислению неопределенного с последующей подстановкой пределов интегрирования.
Пример 1.
4 |
4 13 (x 2)3 |
|
4 83 83 5 13 . |
(x 2)2 dx (x 2)2 d (x 2) |
|
||
0 |
0 |
|
0 |
|
|
|
Перейдем к рассмотрению основных методов вычисления определенного интеграла.
§4. Методы вычисления определенного интеграла
Методы вычисления определенного интеграла согласно равенству (5) предыдущего параграфа вытекают из соответствующих методов вычисления неопределенного интеграла.
1. Метод разложения
Пусть функция f(x) представлена (разложена) в виде ли-
|
|
|
n |
нейной комбинации более простых функций: |
f (x) i fi (x) . |
||
|
|
|
i 1 |
Тогда имеет место равенство |
|
|
|
b |
n |
b |
|
f (x)dx |
i fi (x)dx . |
(1) |
|
a |
i 1 |
a |
|
Доказательство вытекает непосредственно из свойств линейности определенного интеграла.
45

Глава II. Определенный интеграл
2. Метод замены переменной (Метод подстановки)
Данный метод основывается на свойстве инвариантности неопределенного интеграла.
b
Теорема 1. Пусть для интеграла f (u(x))d (u(x)) a
выполняются условия:
1)функция u(x) монотонна на отрезке [a; b] и имеет на нем непрерывную производную;
2)u(a) = , u(b) = ;
3)функция f(u) непрерывна на отрезке [ ; ].
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (u(x))d (u(x)) f (u)du . |
|
|
|
|
(2) |
|||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. Из условия 3) следует, что функция |
f(u) имеет |
|||||||||||||||||
на отрезке [ ; ] |
некоторую первообразную F(u) |
и выполняется |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равенство f (u)du F( ) F( ) . |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из условий 1) – 3) следуют также равенства: |
|
|
|
|
|
|||||||||||||
b |
f (u(x))d (u(x)) f (u(x))d (u(x)) |
|
b |
F(u(x))|b |
|
|||||||||||||
|
||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= F(u(b)) F(u(a)) F( ) F( ) . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Итак, оба |
|
интеграла |
|
|
равны |
одному и тому |
же числу |
|||||||||||
F( ) F( ) , то есть имеет место равенство (2). |
|
|
|
|
► |
|||||||||||||
Пример 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||||
|
2 |
|
|
2 |
|
|
|
2 |
|
|
3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||
sin x cos |
|
|
|
|
|
|
u |
du 13 u |
|
|
13 . |
|||||||
|
xdx cos x |
|
|
u |
|
|
|
|
1 |
|||||||||
0 |
|
|
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
46

§3. Интеграл с переменным верхним пределом
Замечание. После выполнения замены переменной в неопределенном интеграле необходимо возвращаться к старой переменной. При вычислении определенного интеграла методом замены в этом нет необходимости.
3. Метод интегрирования по частям
Пусть функции u(x) и v(x) дифференцируемы на отрезке [a; b]. Тогда выполняется равенство
b |
|
b |
|
udv uv|b |
vdu . |
(3) |
|
a |
a |
a |
|
|
|
||
Доказательство. Для неопределенного интеграла справедливо равенство udv uv vdu . Тогда
b |
|
|
udv b |
uv |
|
vdu b |
uv b |
|
|
vdu b |
uv b |
|
b |
|
|
udv |
|
|
|
|
|
|
vdu . ► |
||||||
|
| |
|
| |
| |
|
| |
| |
|
|
|||||
a |
|
|
a |
|
|
a |
a |
|
|
a |
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как и в неопределенном интеграле, равенство (3) позволяет, при подходящем выборе функций u(x) и v(x), перейти от ин-
b |
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
теграла udv |
к более простому интегралу |
vdu . |
|
|
|
||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
Пример 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
u ln x |
|
du x 1dx |
|
|
|
|
e |
e |
|
|
||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 ln xdx |
2 |
|
|
|
|
|
3 |
|
(ln x) |
1 x3 |
|
|
1 x3 x 1dx |
= |
|||
1 |
dv x |
|
dx |
|
v 1 x |
|
|
|
|
3 |
|
1 |
1 |
3 |
|
||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||
= 13 e3 0 13 e x2dx 13 e3 91 x3 |
|
e 13 e3 |
91 e3 |
91 91 (2e3 1) . |
|
||||||||||||
|
|
||||||||||||||||
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Остается заметить, что интегрирование по частям в определенном интеграле применяется в тех же случаях, что и при нахождении неопределенного интеграла.
47

Глава II. Определенный интеграл
§5. Методы приближенного вычисления определенного интеграла
Как уже отмечалось, вычисление определенного интеграла сводится к нахождению неопределенного интеграла (первообразной) и к последующему применению формулы НьютонаЛейбница. В тех случаях, когда неопределенный интеграл вычисляется сложно или он не выражается в элементарных функциях, используется приближенное вычисление определенного интеграла.
Основная идея такого вычисления определенного интеграла заключается в построении интегральных сумм, или их аналогов, без вычисления предела этих сумм. В зависимости от вида строящихся сумм различают несколько методов приближенного вычисления определенного интеграла. Рассмотрим два из них.
1. Метод трапеций
Пусть функция f(x) непрерывна на отрезке [a; b]. Требу-
b
ется приближенно вычислить интеграл f (x)dx .
a
Для наглядности будем предполагать, что f(x) 0 на отрезке [a; b]. В этом случае интеграл равен площади криволинейной трапеции функции f(x) на этом отрезке (см. рис.).
1. Разобьем отрезок [a; b] точками xi на n равных отрезков. Тогда длина отрезков равна x 1n (b a) . Точки разбиения: a = x0, …, xi, ... , xn = b вычисляются по формуле
xi = a + x i, |
i = 0,1,…,n. |
(1) |
2. Вычислим значения функции в этих точках
yi f (xi ) . |
(2) |
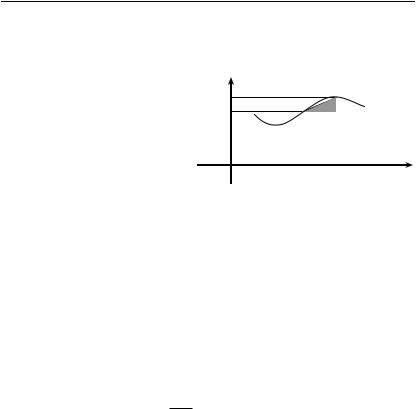
3. Через каждую точку разбиения |
xi проведем параллель- |
48
§5. Методы приближенного вычисления определенного интеграла
но оси |
Oy |
прямую до ее пересечения с графиком функции в |
|||||||||||||||
точке Ai (см. рис). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
На |
отрезке |
[xi 1; xi] |
|
y |
|
|
|
|
|
|
|
|
|
||||
функцию |
f(x) заменим ли- |
|
|
|
|
|
Ai |
|
|
|
|||||||
|
yi |
|
|
|
|
y = f(x) |
|||||||||||
нейной, график которой про- |
|
|
|
|
|
||||||||||||
|
|
|
Ai-1 |
|
|
||||||||||||
ходит через точки |
Ai-1, Ai. |
|
yi-1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
Тогда |
малая |
криволинейная |
|
|
|
|
|
|
|
|
Si |
|
|
|
|
||
трапеция функции |
f(x) на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
отрезке |
[xi 1; xi] |
заменится |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
O a |
xi-1 |
xi b |
x |
|||||||||||||
на обычную трапецию. Пло- |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
щадь |
Si |
малой криволинейной трапеции приближенно равна |
|||||||||||||||
площади обычной трапеции: |
S |
|
1 |
( y |
y ) x . |
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
i |
2 |
|
i 1 |
i |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для площади всей криволинейной трапеции функции |
f(x) |
||||||||||||||||
на отрезке [a; b], то есть для интеграла
b |
n |
n |
||
f (x)dx = Si |
1 |
( yi 1 yi ) x = |
||
2 |
||||
a |
i 1 |
i 1 |
||
b
f (x)dx , имеем равенство a
|
|
n 1 |
|
|
b a |
y0 |
yn 2 yi . |
||
2n |
||||
|
i 1 |
|
||
|
|
|
||
Итак,
b
f (x)dx b a
a
2n
|
n 1 |
y0 yn 2 |
|
|
i 1 |
|
|
yi . (3)
Формула (3) называется формулой трапеций, а рассмотренный метод вычисления интеграла - методом трапеций.
Обозначим через Rn |
разность между левой и правой ча- |
|||||||
стями равенства (3). Пусть |
M 2 |
|
|
|
|
|
|
|
sup | f (x) | , тогда абсолют- |
||||||||
|
|
|
x [a; b] |
|
|
|
||
ная погрешность равенства (3) оценивается неравенством |
|
|
||||||
| R | |
|
(b a)3 |
M |
|
. |
(4) |
||
|
|
2 |
||||||
n |
|
12n2 |
|
|
|
|
||
|
|
|
|
|
|
|
||
Оценка погрешности равенства (3) пропорциональна |
1 |
. |
||||||
|
||||||||
|
|
|
|
|
|
|
n2 |
|
Перейдем к рассмотрению другого метода приближенного вычисления определенного интеграла.
49
