Lesn3_Integraly

Глава III. Дифференциальные уравнения первого порядка

4.Записываем уравнение для C(x): C (x)ex2 2x3ex2 .

5.Решаем это уравнение: C (x) 2x3 ;

C(x) 12 x4 C .

6. Общее решение уравнения (**): u 12 x4ex2 Ce x2 . III. Подставляем функцию u в формулу замены y 2 u :

y 2 12 x4ex2 Cex2 - общий интеграл уравнения (*). Так как = 3 > 1, то имеем дополнительное решение y = 0.

Замечание 2. Уравнение Бернулли

y p(x) y q(x) y

можно решать без замены, используя метод Бернулли, который является обобщением метода Лагранжа.

◄ 1. Записываем однородное уравнение y p(x) y 0 .

2.Его решение (см. решение уравнения (13)) представляем

ввиде y = Cy1, где y1 e p(x)dx .

5. Оно является уравнением с разделяющимися переменными относительно функции C(x) и решается в квадратурах:

6. Найдя общее решение С(x, С1) этого уравнения, записываем общее решение уравнения Бернулли: y C(x,C1 ) y1 . ►

90

§2. Дифференциальные уравнения, интегрируемые в квадратурах

4.Для нахождения функции C(x) записываем уравнение

C ( x) e x22 x3C3 ( x)e x22 3e x2 .

5.Решаем уравнение:

C (x) x3C3 (x) ;

dC( x) x3dx C1 ; C3( x)

Так как = 3 > 1, то имеем особое решение y = 0.

Исследуем теперь еще один вид дифференциальных уравнений первого порядка.

5. Уравнения в полных дифференциалах

Определение 6. Уравнение в симметричной форме p(x, y)dx q(x, y)dy 0

называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции u(x, y) :

91

Глава III. Дифференциальные уравнения первого порядка

Другими словами, уравнение p(x, y)dx q(x, y)dy 0 явля-

ется уравнением в полных дифференциалах тогда и только тогда, когда существует функция u(x, y) , для которой выполняются

равенства (19).

Далее, согласно (18) уравнение в полных дифференциалах

Мы получили, что для решения уравнений в полных дифференциалах достаточно решить две задачи.

1.Определить характеристическое свойство уравнений в полных дифференциалах, по которому можно будет идентифицировать эти уравнения, не решая их.

2.Найти метод определения функции u(x, y) для каждого

такого уравнения.

риступим к решению этих задач.

Определение 7. Множество M R 2 плоскости называется связным, если любые две его точки можно соединить кривой, целиком лежащей во множестве M.

Множество D R 2 называется односвязным, если его граница является связным множеством.

Решение обеих задач нам дает следующее утверждение. Теорема 4. Пусть в уравнении p(x, y)dx q(x, y)dy 0 функции

рывны в односвязной области D 2. В этом случае уравнение является уравнением в полных дифференциалах тогда и только тогда, когда в области D выполняется равенство

Доказательство.

92

§2. Дифференциальные уравнения, интегрируемые в квадратурах

дифференциалах. Тогда существует функция u(x, y) , для кото-

рой выполняются равенства (19). Докажем, что имеет место равенство (21).

Дифференцируя равенства (19) по y и по x соответствен-

Пусть в односвязной области D выполняется равенство (21). Докажем, что уравнение является уравнением в полных дифференциалах. Для этого найдем функцию u(x, y) , которая

где интеграл вычисляется в предположении, что y является константой, C(y) - некоторая функция переменной y.

Найдем C(y). Продифференцируем равенство (*) по y:

Если функция в правой части равенства зависит от x, то равенство будет неверным. Покажем, что данная функция не зависит от x. Для этого докажем, что частная производная по x от функции равна нулю.

Последняя разность равна 0 согласно равенству (21).

93

Глава III. Дифференциальные уравнения первого порядка

Правая часть равенства (**) зависит только от y. Интегрируя обе части равенства по y, находим

Итак, найдена функция u(x, y) , для которой выполняется

равенство (21). Поэтому рассматриваемое уравнение является уравнением в полных дифференциалах. ►

оказанная теорема дает

алгоритм решения уравнения в полных дифференциалах.

1.Убеждаемся, что уравнение удовлетворяет условию (21).

2.Согласно равенству (22) находим функцию u(x, y) .

3.В соответствии с равенством (20) записываем общий интеграл уравнения u(x, y) C .

Замечание. Последний интеграл в равенстве (22) обычно не вычисляется, так как он взаимно уничтожается со всеми слагаемыми второго интеграла, содержащими переменную x.

Это следует из того, что сумма данных двух интегралов равна интегралу от функции, зависящей только от переменной y.

Пример 9.

Решим уравнение

(cos(x y) 2)dx (cos(x y) 5)dy 0 .

94

§2. Дифференциальные уравнения, интегрируемые в квадратурах

поэтому уравнение является уравнением в полных дифференциалах. 2. Найдем функцию u(x, y) согласно равенству (22):

u(x, y) (cos( x y) 2)dx (cos( x y) 5)dy (...); u(x, y) (sin(x y) 2x) (sin(x y) 5y) (...);

u(x, y) sin(x y) 2x 5y .

Для проверки правильности нахождения функции u(x, y) достаточно проверить выполнение равенств (19).

3. Запишем согласно равенству (20) общий интеграл дифференциального уравнения:

sin(x y) 2x 5y С .

Перейдем к рассмотрению численного решения дифференциальных уравнений первого порядка.

§3. Численное решение дифференциальных уравнений первого порядка

Рассмотрим дифференциальное уравнение вида

При решении прикладных задач такие уравнения часто рассматриваются при наличии некоторых экспериментальных данных. Эти данные можно представить как начальные условия задачи Коши для дифференциального уравнения:

В тех случаях, когда решение задачи Коши (1) - (2) не удается найти в аналитическом виде, используют численное решение этой задачи Коши. Такое решение представляет собой построение таблицы приближенных значений функции, являющейся решением задачи Коши.

95

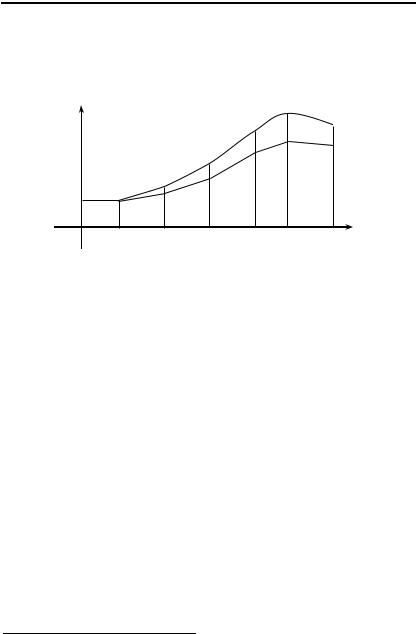
Глава III. Дифференциальные уравнения первого порядка

ассмотрим решение задачи Коши для дифференциально-

го уравнения (1) методом Эйлера .

y(x0 ) y0 . Из равенства (1) следует, что y (x0 ) f (x0 , y0 ) . Рассмотрим точку x1. Она принадлежит малой окрестности

точки x0. Используя свойства дифференциала функции, получаем приближенное значение функции y(x) в точке x1:

Из равенства (1) получаем приближенное значение производной в точке x1: y (x1) f (x1, y1) .

Выполним теперь такие же вычисления для точки x2:

Проделаем аналогичную процедуру последовательно для всех точек xi. В итоге получим приближенные значения функ-

Эйлер Леонард (1707-1783), швейцарский математик, физик, механик.

96

§3. Численное решение дифференциальных уравнений

ции y(x) во всех этих точках. Результаты занесем в таблицу.

а приближенные значения функции yi y(xi ) - по формуле

геометрической точки зрения основа метода Гаусса заключается в следующем. Пусть L - интегральная кривая уравне-

ния (1).

Рассмотрим точку M0(x0; y0) L. Угловой коэффициент k касательной к кривой L в точке M0 определяется, согласно геометрическому смыслу дифференциального уравнения, равенством k y (x0 ) f (x0 , y0 ) . Уравнение этой касательной:

y y0 f (x0 , y0 ) (x x0 ) .

Построим касательную и ее точку пересечения M1 с пря-

состоящей из отрезков касательных к интегральной кривой в соответствующих точках этой кривой.

Заметим, что рассмотренный метод обладает большой погрешностью. Поэтому разработаны многочисленные методы, дающие более точные результаты.

На этом мы закончим исследование дифференциальных уравнений первого порядка. Перейдем к рассмотрению дифференциальных уравнений высших порядков.

97

Глава IV. Дифференциальные уравнения высших порядков

Лекция 11

Глава IV.

Дифференциальные уравнения высших порядков

§ 1. Основные понятия

Начнем исследование дифференциальных уравнений высших порядков. Основные понятия будут аналогичны понятиям из теории дифференциальных уравнений первого порядка. Поэтому ограничимся краткой сводкой этих понятий.

Уже определены дифференциальное уравнение порядка п

F(x, y, y ,..., y(n) ) 0 ,

уравнение, разрешенное относительно старшей производной

Определены понятия решения и интегральной кривой

дифференциального уравнения.

Понятие начального условия для дифференциальных уравнений высших порядков несколько усложняется.

Определение 1. Говорят, что решение y(x) дифференциального уравнения (1) удовлетворяет начальному условию в

точке M(x0, y0, y0 ,…, y0(n-1)) D, если выполняются равенства

Сама система равенств (2) называется начальным условием дифференциального уравнения.

98

§1. Основные понятия

Задача Коши определяется по-прежнему: нахождение решения y(x) дифференциального уравнения (1), удовлетворяющего заданному начальному условию (2).

ля дифференциальных уравнений высшего порядка задача Коши имеет следующее решение.

Теорема Коши (Теорема существования и единственности).

Пусть в дифференциальном уравнении (1) функция

для любой точки (x0, y0, y0,…, y0(n-1)) D существует единственное решение y(x) уравнения, удовлетворяющее начальному условию (2). Решение определено на некотором интервале, содержащем точку x0.

Доказательство опускаем.

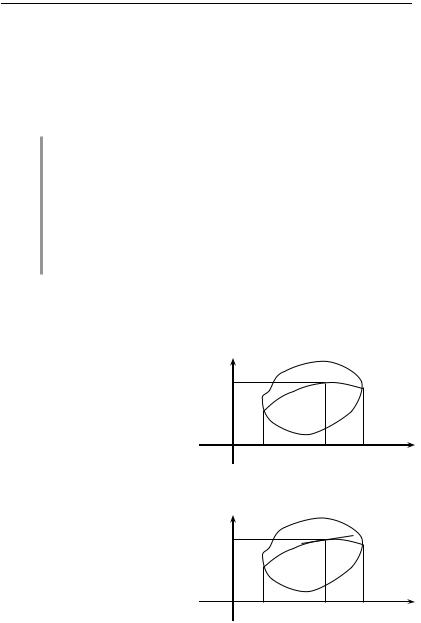
Отметим геометрическую иллюстрацию теоремы Коши.

99