
Lesn3_Integraly1
.pdf
Глава VI. Интегрирование функций нескольких переменных
точки из Mi–1 в Mi будет приближенно равна скалярному про- |
||||||||||
изведению |
|
|
(Ni ), |
|
|
. Для работы |
A по всей кривой CD |
|||
|
Mi 1Mi |
|||||||||
F |
||||||||||
получаем приближенное равенство |
|
|||||||||
|
|
|
|
n |
|
|
|
|||
|
|
|
A |
F |
(Ni ), Mi 1Mi . |
(*) |
||||
|
|
|
|
i 1 |
|
|||||
Это равенство будет тем точнее, чем меньше будет диаметр d разбиения кривой L.
4. Будем последовательно разбивать кривую CD так, чтобы диаметр d разбиения кривой стремился к нулю. Переходя в равенстве (*) к пределу при d 0, получим точное значение
работы силы F по пути CD:
n |
|
|
|
||
A lim |
F |
(Ni ), Mi 1Mi . |
(**) |
||
d 0 i 1 |
|
||||
Задача решена? Строго говоря - нет! Но из области физики |
|||||
она перенесена в область анализа! |
► |
||||
 еперь становится ясным, как будет определен криволинейный интеграл II рода.
еперь становится ясным, как будет определен криволинейный интеграл II рода.
Пусть на направленной плоской кривой AB задана векторная функция F (M ) P(M );Q(M ) . Если M(x; y) AB, то
|
|
(x, y) (P(x, y), Q(x, y)) . |
(1) |
||
|
F |
(M ) |
F |
||
1. Как и при решении задачи о работе силы |
разобьем точ- |
||||
ками M i кривую AB на малые дуги Li. 2. Выберем на них отмеченные точки Ni . 3. Построим сумму вида (*):
Sn n F (Ni ), Mi 1Mi
. i 1
Запишем скалярные произведения векторов в декартовых координатах. Если Ni(xi; yi) AB, то F (Ni ) P(xi , yi ); Q(xi , yi ) .
При переходе от точки Mi–1 к точке Mi координаты точки
получат приращения xi, yi. Поэтому Mi 1Mi ( xi ; yi ) . Тогда сумма Sn примет вид
190

§2. Свойства двойного интеграла
n
Sn P(xi , yi ) xi Q(xi , yi ) yi . (2) i 1
Сумма Sn называется интегральной суммой II рода для векторной функции F (M ) P(x, y);Q(x, y) по кривой AB.
Интегральная сумма еще не дает характеристики векторной функции P(x, y);Q(x, y) на кривой AB. Сумма зависит от
выбора разбиения кривой и от выбора отмеченных точек. Чтобы избавиться от этой зависимости, осуществим предельный переход в интегральной сумме.
4. Будем последовательно разбивать кривую AB так, чтобы диаметр d разбиения стремился к нулю. Как и при определении криволинейного интеграла I рода вводится понятие предела I интегральных сумм при d 0. (Дословное повторение).
Обозначение: |
I lim Sn . |
|
d 0 |
Оказывается, что если предел интегральных сумм существует, то он не зависит от способа разбиения кривой и от выбора отмеченных точек. Поэтому число I полностью определяется векторной функцией P(x, y);Q(x, y) и кривой AB.
Определение 1. Предел интегральных сумм Sn |
при d 0 , если |
|
|
он существует и конечен, называется криволинейным |
|
|
||
|
интегралом II рода векторной функции |
P(x, y);Q(x, y) |
|
по кривой AB. |
|
Обозначение интеграла определяется записью (2) интегральной суммы в координатной форме:
P(x, y)dx Q(x, y)dy .
AB
Используя введенные обозначения, определение интеграла можно записать в символической форме:
|
|
n |
P(x, y)dx Q(x, y)dy = |
lim |
P(xi , yi ) xi Q(xi , yi ) yi . (3) |
AB |
d 0 |
i 1 |
191

Глава VI. Интегрирование функций нескольких переменных
 стественно возникает вопрос о существовании криволинейного интеграла для данных функций.
стественно возникает вопрос о существовании криволинейного интеграла для данных функций.
Теорема 1. (Достаточное условие существования интеграла). Если функции P(x, y) и Q(x, y) непрерывны на плоской кусочно-гладкой кривой AB, то криволинейный интеграл
II рода P(x, y)dx Q(x, y)dy существует.
AB
Доказательство опускаем.
Рассмотрим физический смысл криволинейного интеграла II рода.
Замечание. Если векторная функция P(x, y); Q(x, y) является вектором силы, заданной на плоской кривой CD, то криво-
линейный интеграл II рода P(x, y)dx Q(x, y)dy |
равен |
|||||
|
|
|
|
|
CD |
|
работе этой силы по пути CD: |
|
|||||
|
|
P(x, y)dx Q(x, y)dy A . |
(4) |
|||
|
|
CD |
|
|
||
Утверждение вытекает из решения задачи о работе силы и |
||||||
определения криволинейного интеграла II рода. |
|
|||||
Обратимся к исследованию свойств интеграла. |
|
|||||
2. Свойства криволинейного интеграла II рода |
|
|||||
Начнем с рассмотрения частных ситуаций. |
|
|||||
|
|
|
Q(x, y) 0 и криволинейный интеграл |
|||
Если F (M ) || i , то |
||||||
II рода принимает вид |
P(x, y)dx 0dy . Интеграл равен работе |
|||||
|
|
|
|
AB |
|
|
силы в направлении оси Ox . Для него используется краткая за-
пись P(x, y)dx .
AB
Если F (M ) || j , то интеграл записывается так: Q(x, y)dy .
AB
192

§2. Свойства двойного интеграла
Далее в записи интеграла будем опускать аргументы функций P(x, y), Q(x, y). Первые три свойства интеграла вытекает непосредственно из равенства (3).
Свойство 1. Имеет место равенство
|
Pdx Qdy Pdx Qdy . |
(5) |
|||
|
AB |
|
AB |
AB |
|
Свойство 2. |
Пусть линия |
AB |
является отрезком. Если отрезок |
||
параллелен оси Ox, |
то |
Qdy 0 , если же отрезок парал- |
|||
|
|
|
AB |
|
|
лелен оси Oy, то Pdx 0 . |
|
|
|||
|
AB |
|
|
|
|
Свойство 3. |
При изменении |
направления обхода |
кривой AB |
||
криволинейный интеграл II рода меняет только знак: |
|||||
|
Pdx Qdy Pdx Qdy . |
(6) |
|||
|
BA |
|
AB |
|
|
Свойство 4 (аддитивности). Если C ‒ точка кривой AB, то |
|||||
|
Pdx Qdy = |
Pdx Qdy + Pdx Qdy .(7) |
|||
|
AB |
AC |
|
CB |
|
Для доказательства равенства достаточно рассмотреть интегральные суммы, в которых точка C является точкой разбиения кривой AB.
Рассмотрим особо случай, когда кривая AB является замкнутой, то есть начальная точка A совпадает с конечной точкой B. В этом случае обозначения AB и BA ничего не говорят о направлении обхода кривой. Введем следующие понятия.
Определение 2. Плоская замкнутая кривая без самопересечений называется контуром. Направление обхода контура, при котором внутренняя область, ограниченная этим контуром, все время остается слева по ходу движения, называ-
ется положительным направлением. Противоположное направление обхода контура называется отрицательным.
Обозначения: контур C; внутренняя область DC.
193
Глава VI. Интегрирование функций нескольких переменных
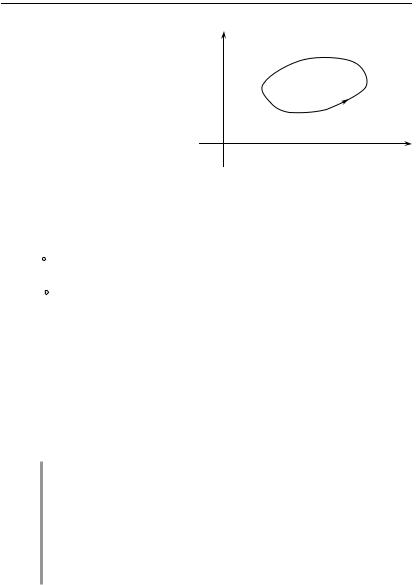
Свойство 5. Криволинейный
интеграл II рода по кон- |
y |
|
|
|
||||
|
|
|
|
|||||
туру не зависит от вы- |
|
|
|
|
||||
бора начальной точки. |
|
|
|
|
|
|||
Действительно, |
|
возь- |
|
|
|
. |
||
мем на контуре точки A, |
A1 |
и |
|
|
|
A |
||
вспомогательные точки M, N |
|
|
|
|
||||
(см. рис.). Имеют место ра- |
O |
|
|
|
||||
венства: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AMA NA |
|
AMA |
A NA |
|
A NA |
|
AMA |
|
1 |
|
|
1 |
1 |
|
1 |
|
1 |
N |
|
. |
. A1 |
|
|
|
DC |
|
. + |
|
M |
x
.
A NAMA
1 1
С учетом последнего свойства криволинейный интеграл II рода по контуру обозначается так:
Pdx Qdy - при положительном направлении обхода;
С
Pdx Qdy - при отрицательном направлении.
С
§10. Вычисление криволинейного интеграла II рода
1. Вычисление в декартовых координатах
Вычисление криволинейного интеграла II рода сводится к вычислению некоторого определенного интеграла.
Теорема 1. Пусть функции P(x, y) и Q(x, y) непрерывны на плоской гладкой кривой AB, заданной параметрически
x = x(t), y = y(t), t [ ; ], = tA, (1)
Тогда выполняется равенство
P(x, y)dx Q(x, y)dy =
AB
|
|
= P(x(t), y(t)) x (t) Q(x(t), y(t)) y (t) dt . |
(2) |
|
|
Доказательство. Воспользуемся первым свойством интеграла и рассмотрим сначала интеграл P(x, y)dx .
AB
194
§2. Свойства двойного интеграла
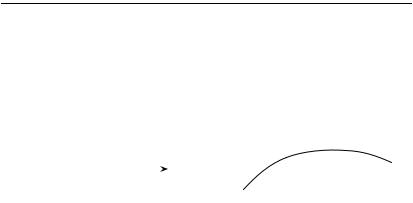
Данный интеграл, как предел интегральных сумм, не зависит от выбора разбиения кривой и выбора отмеченных точек. Построим следующую интегральную сумму функции P(x, y).
1. Разобьем отрезок [ ; ] на n малых отрезков точками ti. Обозначим ti = ti ti 1. Соответствующие точки Mi(x(ti), y(ti)) разобьют кривую AB на n малых дуг.
|
|
|
|
|
Ni |
. |
|
|
|
|
τ.i . |
|
. |
. |
. |
||
. |
. |
. |
|
Mi |
||||
Mi–1 |
||||||||
|
ti–1 |
ti |
β |
|
B |
|||
.A |
|
|
|
|||||
|
|
|
|
|
|
|
||
На отрезке [ti 1;ti ] рассмотрим функцию x(t). По условию она дифференцируема на этом отрезке. По теореме Лагранжа (I семестр) существует точка i [ti 1;ti ] , для которой выполняется равенство xi x(ti ) x(ti 1) x ( i ) ti .
2.Пусть xi x( i ), yi y( i ) . Возьмем в качестве отмеченной точки Ni (xi , yi ) Mi 1Mi .
3.Составим интегральную сумму II рода для функции P(x, y) по кривой AB:
n |
n |
P(xi , yi ) xi P(x( i ), y( i ))x ( i ) ti . |
|
i 1 |
i 1 |
В правой части равенства находится интегральная сумма функции P(x(t), y(t)) x (t) переменной t на отрезке [ ; ].
4. Переходя в данном равенстве к пределу при |
d 0, по- |
|
лучим равенство интегралов |
|
|
|
|
|
P(x, y)dx = P(x(t), y(t)) x (t)dt . |
|
|
AB |
|
|
Аналогично доказывается равенство |
|
|
|
|
|
Q(x, y)dy = Q(x(t), y(t)) y (t)dt . |
|
|
AB |
|
|
Согласно первому свойству криволинейного интеграла II |
||
рода из этих равенств вытекает равенство (9). |
► |
|
195
Глава VI. Интегрирование функций нескольких переменных
Следствие. Пусть функции P(x, y) и Q(x, y) непрерывны на плоской гладкой кривой AB, заданной явно
y = y(x), x [a; b], a = xA, b = xB. |
(3) |
Тогда выполняется равенство
|
b |
|
P(x, y)dx Q(x, y)dy |
= P(x, y(x)) Q(x, y(x)) y (x) dx . (4) |
|
AB |
a |
|
Доказательство. По условию кривую |
AB можно задать пара- |
|
метрически: x = x, y = y(x), x [a; b]. |
Параметром t является |
|
переменная x. Тогда равенство (4) следует из равенства (2).
Замечание. Имеет место равенство, двойственное равенству (4). Пусть функции P(x, y) и Q(x, y) непрерывны на плоской гладкой кривой AB, заданной явно
x = x(y), |
y [a; b], c = yA, d = yB. |
(3') |
|
Тогда выполняется равенство |
|
||
P(x, y)dx Q(x, y)dy |
d |
P(x( y), y) x ( y) Q(x( y), y) dy . (4') |
|
= |
|||
AB |
c |
|
|
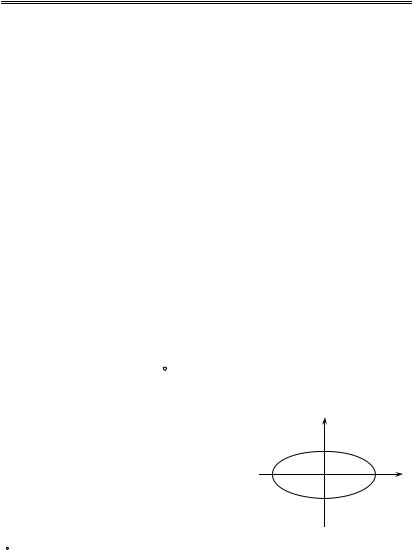
Пример 1.
Вычислим интеграл ( y)dx xdy ,
C |
|
где C - эллипс: x a cost, |
y bsin t . |
Контур задан параметрически, поэтому воспользуемся равенством (2).
Возьмем в |
качестве начальной точку |
A(a, 0). Тогда |
t A 0 , tB 2 . |
Найдем производные:
x (t) a sint , y (t) bcost .
Согласно равенству (2) получаем:
y b
|
A |
O |
a x |
|
2 |
|
2 |
|
( y)dx xdy = |
|
( bsint)( a sint) a cost b cost dt |
= |
ab (sin2 t cos2 t)dt = |
C |
0 |
|
|
0 |
2 |
|
|
|
|
= ab dt 2 ab .
0
Перейдем к исследованию криволинейного интеграла II рода в двух частных случаях.
196
§2. Свойства двойного интеграла
2. Криволинейный интеграл II рода по контуру. Формула Грина
Рассмотрим сначала криволинейный интеграл II рода по кривой особого вида – по контуру.
Теорема 2. Пусть плоская замкнутая |
область |
DC ограничена |
|||||
|
кусочно-гладким контуром C. Функции |
P(x, y), |
Q(x, y) |
||||
|
|||||||
|
имеют в области DC |
непрерывные частные производные |
|||||
|
первого порядка. Тогда выполняется равенство |
|
|||||
|
|
|
Q |
|
P |
|
(5) |
|
Pdx Qdy |
x |
|
dxdy . |
|||
|
С |
|
|
y |
|
|
|
|
DC |
|
|
|
|
|
|
|
|
|
|
|
|
||
Равенство (5) называется формулой Грина .
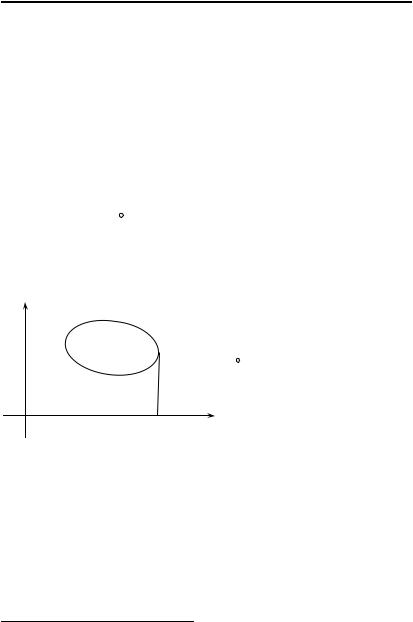
Доказательство рассмотрим для случая, когда область DC явля-
|
|
|
|
|
|
y = H(x) |
|
|
ется простой как по верти- |
||||||
y |
|
|
|
|
M. |
|
|
кали, так и по горизонтали. |
|||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
A |
|
. |
|
.B |
|
|
Докажем сначала равенство |
|||||
|
|
|
|
DC |
|
|
|
|
|
P |
|
||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Pdx |
dxdy . (*) |
|||||
|
|
|
|
|
M |
|
|
|
|
С |
|
|
y |
|
|
|
|
|
|
|
y = h(x) |
|
|
DC |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Пусть |
|
область |
DC |
|
O |
|
|
a |
|
b |
x |
проецируется |
параллельно |
|||||||
|
|
|
оси Oy на отрезок |
[a; b] |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
оси |
|
Ox. Нижняя граница |
y = h(x) |
и верхняя граница y = H(x) |
|||||||||||
области образуют контур C = AMBNA (см. рис.). |
|
|
|
||||||||||||
|
|
|
Преобразуем двойной интеграл: |
|
|
|
|
|
|||||||
|
|
P |
b |
H (x) P(x, y) |
|
b |
|
|
|
H (x) |
|||||
|
|
|
|
|
|
||||||||||
|
|
|
dxdy = dx |
|
y |
dy = |
P(x, y) (x) |
h(x) |
dx = |
||||||
|
|
y |
a |
h(x) |
|
a |
|
|
|
|
|
||||
DC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
b |
|
|
b |
|
|
|
|
= |
P(x, H (x)) P(x, h(x)) dx = P(x, h(x))dx P(x, H (x))dx = |
||||||||||||||
|
a |
|
|
|
|
|
|
a |
|
|
a |
|
|
|
|
Грин, Джордж (1793 – 1841), английский математик и физик.
197

Глава VI. Интегрирование функций нескольких переменных
= P(x, y)dx |
P(x, y)dx |
Pdx |
Pdx Pdx . |
|
AMB |
ANB |
AMB |
BNA |
C |
Итак, равенство (*) выполняется. Аналогичными рассуждениями доказывается равенство
Qdy |
Q |
dxdy . |
|
||||
|
|
|
|||||
С |
DC |
x |
|
||||
|
|
|
|
||||
Складывая эти равенства, получаем равенство (5). |
► |
||||||
Следствие. Если плоская область |
|
D ограничена кусочно-глад- |
|||||
ким контуром C, то имеют место равенства: |
|
||||||
SD xdy ydx |
1 |
( y)dx xdy . |
(6) |
||||
2 |
|||||||
C |
C |
|
C |
|
|||
Доказательство вытекает из формулы Грина и свойства двойного интеграла SD 1dxdy.
D
3. Криволинейный интеграл II рода, независящий от формы пути интегрирования
Пусть функции P(x, y), Q(x, y) определены в некоторой области D R 2 . Возьмем произвольные точки A, B из этой области и соединим их некоторой кривой L.
Рассмотрим криволинейный интеграл II рода
P(x, y)dx Q(x, y)dy .
L
Если брать другие кривые, соединяющие точки A и B, то интеграл будет принимать, вообще говоря, различные значения. Однако в некоторых случаях интеграл ведет себя совершенно подругому - он не изменяет своих значений.
Определение 1. Криволинейный интеграл II рода называется
независящим от формы пути интегрирования в обла-
сти D, если для любых точек A, B D значение интеграла не зависит от выбора в области D кусочно-гладкой кривой, соединяющей точки A и B.
198

|
§2. Свойства двойного интеграла |
Обозначения интеграла: |
|
B |
(x1, y1 ) |
Pdx Qdy , |
P(x, y)dx Q(x, y)dy . |
A |
(x0 , y0 ) |
◄ Исследуем, как можно вычислять криволинейный интеграл, независящий от формы пути интегрирования, учитывая его особенность. Рассмотрим интеграл
(x1, y1 )
P(x, y)dx Q(x, y)dy .
(x0 , y0 )
y
y0
O
В качестве кривой, соединяющей точки A(x0, y0) и B(x1, y1),
|
|
|
|
возьмем ломаную, состо- |
|
|
|
.B(x1,y1) |
ящую из двух отрезков, |
||
|
|
||||
|
|
|
|
параллельных |
осям ко- |
|
|
|
|
ординат (см. рис.). Коор- |
|
. |
|
.С(x1,y0) |
динаты точки C извест- |
||
A(x0,y0) |
|
ны: C(x1, y0). |
|
||
|
|
|
Согласно |
свой- |
|
|
|
|
|
||
|
x1 |
x |
ствам интеграла имеем: |
||
|
|
|
|||
(x1, y1 ) |
C |
B |
C |
B |
Pdx Qdy = Pdx Qdy |
+ Pdx Qdy = |
Pdx + |
Qdy . (*) |
|
(x0 , y0 ) |
A |
C |
A |
C |
Для первого интеграла путь интегрирования AC можно |
||||
задать явно: y = y(x) y0 , |
a = x0, b = x1. Применим вычисли- |
|||
тельную формулу (11): |
|
|
|
|
C |
x1 |
x1 |
|
|
Pdx = P(x, y(x))dx = P(x, y0 )dx . |
|
|||
A |
x0 |
x0 |
|
|
Проведя аналогичные рассуждения для второго интеграла, и используя двойственную формулу (11 ), получим равенство
B |
y1 |
Qdy = Q(x1, y)dy . |
|
C |
y0 |
199
