
Теория вероятностей
.pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования žКузбасский государственный технический университет имени Т. Ф. Горбачева¤
Кафедра математики
МАТЕМАТИКА
Методические указания и задания для контрольной работы № 3 для студентов 2 курса (3 семестр) направлений 190601.62 žАвтомобили и автомобильное хозяйство¤, 151901.62 žТехнология машиностроения¤ и 270800.62 žСтроительство¤ профилей: 270801.62, 270804.62 и 270815.62 заочной формы обучения
Составители Т. С. Жирнова В. М. Волков
Утверждены на заседании кафедры Протокол № 7 от 16.05.2013 Рекомендованы к печати учебно-методической комиссией по направлению 190601.62 Протокол № 14 от 17.05.2013 Электронная копия находится в библиотеке КузГТУ
Кемерово 2013
1
Контрольная работа № 3 составлена в соответствии с программой курса žМатематика¤ для студентов 2 курса (3 семестр) направлений подготовки бакалавров 190601.62 žАвтомобили и автомобильное хозяйство¤, 151901.62 žТехнология машиностроения¤ и 270800.62 žСтроительство¤ профилей: 270801.62 žПромышленное и гражданское строительство¤, 270804.62 žВодоснабжение и водоотведение¤ и 270815.62 žАвтомобильные дороги¤ заочной формы обучения
Номера задач контрольной работы студент должен выбрать по таблице žВыбор номеров контрольных задач¤ следующим образом:
найти строку, соответствующую первой букве фамилии;
найти столбец, соответствующий последней цифре шифра;
на пересечении найденных строки и столбца взять номера задач контрольной работы № 3.
Контрольная работа, выполненная не по своему варианту, возвращается непроверенной.
Таблица 1
Первая |
|
|
|
Последняя цифра шифра |
|
|
|
||||
буква |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
||
фами- |
|||||||||||
лии |
|
|
|
|
|
|
|
|
|
|
|
А З |
1 27 |
14 25 |
5 22 |
14 21 |
5 28 |
11 21 |
1 30 |
5 23 |
8 19 |
10 16 |
|
И Ц |
31 49 |
32 57 |
33 50 |
34 58 |
35 51 |
36 59 |
37 52 |
38 60 |
39 53 |
40 46 |
|
Ч Б |
8 26 |
2 23 |
15 20 |
6 29 |
15 22 |
6 16 |
12 24 |
2 17 |
6 17 |
9 25 |
|
П Р |
41 50 |
42 58 |
43 51 |
44 59 |
45 52 |
31 60 |
32 53 |
33 46 |
33 54 |
35 47 |
|
Э С |
14 24 |
9 19 |
3 30 |
1 24 |
7 17 |
1 25 |
7 18 |
13 18 |
3 24 |
7 26 |
|
В К |
36 51 |
37 59 |
36 52 |
39 60 |
40 53 |
41 46 |
42 54 |
43 47 |
44 55 |
45 48 |
|
Л Т |
4 18 |
15 16 |
10 24 |
14 18 |
12 26 |
8 16 |
2 19 |
8 23 |
14 27 |
4 19 |
|
Ш Г |
31 52 |
32 60 |
33 53 |
34 46 |
35 54 |
36 47 |
37 55 |
38 48 |
39 56 |
40 49 |
|
Д М |
8 17 |
5 25 |
1 19 |
2 27 |
5 30 |
3 20 |
9 22 |
3 28 |
9 18 |
15 20 |
|
У Щ |
41 53 |
42 46 |
43 54 |
44 47 |
45 55 |
31 48 |
32 56 |
33 49 |
34 57 |
35 50 |
|
Ю Е |
2 26 |
9 20 |
6 28 |
2 29 |
12 21 |
6 21 |
4 29 |
10 17 |
4 21 |
10 24 |
|
Н Ф |
36 54 |
37 47 |
38 55 |
39 48 |
40 56 |
41 49 |
42 57 |
45 50 |
44 58 |
45 51 |
|
Х Ж |
13 27 |
12 29 |
10 28 |
7 22 |
13 20 |
13 30 |
7 16 |
11 22 |
12 23 |
13 25 |
|
О Я |
31 55 |
32 48 |
33 56 |
34 49 |
35 57 |
36 50 |
37 58 |
38 51 |
39 59 |
40 52 |
|
2
ПРОГРАММА 2 КУРСА (3 СЕМЕСТР)
Рабочая программа дисциплины žМатематика¤ составлена в соответствии с ФГОС ВПО и примерной ООП подготовки бакалавров направлений 190601.62 žАвтомобили и автомобильное хозяйство¤, 270815.62 žАвтомобильные дороги¤ и 151901.62 žТехнология машиностроения¤ заочной формы обучения.
1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА.
1.Элементы комбинаторики. Понятия перестановок, размещений, сочетаний и подсчет их числа.
2.Алгебра событий. Пространство элементарных событий и вероятность. Классическая, геометрическая и статистическая вероятность.
3.Теоремы сложения и умножения вероятностей. Условная вероятность. Полная вероятность и формула Байеса.
4.Дискретные и непрерывные случайные величины и способ их задания. Числовые характеристики случайных величин.
5.Законы распределения вероятностей дискретных и непрерывных случайных величин. Нормальное распределение. Функция надёжности.
6.Задачи математической статистики. Генеральная и выборочная совокупности. Репрезентативность выборки.
7.Вариационный ряд и его характеристики. Эмпирическая функция распределения. Полигон и гистограмма.
8.Точечные оценки параметров распределения. Несмещенность, состоятельность и эффективность оценки. Интервальная оценка параметров распределения.
9.Проверка статистических гипотез.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ ПО ТЕОРИИ ВЕРОЯТНОСТИ
При нахождении вероятностей сложных событий в задачах 1-15 следует пользоваться теоремами сложения, умножения и следствиями из них ([1] гл.2-4; [2] гл. 2).
3
Пример 1. Два стрелка делают по одному выстрелу. Вероятность поражения мишени первым стрелком равна 0,8, а вторым
– 0,7. Найти вероятности попадания в мишень обоими стрелками; поражения мишени хотя бы одним стрелком.
Решение. Пусть событие A – попадание в мишень первым стрелком, B – вторым. Тогда событие C, заключающееся в одновременном поражении мишени обоими стрелками, является произведением событий А и В (С = АÀВ). Эти события происходят независимо друг от друга. Поэтому вероятность их произведения определяется по формуле
P(АÀВ) = Р(А) Р(В) и равна P(С) =Р(АÀВ) = 0,7À0,8 = 0,56. Рассмотрим теперь событие D – поражение цели хотя бы
одним стрелком. Оно заключается в поражении мишени либо первым стрелком, либо вторым, либо обоими вместе. Это событие является суммой исходных событий, т.е. D = А + В. События А и В являются совместными, т.к. могут происходить в одном и том же испытании. Поэтому следует воспользоваться формулой Р(А+В) = Р(А) + Р(В) –Р(АÀВ).
Получим Р(D) = Р(А+В) = 0,7 + 0,8 - 0,7 0,8 = 0,94.
Пример 2. Пластмассовые заготовки для деталей поступают с пресса №1, выпускающего 50% всей продукции, с пресса №2, выпускающего 30%, и с пресса №3, дающего 20%. При этом доля нестандартной продукции у первого пресса 0,10, у второго – 0,05, а у третьего – 0,02. Наудачу взятая заготовка оказалась стандартной. Определить вероятность того, что она поступила с первого пресса.
Решение. Событие А – взятая заготовка стандартная. Она могла быть изготовлена прессом №1 (гипотеза Н1), прессом №2 (гипотеза Н2) или прессом №3 – Н3. Вероятности этих гипотез соответственно равны Р(Н1)=0,5; Р(Н2)=0,3; Р(Н3)=0,2. Событие А может произойти с событием Н1 с условной вероятностью PH1 (A) 1- 0,1 0,9 . Аналогично имеем условные вероятности:
PH2 |
A 1 0,05 0,95; |
PH3 A 1 |
0,02 0,98. |
Тогда |
полная вероятность |
события А, |
определяемая по |
формуле

4
3
P( A) P(H j ) PHj ( A),
j 1
равна P( A) 0,5 0,9 0,3 0,95 0,2 0,98 0,931.
Для нахождения вероятности РА(Н2) – того, что заготовка изготовлена первым прессом, при условии, что она стандартная,
применим формулу Байеса: |
|
P(H j ) PH j |
( A) |
|||||
|
|
|
PA (H j ) |
|||||
|
|
|
|
|
, |
|||
|
|
P( A) |
|
|||||
|
|
|
0,5 0,9 |
|
|
|
|
|
получаем P (H |
1 |
) |
|
0,483. |
|
|
||
|
|
|
||||||
A |
0,931 |
|
|
|
|
|
||
|
|
|
|
|
|
|
||
Аналогично можно найти условные вероятности гипотез Н1 и Н3. При этом должно выполняться условие
PA (H1 ) PA (H 2 ) PA (H3 ) 1.
Для решения задач № 16 - 30 следует знать условия, к которым применимы формулы Бернулли, Пуассона, локальная и интегральная теоремы Муавра-Лапласа ([1], гл. 5, 6 Á5; [2], гл. 3, 4 Á1).
Пример 3. Монету подбрасывают 5 раз. Найти вероятность того, что герб выпадет ровно 2 раза.
Решение. Число повторных независимых испытаний – подбрасываний монеты n = 5 – мало. Вероятность выпадения герба в од-
ном испытании p 1 , вероятность противоположного события – 2
выпадения цифры: q 1 p 1 . Тогда вероятность выпадения 2
двух гербов (к = 2) следует определять по формуле Бернулли
|
|
P (к) C к pк qn к : |
|
|
|
|
|
|
||||||||||
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|||
P |
(2) C 2 |
|
|
1 2 |
|
1 |
3 |
5! |
|
|
1 |
|
4 5 |
|
5 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||||||
5 |
5 |
|
|
2 |
|
2 |
|
3! 2! 32 |
|
2 32 16 . |
||||||||
Пример 4. В городе каждая десятая машина – иномарка. За час по центральной улице проезжает 900 машин. Какова вероят-

5
ность того, что иномарки составляют среди них не более 90 машин.
Решение. Число независимых испытаний n = 900 – велико, а
вероятность появления иномарки p |
1 |
не близка к нулю. В |
|
||
10 |
|
|
этих условиях используют приближенные формулы Муавра – Лапласа. Так как нас интересует вероятность появления события не более 90 раз, то применим интегральную формулу P(к1, к2 ) Ф( х2 ) Ф( х1) , получим
P900 ( не более 90) P900 (0,90) P900 (0 k 90) Ф( х2 ) Ф( х1 ),
|
|
к1 |
np |
|
|
|
0 900 |
1 |
|
|
|
|
|
|
|
|
|
90 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
где |
x |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
30, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 |
|
|
npq |
100 |
1 |
|
|
9 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
10 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
к2 np |
|
|
|
90 900 |
1 |
|
|
|
|
|
0 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
0. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||||||||
|
|
|
npq |
|
1 |
|
|
|
9 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
По прил. 1 определим значения функции Лапласа Ф(0) = 0, Ф(–30) = –Ф(30) = – 0,5 (функция Лапласа нечетная Ф(–х) = – Ф(х) и при x > 5 Ф(х) = 0,5).
Итак, Р900(не более 90) = 0 + 0,5 = 0,5.
Пример 5. Учебник издан тиражом 10000 экземпляров. Вероятность его неправильной брошюровки равна 0,0001. Найти вероятность того, что тираж содержит две бракованные книги.
Решение. Так как число испытаний n = 10000 – велико, а вероятность p = 0,0001 близка к нулю, то используем формулу Пуассона. Для этого определим параметр = np = 1 и вычислим
P (2) |
к e |
|
12 e 1 |
|
1 |
0,18. |
|
|
|
||||
10000 |
к! |
2! |
|
2e |
||
|
|
|||||
Закон распределения дискретных случайных величин, их числовые характеристики (задачи № 31 - 45) рассмотрены в гл. 6-8 [1], гл.4 [2], гл.11 [3].

6
При составлении закона распределения случайной величины для нахождения вероятностей возможных значений можно использовать основные теоремы и формулы теории вероятностей.
Пример 6. Рабочий обслуживает два станка. В течение смены первый станок потребует внимания рабочего с вероятностью 0,2, второй – с вероятностью 0,3. Составить закон распределения числа станков, потребовавших внимания рабочего в течение смены. Вычислить его числовые характеристики.
Решение. Дискретная случайная величина Х – число станков, потребовавших внимания рабочего. Обозначим событие Аi –
внимание потребовал i-й станок, тогда, Ai – i-й станок не потребовал внимания рабочего. Итак, Р(А1) = 0,2, P( A1 ) = 1 – Р(А1) =
0,8, Р(А2) = 0,3, P( A2 ) = =1 – Р(А2) = 0,7.
Определим вероятность того, что случайная величина Х
примет возможные значения 0, 1, 2:
P( X 0) P( A1 A2 ) P( A1 ) P( A1) 0,8 0,7 0,56;
P( X 1) P( A1 A2 A1 A2 ) P( A1 A2 ) P( A1 A2 )
P( A1 )P( A2 ) P( A1)P( A2 ) 0,2 0,7 0,8 0,3 0,14 0,24 0,38; P( X 2) P( A1) P( A2 ) 0,2 0,3 0,06.
Составим закон распределения:
Х |
0 |
1 |
2 |
|
|
|
|
Р |
0,56 |
0,38 |
0,06 |
3
Контроль: pi 0,56 0,38 0,06 1.
i 1
Вычислим основные числовые характеристики: математическое ожидание М(Х),
3
М ( Х ) xi pi 0 0,56 1 0,38 2 0,06 0,5,
i 1
дисперсию D(Х) = М(Х2) - (М(Х))2. Для этого составим закон распределения квадрата случайной величины Х:

|
|
7 |
|
|
|
|
|
Х2 |
0 |
1 |
4 |
Р |
0,56 |
0,38 |
0,06 |
М(Х2) = 0À0,56 + 1À0,38 + 4À0,06 = 0,62, D(Х) = 0,62-(0,5)2 = 0,37.
Среднее квадратическое отклонение:
( X ) 
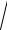 D( Х )
D( Х ) 
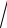 0,37 0,61.
0,37 0,61.
Вряде задач на повторные независимые испытания вычисление вероятностей возможных значений случайной величины и
еечисловых характеристик упрощается.
Пример 7. Каждый из трех независимо работающих приборов регистрирует уровень шума, превышающий установленную норму с вероятностью 0,9. Составить закон распределения числа приборов, зарегистрировавших шум, превышающий норму. Вычислить его числовые характеристики.
Решение. Случайная величина Х – число приборов, зарегистрировавших превышение уровня шума, может принимать четыре значения (к = 0, 1, 2, 3); соответствующие вероятности найдем по формуле Бернулли при n = 3; p = 0,9; q = 1– p = 0,1; к = 0,
1, 2, 3.
P(X = 0) = P3(0) = C30p0q3 = 0,001, P(X = 1) = P3(1) = C31p1q2 = 0,027, P(X = 2) = P3(2) = C32p2q1 = 0,243, P(X = 3) = P3(3) = C33p3q0 = 0,729.
Запишем закон распределения случайной величины:
0 |
1 |
2 |
3 |
0,001 |
0,027 |
0,243 |
0,729 |
3
Контроль: pi 0,01 0,027 0,243 0,729 1.
i 1
Закон распределения составлен правильно.
Так как случайная величина имеет биномиальный закон распределения, то математическое ожидание
8
М(Х) = nÀp = 3À0,9 = 2,7.
Дисперсия D(Х) = npq = 4À0,9À0,1 = 0,36 и среднее квадратическое отклонение ( X ) 
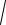 D( Х ) 0,6.
D( Х ) 0,6.
Особую трудность у студентов вызывает составление закона распределения. Поясним этот процесс еще на одном примере.
Пример 8. На пути движения автомобиля 3 светофора. Каждый из них с вероятностью 0,6 разрешает автомобилю дальнейшее движение. Найти закон распределения числа светофоров, пройденных автомобилем до первой остановки.
Решение. Здесь случайной величиной Х является число светофоров, пройденных автомобилем до первой остановки.
Пусть событие А – светофор пройден без остановки, A – противоположное событие (остановка).
Вычислим вероятность значений случайной величины: P( X 0) P( A) 1 P( A) 0,4,
P( X 1) P( A A) 0,6 0,4 0,24,
P( X 2) P( A A A) 0,6 0,6 0,4 0,144,
P( X 3) P( A A A) 0,6 0,6 0,6 0,216.
3
Контроль: pi 0,4 0,24 0,144 0,216 1.
i 1
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ ПО МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ
Задача 1. Построение вариационного ряда, вычисление выборочных характеристик вариационного ряда и подбор теоретического закона распределения.
Теоретический материал, необходимый для выполнения задания, изложен в [1, гл. 15–17; 2, гл. 10; 4].
Пример 1. На угольных предприятиях исследовали производительность труда рабочих при проходке штрека (случайная величина Х). Результаты наблюдений приведены в табл. 2.

9
По выборке случайной величины Х требуется: а) построить интервальный вариационный ряд;
б) по сгруппированной выборке вычислить выборочное среднее x , выборочную дисперсию S x2 и выборочное среднее квадратическое отклонение Sx ;
в) построить гистограмму вариационного ряда; г) проверить гипотезу о нормальном распределении случай-
ной величины X по критерию Пирсона при уровне значимости0,05.
Таблица 2
№ |
Х |
№ |
Х |
№ |
Х |
№ |
Х |
№ |
Х |
|
|
|
|
|
|
|
|
|
|
1 |
0,32 |
11 |
0,19 |
21 |
0,16 |
31 |
0,15 |
41 |
0,15 |
2 |
0,16 |
12 |
0,16 |
22 |
0,33 |
32 |
0,18 |
42 |
0,19 |
3 |
0,27 |
13 |
0,14 |
23 |
0,23 |
33 |
0,21 |
43 |
0,31 |
4 |
0,25 |
14 |
0,27 |
24 |
0,35 |
34 |
0,26 |
44 |
0,22 |
5 |
0,29 |
15 |
0,18 |
25 |
0,20 |
35 |
0,27 |
45 |
0,23 |
6 |
0,17 |
16 |
0,24 |
26 |
0,17 |
36 |
0,22 |
46 |
0,36 |
7 |
0,18 |
17 |
0,12 |
27 |
0,25 |
37 |
0,23 |
47 |
0,31 |
8 |
0,22 |
18 |
0,24 |
28 |
0,20 |
38 |
0,16 |
48 |
0,21 |
9 |
0,29 |
19 |
0,21 |
29 |
0,18 |
39 |
0,18 |
49 |
0,16 |
10 |
0,25 |
20 |
0,23 |
30 |
0,17 |
40 |
0,17 |
50 |
0,28 |
Решение. Для построения интервального вариационного ряда найдем по формуле Стерджеса оптимальную ширину интервала (шаг)
h xmax xmin ,
1 3,2 lg n
где xmax , xmin – соответственно наибольшее и наименьшее значения признака Х; n – объем выборки. В табл. 2 находим
xmax 0,36 ; xmin 0,12 ; n 50 . Тогда
h |
|
0,36 0,12 |
|
0,24 |
0,037 0,04 . |
1 3,2 lg 50 |
|
||||
|
6,44 |
|
|||
