
Теория вероятностей
.pdf10
При этом шаг рассчитываем с той же точностью, с которой
заданы исходные данные. |
|
|
|
Определим границы интервалов |
|
|
|
[l0 , l1 ), [l1, l2 ), ..., [lk 1, lk ], |
|
где |
l0 xmin 0,12; |
l1 l0 h 0,12 0,04 0,16; ..., lk |
lk 1 |
h |
и так до тех пор, пока |
xmax 0,36 не попадет в последний интервал.
Составим интервальный вариационный ряд (табл. 3).
|
|
|
Таблица 3 |
|
|
|
|
№ |
Интервалы |
Частота mi |
Относительная частота рi |
|
|
|
|
1 |
2 |
3 |
4 |
1 |
0,12 – 0,16 |
4 |
0,08 |
2 |
0,16 – 0,20 |
16 |
0,32 |
3 |
0,20 – 0,24 |
14 |
0,28 |
4 |
0,24 – 0,28 |
8 |
0,16 |
5 |
0,28 – 0,32 |
5 |
0,10 |
6 |
0,32 – 0,36 |
3 |
0,06 |
|
Сумма |
50 |
1 |
Частота mi – число значений признака Х, попадающих в i-й интервал [li 1, li ) (столбец 3). При этом сумма частот должна равняться объему выборки, mi n.
i
Относительная частота p |
mi |
попадания в i-й интервал |
|
||
i |
n |
|
|
|
служит оценкой вероятности того, что признак Х примет значение, принадлежащее i-му интервалу (столбец 4). Их сумма долж-
на быть равна единице: pi |
1. |
|
|||||||||
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
Для вычисления выборочных характеристик составим рас- |
||||||||
четную табл. 4. |
|
|
|
|
|
|
|||||
|
|
|
Во |
2-м столбце табл. |
4 |
записаны середины |
интервалов |
||||
x |
i |
|
li 1 |
li |
. Например, |
x |
|
1 |
0,12 1,16 0,14 |
– середина |
|
|
|
|
|||||||||
|
2 |
|
|
1 |
2 |
|
|
||||
|
|
|
|
|
|
|
|||||
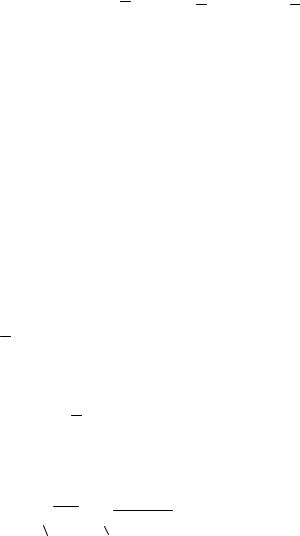
11
первого интервала.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
№ |
xi |
mi |
|
xi mi |
|
|
xi |
x |
|
|
|
(xi |
x |
)2 |
(xi |
x |
)2 mi |
|
||||||
|
1 |
2 |
3 |
4 |
|
|
|
5 |
|
|
|
|
6 |
|
|
7 |
|
||||||||
|
1 |
0,14 |
4 |
0,56 |
|
-0,08 |
|
|
0,0064 |
0,0256 |
|
||||||||||||||
|
2 |
0,18 |
16 |
2,88 |
|
-0,04 |
|
|
0,0016 |
0,0256 |
|
||||||||||||||
|
3 |
0,22 |
14 |
3,08 |
|
0 |
|
|
|
|
0 |
|
|
0 |
|
||||||||||
|
4 |
0,26 |
8 |
2,08 |
|
0,04 |
|
|
0,0016 |
0,0128 |
|
||||||||||||||
|
5 |
0,30 |
5 |
1,50 |
|
0,08 |
|
|
0,0064 |
0,0320 |
|
||||||||||||||
|
6 |
0,34 |
3 |
1,01 |
|
0,12 |
|
|
0,0144 |
0,0432 |
|
||||||||||||||
|
Сумма |
|
50 |
11,11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1392 |
|
||||||
|
Рассчитаем числовые характеристики интервального ряда. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
6 |
|
|
mi |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
xi |
|
11,11 |
|
|
|
|
|
|
|
||||||||||
Выборочное среднее |
x |
|
i 1 |
|
|
|
|
0,22 . |
|||||||||||||||||
|
|
|
|
50 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Выборочная дисперсия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
6 |
|
|
|
|
|
)2 m |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
( x |
i |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Sx2 |
i 1 |
|
|
|
|
i |
|
0,1392 |
0,0028. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
||||||
Выборочное среднее квадратическое отклонение Sx 
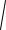 Sx2
Sx2 
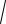 0,0028 0,053.
0,0028 0,053.
По данным интервального ряда (табл. 3) построим гистограмму (рис. 1). По оси OX откладываем интервалы, по оси OY – соответствующие им частоты.

|
|
|
|
12 |
|
|
mi |
|
|
|
|
|
|
16 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
0 |
0,16 |
0,20 |
0,24 |
0,28 |
0,32 |
X |
0,12 |
0,36 |
|||||
Рис. 1. Распределение производительности труда рабочих |
||||||
По виду гистограммы предполагаем, что производительность труда Х распределена по нормальному закону. Кроме того, проверим, удовлетворяют ли выборочные числовые характеристики особенностям этого распределения:
xmax xmin |
|
x |
, |
xmax xmin |
S x . |
|
2 |
6 |
|||||
|
|
|
|
Имеем, во-первых:
xmax xmin |
|
0,12 |
0,36 |
0,24 , |
2 |
|
|
||
2 |
|
|
||
что близко к x 0,22; и, во-вторых,
xmax xmin |
|
0,36 0,12 |
0,04 |
, |
6 |
|
|||
6 |
|
|
||
что близко к Sx 0,053. Таким образом, оценка найденных параметров не противоречит сделанному предположению о виде распределения. Функция плотности вероятности нормального распределения имеет два параметра a и , которые равны a x 0,22 , Sx 0,053:
|
|
1 |
|
|
( x a)2 |
|
||
|
|
|
|
2 . |
||||
f (x) |
|
|
e 2 |
|||||
|
|
|
|
|||||
|
2 |
|||||||
|
|
|
|
|
|
|
||
Итак, функция плотности вероятности теоретического закона распределения имеет вид
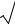
|
13 |
|
|
|
|
|
|
|
1 |
|
|
|
( x 0,22) 2 |
||
|
|
|
|
2 |
|
||
f (x) |
|
|
e 2 (0,053) |
|
|||
|
|
|
. |
||||
0,053 |
|
|
|||||
|
|||||||
|
2 |
|
|
||||
Для проверки согласованности теоретического и наблюдаемого распределений рассчитаем теоретические частоты. Сначала найдем теоретические вероятности попадания случайной величины в заданные интервалы, используя формулу:
|
Т |
|
a |
|
a |
|
||
р |
|
P( X ) Ф |
|
|
Ф |
|
|
, |
|
|
|
||||||
i |
|
|
|
|
||||
где значения Ф X найдем по прил. 1.
Теоретические частоты будем находить как miТ рiT n , округляя их значения до целых. Результаты вычислений приведены
в табл. 5. |
|
|
Ф 0,38 0,15 |
|
|
|
|
|
|
|
|
|
Таблица 5 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
№ |
Интервал |
|
|
|
|
a |
|
a |
рT |
miТ |
mi |
||||||||||||||
|
|
; |
|
|
Ф |
|
|
|
|
|
|
Ф |
|
|
|
|
|
|
|
i |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
; |
0,16 |
|
Ф 1,13 0,37 |
Ф 0,5 |
0,13 |
6 |
4 |
|||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1,13 |
|
0,22 |
11 |
16 |
||||||||
|
0,16; 0,20 |
|
|
Ф 0,38 |
|
0,15 |
Ф |
|
|
0,37 |
|
|
|
||||||||||||
3 |
|
|
|
|
|
Ф 0,38 |
|
0,15 |
|
0,38 |
|
0,3 |
15 |
14 |
|||||||||||
|
0,20; 0,24 |
|
|
|
|
Ф |
|
0,15 |
|
|
|
||||||||||||||
4 |
|
|
|
|
|
Ф 1,13 |
|
0,37 |
Ф 0,38 |
|
0,15 |
0,22 |
11 |
8 |
|||||||||||
|
0,24; 0,28 |
|
|
|
|
|
|
|
|
||||||||||||||||
5 |
|
|
|
|
|
Ф 1,89 |
|
0,47 |
Ф 1,13 |
|
0,37 |
0,1 |
5 |
5 |
|||||||||||
|
0,28; 0,32 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
6 |
|
0,32; |
|
|
|
|
0,5 |
|
Ф 1,89 |
|
0,47 |
0,03 |
2 |
3 |
|||||||||||
|
|
|
|
|
Ф |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
сумма |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,00 |
50 |
50 |
|
Сумма теоретических частот должна быть равна 50.
Между теоретическими и наблюдаемыми частотами есть расхождение, которое можно объяснить либо случайными причинами (например, недостаточным числом наблюдений), либо тем, что сделан неверный выбор закона распределения. Прове-
рим это с помощью критерия 2 Пирсона:
|
r |
(m mT )2 |
|||
расч2 |
|
i |
|
i |
. |
|
T |
|
|||
|
|
|
m |
|
|
|
i 1 |
|
i |
|
|
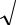
14
Результаты расчетов приведены в табл. 6.
Замечание. Для обеспечения большей обоснованности выводов интервалы с частотой объектов mi 5 следует объединить с соседними интервалами.
|
|
|
|
|
|
|
|
|
Таблица 6 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
№ |
mi |
|
miT |
|
mi miT |
|
(mi miT )2 |
|
(mi miT )2 |
|
|
||
|
mT |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
1 |
2 |
|
3 |
|
4 |
|
5 |
|
|
6 |
|
|
|
|
1 |
4 |
|
6 |
|
3 |
|
9 |
|
0,53 |
|
|
||
|
2 |
20 |
17 |
|
|
|
|
|
||||||
|
16 |
|
11 |
|
|
|
|
|
|
|
|
|
||
|
3 |
14 |
|
15 |
|
–1 |
|
1 |
|
0,07 |
|
|
||
|
4 |
8 |
|
11 |
|
–3 |
|
9 |
|
0,82 |
|
|
||
|
5 |
5 |
|
5 |
|
1 |
|
1 |
|
0,14 |
|
|
||
|
6 |
8 |
7 |
|
|
|
|
|
||||||
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
50 |
|
50 |
|
|
|
|
|
расч2 |
1,56 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
По прил. 5 žКритические точки распределения 2 ¤ из [1, 2] |
||||||||||||
определим |
предельно |
возможную |
величину |
расхождений |
||||||||||
крит2 |
( , k) в |
зависимости от заданного уровня значимости и |
||||||||||||
числа степеней свободы k. Здесь k r s 1, где r – число интервалов после объединения, s – число параметров распределения. В
нашем случае, 0,05, |
r 4, s 2, то |
есть k |
4 2 1 1. Так |
||
как крит2 |
(0,05; 1) 3,8 и |
расч2 |
1,56 3,8 |
крит2 , |
то различие меж- |
ду теоретическими и наблюдаемыми частотами незначимо. Вывод: производительность труда рабочих при проходке
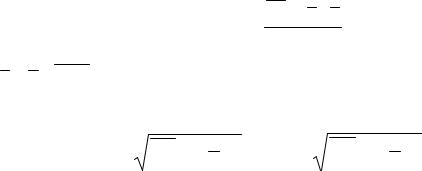
штрека распределена по нормальному закону с функцией плотно-
|
1 |
|
|
|
( x 0,22) 2 |
|||
|
|
|
|
2 |
|
|||
|
|
|
e 2 (0,053) |
|
||||
сти вероятности |
f ( x) |
|
|
|
. |
|||
0,053 |
|
|
||||||
|
||||||||
|
|
2 |
|
|
||||
15
Задача 2. Исследование линейной корреляционной зависимости между двумя случайными величинами.
Соответствующий теоретический материал, необходимый для выполнения задания, изложен в [1, гл. 18, с. 253 – 268].
Пример. Вычислить выборочный коэффициент корреляции между двумя случайными величинами X и Y, где Х – стаж работы работника, а Y – производительность его труда. Данные приведены в табл. 7. Найти коэффициент корреляции, составить уравнение линейной регрессии, построить линию регрессии, проверить значимость коэффициента корреляции.
Таблица 7
Х |
Y |
Х |
Y |
Х |
Y |
Х |
Y |
Х |
Y |
8 |
1,9 |
14 |
2,3 |
9 |
1,9 |
12 |
2,3 |
19 |
2,5 |
11 |
2,3 |
2 |
1,4 |
9 |
1,9 |
10 |
1,9 |
13 |
2,1 |
5 |
1,6 |
11 |
2,2 |
13 |
2,1 |
16 |
2,5 |
12 |
2,3 |
8 |
2,0 |
6 |
1,7 |
16 |
2,5 |
5 |
1,3 |
15 |
2,4 |
12 |
2,3 |
10 |
1,9 |
8 |
1,8 |
9 |
2,0 |
16 |
2,6 |
1 |
1,3 |
10 |
2,0 |
11 |
2,2 |
7 |
1,7 |
11 |
2,1 |
9 |
2,0 |
12 |
2,2 |
17 |
2,8 |
6 |
2,0 |
12 |
2,2 |
8 |
1,8 |
18 |
2,6 |
9 |
1,8 |
11 |
2,3 |
8 |
1,5 |
10 |
1,8 |
8 |
1,9 |
6 |
1,5 |
11 |
2,8 |
7 |
1,6 |
13 |
2,2 |
13 |
2,1 |
10 |
1,9 |
12 |
1,3 |
12 |
2,1 |
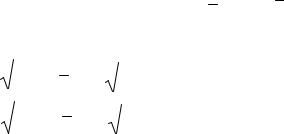
Решение. Выборочный коэффициент корреляции рассчитывается по формуле
rв xy x y , Sx Sy
где x , y , x y – средние значения для x, y, x y ;
Sx , S y – выборочные средние квадратические отклонения X и Y,
Sx |
x2 |
x |
2 , S y |
y2 |
y |
2 . |
Найдем составляющие для вычисления коэффициента корреляции, для чего заполним табл. 8.
16
Таблица 8
X |
Y |
X 2 |
XY |
Y 2 |
|
X |
|
Y |
|
X 2 |
|
XY |
|
Y 2 |
||||||||||
8 |
1,9 |
64 |
|
15,2 |
|
3,61 |
11 |
2,2 |
121 |
24,2 |
4,84 |
|||||||||||||
11 |
2,3 |
121 |
25,3 |
|
5,29 |
17 |
2,8 |
289 |
47,6 |
7,84 |
||||||||||||||
5 |
1,6 |
25 |
|
8 |
|
2,56 |
9 |
1,8 |
81 |
16,2 |
3,24 |
|||||||||||||
8 |
2 |
64 |
|
16 |
|
4 |
6 |
1,5 |
36 |
9 |
|
2,25 |
||||||||||||
12 |
2,3 |
144 |
27,6 |
|
5,29 |
10 |
1,9 |
100 |
19 |
3,61 |
||||||||||||||
1 |
1,3 |
1 |
|
1,3 |
|
1,69 |
12 |
2,3 |
144 |
27,6 |
5,29 |
|||||||||||||
9 |
2 |
81 |
|
18 |
|
4 |
10 |
1,9 |
100 |
19 |
3,61 |
|||||||||||||
8 |
1,8 |
64 |
|
14,4 |
|
3,24 |
16 |
2,5 |
256 |
40 |
6,25 |
|||||||||||||
10 |
1,8 |
100 |
18 |
|
3,24 |
5 |
1,3 |
25 |
6,5 |
1,69 |
||||||||||||||
13 |
2,2 |
169 |
28,6 |
|
4,84 |
9 |
2 |
81 |
18 |
4 |
||||||||||||||
14 |
2,3 |
196 |
32,2 |
|
5,29 |
7 |
1,7 |
49 |
11,9 |
2,89 |
||||||||||||||
2 |
1,4 |
4 |
|
2,8 |
|
1,96 |
6 |
2 |
36 |
12 |
4 |
|||||||||||||
11 |
2,2 |
121 |
24,2 |
|
4,84 |
11 |
2,3 |
121 |
25,3 |
5,29 |
||||||||||||||
6 |
1,7 |
36 |
|
10,2 |
|
2,89 |
11 |
2,8 |
121 |
30,8 |
7,84 |
|||||||||||||
10 |
1,9 |
100 |
19 |
|
3,61 |
12 |
1,3 |
144 |
15,6 |
1,69 |
||||||||||||||
10 |
2 |
100 |
20 |
|
4 |
19 |
2,5 |
361 |
47,5 |
6,25 |
||||||||||||||
12 |
2,2 |
144 |
26,4 |
|
4,84 |
13 |
2,1 |
169 |
27,3 |
4,41 |
||||||||||||||
18 |
2,6 |
324 |
46,8 |
|
6,76 |
12 |
2,3 |
144 |
27,6 |
5,29 |
||||||||||||||
8 |
1,9 |
64 |
|
15,2 |
|
3,61 |
15 |
2,4 |
225 |
36 |
5,76 |
|||||||||||||
13 |
2,1 |
169 |
27,3 |
|
4,41 |
16 |
2,6 |
256 |
41,6 |
6,76 |
||||||||||||||
9 |
1,9 |
81 |
|
17,1 |
|
3,61 |
11 |
2,1 |
121 |
23,1 |
4,41 |
|||||||||||||
9 |
1,9 |
81 |
|
17,1 |
|
3,61 |
12 |
2,2 |
144 |
26,4 |
4,84 |
|||||||||||||
13 |
2,1 |
169 |
27,3 |
|
4,41 |
8 |
1,5 |
64 |
12 |
2,25 |
||||||||||||||
16 |
2,5 |
256 |
40 |
|
6,25 |
7 |
1,6 |
49 |
11,2 |
2,56 |
||||||||||||||
8 |
1,8 |
64 |
|
14,4 |
|
3,24 |
12 |
2,1 |
144 |
25,2 |
4,41 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
y 2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
x y |
||||||||
|
|
|
|
|
|
|
|
|
|
10,42 |
2,03 |
122,46 |
22,26 |
4,25 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sx |
x2 |
x |
2 |
|
122,46 10,422 3,73; |
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
S y |
|
y2 |
|
y |
|
|
4,25 2,032 |
0,36. |
|||||
rв |
22,26 10,42 2,03 |
0,82 . |
|
||||||||||
|
|
|
|||||||||||
|
|
|
3,73 0,36 |
|
|
|
|
||||||
17
Уравнение линейной регрессии имеет вид:
y y rв Sy (x x) . Sx
В данном случае имеем: y 2,03 0,82 0,36 ( x 10,42) , 3,73
откуда y 0,08x 1,18.
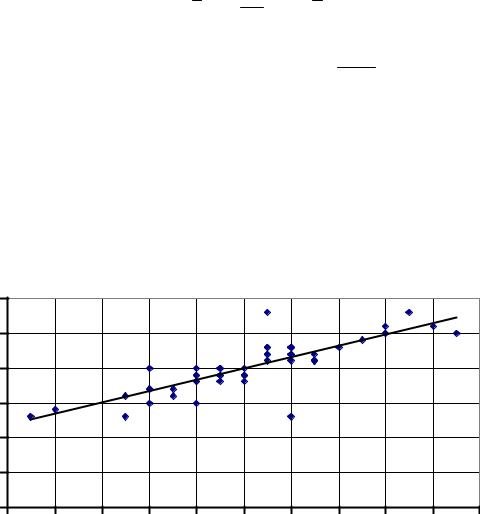
Построим на одном графике поле корреляции (имеющиеся точки), и полученную линию регрессии (рис. 3). Так как линия
регрессии – прямая, то |
ее строим |
по двум точкам: x1 2 , |
y1 0,08 2 1,18 1,34 ; x2 |
18, y2 |
0,08 18 1,18 2,62. |
Y |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2,5 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1,5 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 X |
|
Рис. 3. Поле корреляции и линия регрессии |
|
||||||||
Контрольная работа № 3
Задачи № 1 – 15. Теоремы сложения и умножения вероятностей. Формулы полной вероятности и Байеса.
1. Над изготовлением изделия работают последовательно трое рабочих. Качество изделия при передаче следующему рабочему не проверяется. Первый рабочий допускает брак с вероят-
18
ностью 0,1, второй – 0,2, третий – 0,05. Найти вероятность того, что при изготовлении изделия будет допущен брак.
2.В железнодорожном составе 50 вагонов с углем двух сортов. По сортности угля вагоны состава делятся на три группы:
25вагонов содержат 70% угля первого сорта и 30% угля второго сорта, 15 вагонов содержат соответственно 60% и 40%, остальные – 85% и 15%. Случайно взятый для анализа уголь оказался второго сорта. Какова вероятность, что он взят из вагона первой группы?
3.Прибор может работать в двух режимах: нормальном и аварийном. Нормальный режим наблюдается в 80% всех случаев работы прибора, аварийный – в 20% случаев. Вероятность выхода прибора из строя в нормальном режиме равна 0,1, в аварийном режиме– 0,7. Найти вероятность выхода прибора из строя.
4.Электрическая схема состоит из 3 блоков, работающих независимо друг от друга. Вероятности того, что они работают исправно, соответственно, равны 0,8; 0,4; 0,7. Схема годна к эксплуатации при наличии хотя бы двух исправных блоков из трех. Определить вероятность того, что схема будет работать.
5.В лотерее 20 билетов, из них 4 выигрышных и 16 пустых. Взят один билет, содержание которого осталось неизвестным. Какова вероятность того, что второй вынутый билет выигрышный?
6.В двух коробках находятся электролампы одинаковой величины и формы, но разной мощности. В первой коробке 4 лампы на 60 ватт и 6 на 100 ватт; во второй соответственно – 5 и
7.Из обеих коробок наудачу берут по одной лампе. Какова вероятность того, что обе лампы одинаковой мощности?
7.Система состоит из двух приборов: основного и дублирующего. Вероятность безотказной работы основного прибора системы равна 0,9, а дублирующего прибора – 0,8. При выходе основного прибора из строя происходит мгновенное переключение системы на дублирующий прибор. Определить вероятность безотказной работы системы.
8.Вероятности правильного определения химического состава детали для каждого из трех контролеров соответственно равны 4/5, 3/4 и 2/5. Найти вероятность того, что будет допущена
19
ошибка, если равновероятно деталь может попасть на проверку к любому из контролеров.
9.В трех одинаковых по виду и размеру коробках находятся по 20 сверл. В первой коробке 2 сверла бракованные, во второй – 3, в третьей – 5. Взятое наудачу сверло оказалось годным. Какова вероятность того, что оно взято из второй коробки?
10.Вероятность того, что изготовленная деталь окажется годной, равна 0,96. Контролер ОТК проверяет детали по упрощенной системе. Вероятность ошибки при проверке годных деталей равна 0,02, при проверке негодных деталей – 0,01. Какова вероятность того, что изделие, выдержавшее контроль, является годным?
11.У рабочего есть 10 сверл, 2 из которых имеют дефект. Вероятность того, что в течение смены сверло не придется менять, равна 0,8 для сверла, не имеющего дефект, и 0,2 – для сверла с дефектом. Наудачу взятое сверло в течение смены сломалось. Какова вероятность того, что было взято сверло без дефекта?
12.Болты изготавливаются на 3 станках, производящих соответственно 25%, 30%, 45% общего количества продукции. В продукции станков брак составляет соответственно 4%, 3%, 2%. Какова вероятность, что случайно взятый болт окажется дефектным?
13.Двадцати пяти студентам предоставлено для производственной практики 10 мест в Барнауле, 8 – в Хабаровске и 7 – в Томске. Найти вероятность того, что три друга попадут в один город.
14.Имеются две коробки с предохранителями. В первой коробке находится 12 штук, во второй – 10 штук, причем в каждой коробке есть по одному бракованному предохранителю. Изделие, взятое наудачу из первой коробки, перекладывается во вторую. Определить вероятность извлечения после этого бракованного предохранителя из второй коробки.
15.В телеателье поступили кинескопы с двух заводов: 35 штук с первого завода и 50 – со второго. Вероятность того, что кинескоп, изготовленный на первом заводе, не выйдет из строя в течение гарантированного срока, равна 0,85. Аналогичная вероятность для второго завода – 0,7. Наудачу выбранный кинескоп
