1. Примеры решения задач статики

Ниже приведены примеры составления уравнений равновесия (1.11) - (1.17). Порядок решения задач статики описан в третьей лекции. Там же приведены все основные случаи определения направлений реакций геометрических связей.

Пример 1. Определить реакции опор, если АС = CD = ВС = 2м, интенсивность распределенной нагрузки q = 5 кН/м, М =20 кН м, F =10 кН.

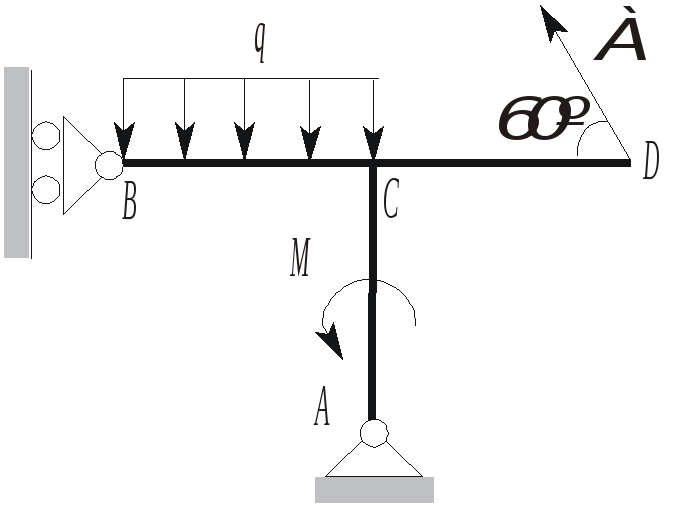
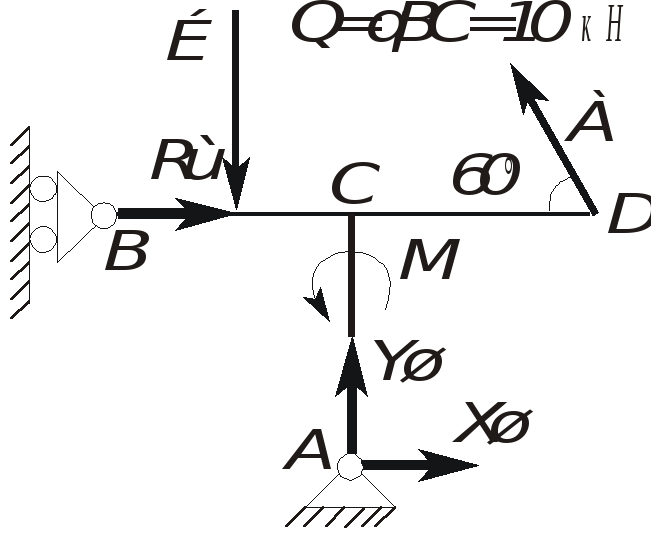
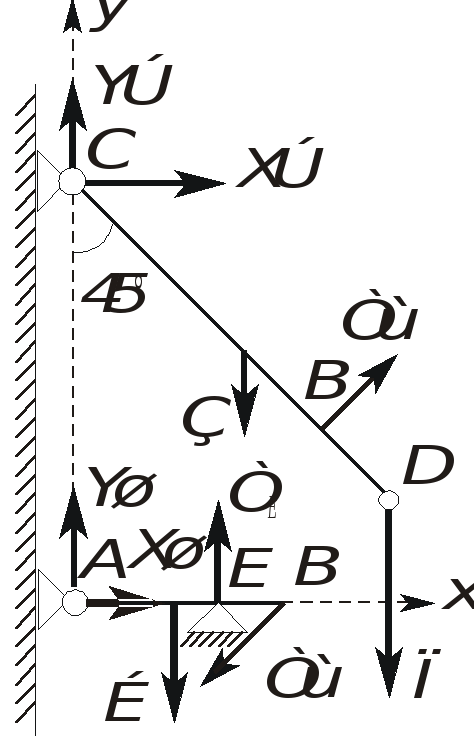
Решение. Заменив распределенную нагрузку сосредоточенной силой Q, а опоры - их

реакциями, составим уравнения равновесия для рамы, находящейся под действием произвольной плоской системы сил.

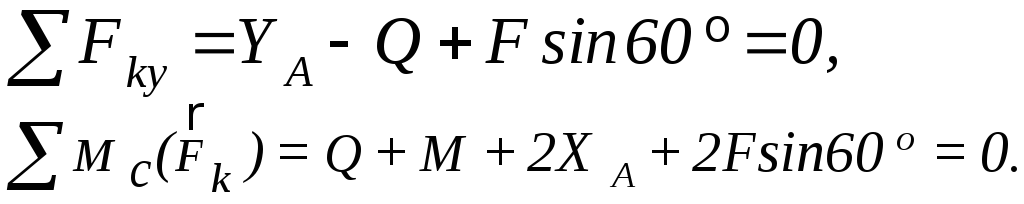
Xш=-0,5(Q+M)-Fsin60°=-23,7кН, Rщ= 0,5F-Xш=5кН, Yш= Q-Fsin 60°= -18,7кН .

Пример 2 . Балка АВ закреплена шарнирно в точке А и удерживается в горизонтальном положении тросами CD, DE и DF. Определить натяжение троса DE, если на балку действует сила Р=1100Н и пара сил с моментом m = 200 Нм.

Решение. Для балки АВ:

.

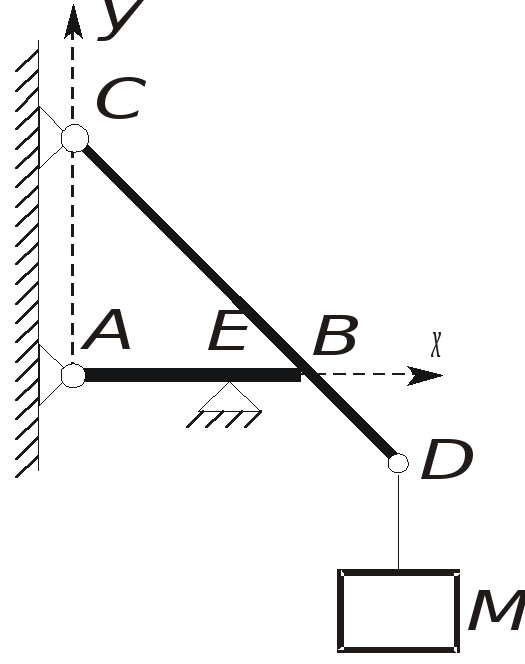
Для балки с тросом CD:

,

Пример 3 . Однородная горизонтальная балка АВ весом Р=3 кН опирается на гладкую опору Е и имеет шарнирное крепление в точке А, а однородная балка CD весом Q=6 кН с шарнирным креплением в точке В несет на конце D груз М весом G=1,2 кН. Определить реакции шарниров А, С и опоры Е, если СВ=3м, ВD=1м, ВЕ=K2 / 2м, ¦АСВ=45°.

Решение. Рассмотрим равновесие балок CD и АВ в отдельности. Уравнения равновесия для балки CD имеют вид:

Для балки АВ:

Решая совместно полученную систему шести уравнений равновесия, находим:

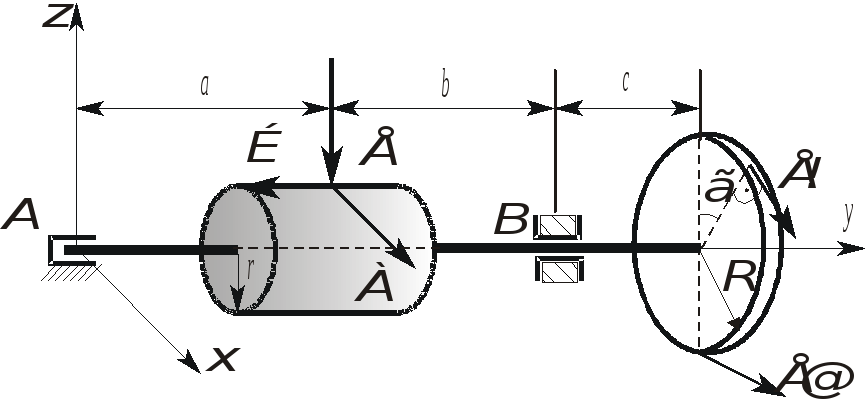
Пример 4: На валу червячной передачи жестко закреплен шкив ременной передачи. Определить силы натяжения Т₁ и Т₂ ветвей ремня и реакции подшипников А и В, если F=5 кН, T/F=1,25, Q/F=4, T₂/T₁=2, R=10см, r =2,5 см,  =30°, b/a=0,8, c/a=0,6 .

Решение.

Заменим связи (подшипники) их реакциями, составим уравнения равновесия:

Пример 4 . Однородная прямоугольная рама весом Р=200Н прикреплена к стене с помощью шарового шарнира А и петли В. Определить реакции опор и силу натяжения веревки, если а =30°.

Решение. Рассмотрим равновесие плиты, предварительно заменив связи их реакциями:

,

Лекция 8

Вопросы

1. Теорема Вариньона (общий случай)

2. Центр параллельных сил и центр тяжести

3. Способы определения положения центров тяжести

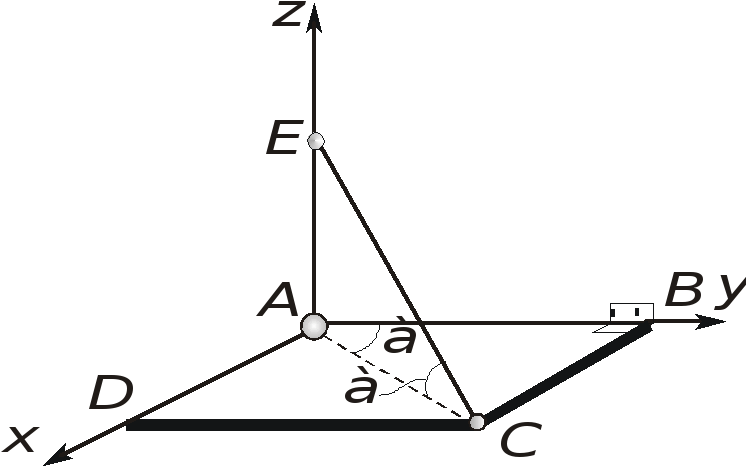
Покажем, что для любой системы сил, имеющей равнодействующую, справедлива следующая теорема Вариньона: момент равнодействующей относительно любого центра О равен сумме моментов всех сил системы относительно того же центра.

Доказательство.

Пусть на тело действует некоторая система сил (А!, А@, А#, . . . ,А%), имеющая равнодействующую К , линия действия которой проходит через некоторую точку С. Приложим в этой точке силу -К, равную равнодействующей, но направленную в противоположную сторону.

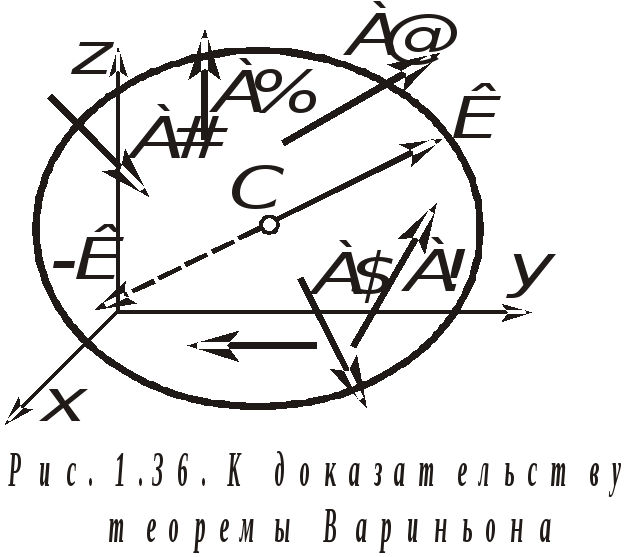
Тогда система сил (А!, А@, А#, . . . ,А%,-К) будет находиться в равновесии и для нее будет выполняться условие (1.10):

Ьн=0, т.е.

Учитывая, что получаемчто и требовалось доказать.

2. Центр параллельных сил и центр тяжести.

Вернемся к вопросу о сложении параллельных сил, рассмотренному в пятой лекции. Там было показано, что система двух параллельных и одинаково направленных сил А! и А@ имеют равнодействующую К=А!+А@, линия действия которой проходит через точку С, определяемую соотношением (1.5):

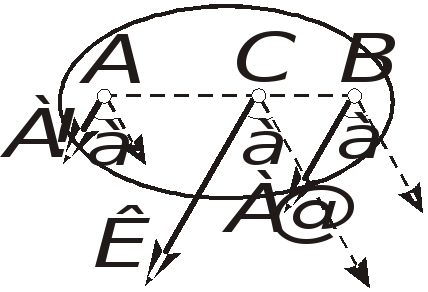
Очевидно, что если повернуть силы А! и А@ на один и тот же угол а в одну и ту же сторону, то на этот же угол повернется и их равнодействующая, причем ее линия действия будет проходить через ту же точку С , так как в определяющее положение точки С выражение (1.5) входят только модули сил F₁ и F₂ .

Рассмотрим теперь систему параллельных и одинаково направленных сил (А!, А@,А#,...,А%), приложенных в точках A₁(x₁,y₁,z₁), A₂(x₂,y₂,z₂),. . ., A_n(x_n,y_n,z_n) твердого тела (рис.1.34). Эта система сил имеет равнодействующую К=СА$, а ее линия действия проходит через точку С_n-1, положение которой найдем, определяя последовательно положения точек С₁, С_2,...,С_n-1 с помощью выражений

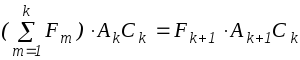, записанных для k=1,2,3, . , n -1 (1.18)

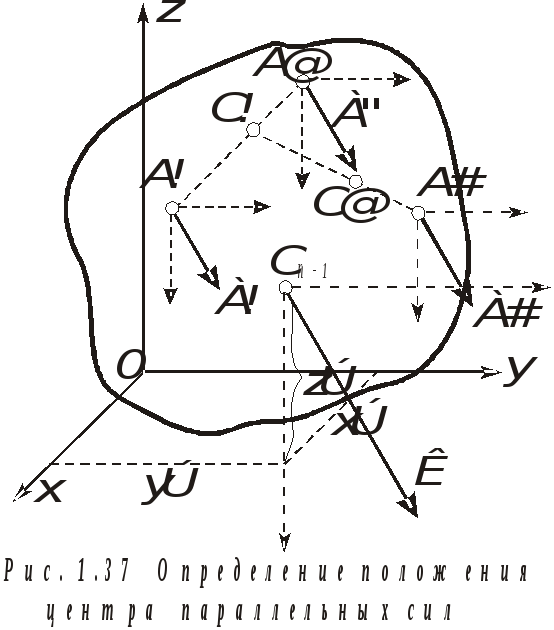
Так как в равенства (1.18) входят только модули рассматриваемых сил, положение точки С_n-1 относительно точек А₁, А₂, А₃, . . . , А_n не изменится при любых одинаковых изменениях ориентации сил системы.

Определение: точка, через которую проходит линия действия равнодействующей системы параллельных сил при любых поворотах этих сил на один и тот же угол в одну и ту же сторону, называется центром параллельных сил.

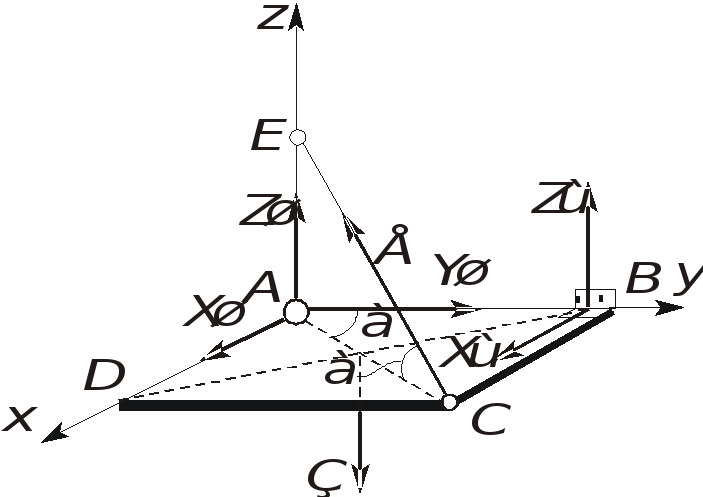
Найдем координаты этого центра в произвольной декартовой системе координат. Воспользуемся тем, что его положение не зависит от направления сил и направим все силы системы параллельно оси z (рис.1.34). Тогда по теореме Вариньона . Учитывая, что

, получаем .

Применяя теорему Вариньона относительно оси x и относительно оси z (в последнем случае направив все силы параллельно оси y) получаем аналогичные формулы для :

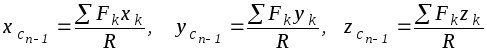. ( 1.19)

Полученные формулы используем для определения положения центров тяжести тел, находящихся в однородном гравитационном поле земного тяготения. Действительно, силы тяжести отдельных частиц тела, размеры которого малы по сравнению с радиусом Земли, образуют систему параллельных сил, аналогичную рассмотренной выше. Назовем равнодействующую сил тяжести отдельных частиц тела весом этого тела и будем обозначать его буквой З. Центром тяжести будем называть центр параллельных сил тяжести отдельных частиц тела и обозначать его буквойР. В новых обозначениях формулы (1.19) перепишутся в виде:

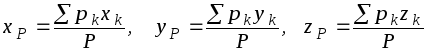(1.20)

Для однородных тел вес p_k отдельных частиц тела пропорционален объемам этих частиц : p_k= v_k, а вес тела пропорционален объему тела P= V ( - вес единицы объема). Подставляя данные выражения в (1.20), после сокращения на  , получаем формулы для определения центра тяжести объема:

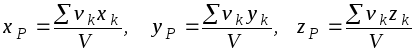(1.21)

Для однородных плоских пластин и изделий из однородных линейных элементов (например, из однородной проволоки постоянного сечения), вводя вес единицы площади и вес единицы длины, аналогичных образом получаем формулы для определения центра тяжести площади и центра тяжести линии:

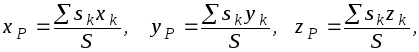(1.22)

где S - площадь всей пластины, s_k - площади ее частей.

(1.23)

где L - длина всей линии, l_k - длина ее частей.

3. Способы определения положения центров тяжести.

а) Способ симметрии. Если однородное тело имеет плоскость симметрии, ось симметрии или центр симметрии, то его центр тяжести находится соответственно или в плоскости симметрии, или на оси симметрии, или в центре симметрии.

б) Способ разбиения. Если тело можно разбить на конечное число частей, для которых положения центров тяжести известны, то координаты центра тяжести всего тела можно непосредственно вычислить по формулам (1.21) - (1.23).

Пример 1. Найти координаты центра тяжести тела, имеющего вид стула, состоящего из стержней одинаковой длины и веса. Длина стержня равна l = 44 см.

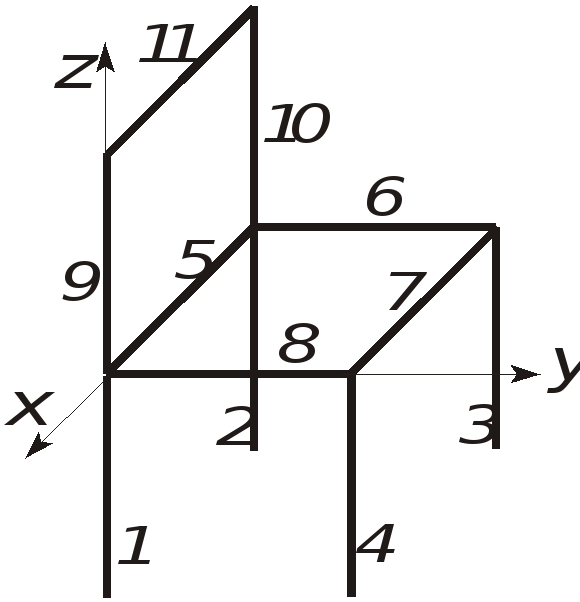
Решение. Так как тело имеет плоскость симметрии и центр тяжести лежит в этой плоскости, то x_c=-22 см. Остальные координаты определяем по формулам (1.23).

y_c=[(l₃+l₄+l₇)44+(l₆+l₈)]/(11·44)=16см.

z_c=[-22(l₁+l₂+l₃+l₄)+l₁₁44+(l₉+l₁₀)]/(11·44)=0.

в) Интегрирование. Если тело не удается разбить на несколько частей, положение центров тяжести которых известны, то тело разбивают на произвольные малые объемы v_k и формулы (1.21) принимают вид:

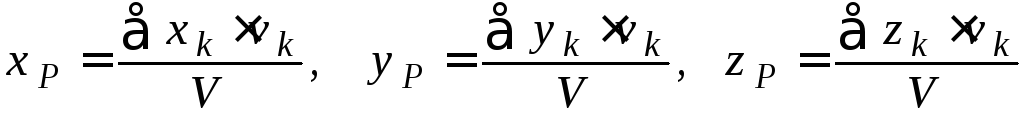, (1.24)

где x_k, y_k, z_k - координаты некоторой точки, расположенной внутри объема v_k

Переходя в формулах (1.24) к пределу при v_k  0, получаем:

(1.25)

Аналогичным образом, переходя в формулах (1.22) и (1.23) к пределу, получаем интегральные выражения для определения координат центров тяжести площадей и линий:

(1.26)

(1.27)

Пример 2. Найдем положение центра тяжести дуги окружности АВ радиуса R c центральным углом 2а. В силу симметрии центр тяжести лежит на оси x. Для определения координаты y выделим на дуге элемент длиной dl = Rdф, положение которого определяется углом ф. Координата x этого элемента равна x = = Rcosф, длина АВ=L=R2а. тогда согласно (1.27):

.

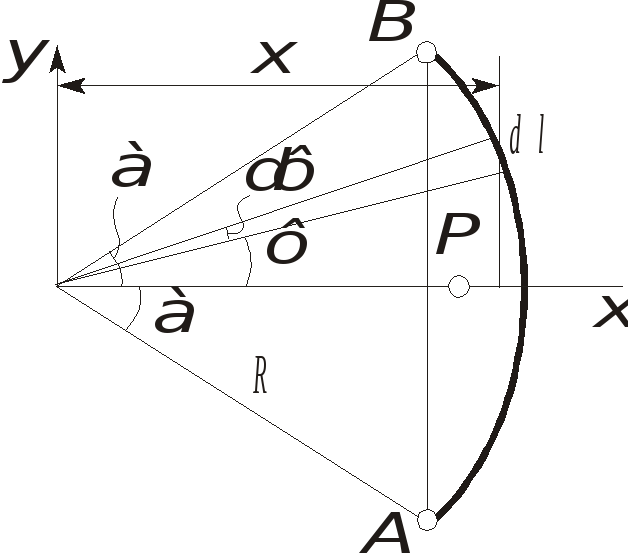
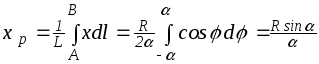г) Способ дополнения (способ отрицательных масс). Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющим вырезы. При этом центры тяжести тел без вырезов и центры тяжести самих вырезов должны быть известны.

Пример 3. Дана однородная квадратная пластина ABDE со стороной а. Найти внутри квадрата такую точку С, чтобы она была центром тяжести площади, которая получится, если из квадрата вырезать равнобедренный треугольник ACB.

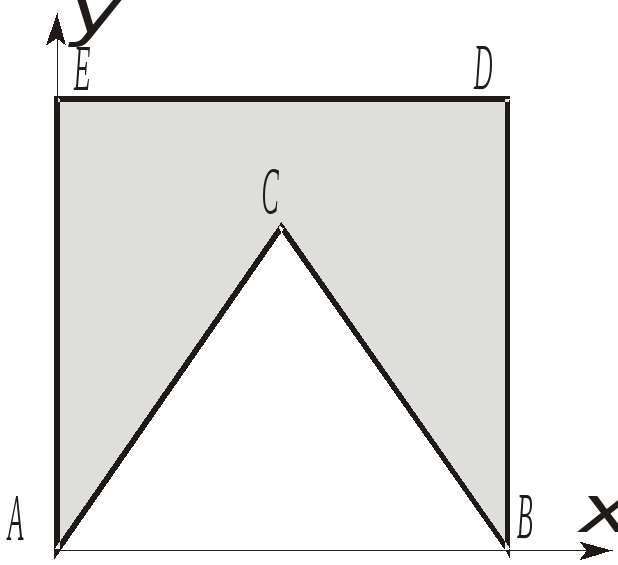
Решение: В силу симметрии x_c=a/2. Для определения у_с используем метод дополнения. Пусть S - площадь квадрата с вырезом, S₁ , y₁ - площадь квадрата без выреза и координата y его центра тяжести, S₂ , y₂ - площадь и координата y центра тяжести треугольника АСВ. Согласно (1.22): y_c= S_ky_k / S=(S₁y₁ - S₂y₂)/ S = (a² a/2-0,5ay_c y_c/3)/(a²- 0,5ay_c), 2y_c² - 6y_c+3=0 , откуда у_с= 0,61а (второй корень y_c=2,4a не подходит по смыслу).

Лекция 9

Вопросы