1. Понятие алгебраического момента силы.

2. Момент силы относительно точки.

3. Теорема Вариньона для системы сходящихся сил.

4. Момент силы относительно оси.

1. То, что понятия силы явно недостаточно для решения многих задач механики, знали еще в Древней Греции. Новый элемент - произведение силы на ее расстояние до точки опоры, приводящий тело во вращение, был введен Архимедом при изложении им теории равновесия рычага. В современной трактовке, введенный Архимедом новый силовой фактор, называется алгебраическим моментом. К необходимости введения этого понятия мы приходим при попытке ответить, например, на следующий вопрос: при каком соотношении длин L₁ , L₂ и весов P₁ , P₂ невесомый стержень (рис. 1.21) будет находиться в равновесии в горизонтальном положении?

Рис. 1.21. К определению алгебраического момента

Ответ на этот вопрос следующий: стержень будет в равновесии, если:

P₁ L₁ = P₂ L₂

или

P₁ L₁ - P₂ L₂ = 0.

Другими словами, при равновесии рычага должны быть равны произведения сил, расположенных справа и слева от точки опоры О, на кратчайшие расстояния от точки О до линий действия этих сил.

Если отвлечься от рассмотренной выше задаче о равновесии рычага, то алгебраический момент силы относительно произвольного центра О можно определить как взятое со знаком плюс или минус произведение модуля силы на плечо. При этом плечом называют кратчайшее расстояние от центра О до линии действия силы (рис. 1.22)

Рис. 1.22. К определению алгебраического момента

Правило знаков: если сила стремится повернуть тело, к которому она приложена, против часовой стрелки, то момент считается положительным, если по часовой - отрицательным. Понятия алгебраического момента вполне достаточно для описания действия на тело плоских систем сил. Для описания действия пространственной системы сил вводится понятие вектора-момента относительно точки и понятие осевого момента.

2. Момент силы относительно точки

Моментом силы относительно точкиО называется вектор , равный векторному произведению , где - радиус-вектор, определяющий положение точки приложения силы относительно точкиO.

Рис. 1.23. К определению момента силы относительно точки

По определению векторного произведения вектор приложен в точкеO и направлен перпендикулярно плоскости, содержащей перемножаемые векторы ( плоскость треугольника OАВ) в ту сторону, откуда поворот от вектора к вектору виден происходящим против хода часовой стрелки (рис.1.23). Модуль вектора-момента равен:

,

где h - плечо силы относительно точкиO.

Введенный таким образом момент, полностью определяет вращательный эффект приложенной к телу силы: его линия действия определяет плоскость вращения, его направление - направление вращения, его модуль - интенсивность вращательного воздействия силы на тело.

3. Теорема Вариньона для системы сходящихся сил

Момент равнодействующей, относительно некоторой точки О, равен сумме моментов составляющих сил относительно той же точки.

Данная теорема справедлива для любой системы сил, имеющей равнодействующую. Приведем здесь ее доказательство для системы сходящихся сил.

Пусть является равнодействующей системы сходящихся сил , т.е.

.

Тогда по определению момента

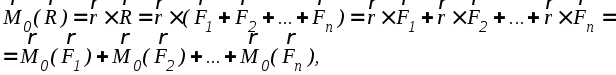
что и требовалось доказать.

4. Момент силы относительно оси

Моментом силы относительно оси называется проекция на эту ось вектора момента данной силы относительно любой точки, лежащей на этой оси.

Пусть необходимо вычислить момент силы относительно осиZ. Выберем на этой оси (рис. 1.24) произвольную точку O и проведем через нее оси X и Y. По определению момент силы относительно точкиO равен векторному произведению :

Рис. 1.24. Определение осевых моментов

Из векторной алгебры известно, что выражения, стоящие в скобках при единичных ортах представляют собой проекции векторного произведения на оси x, y, z соответственно:

,

, (1.3)

.

Анализируя последнее из выражений (1.3) можно заметить, что оно не содержит координаты z. Это значит, что значение осевого момента M_z не зависит от выбора точки О на оси z. Отсутствие в данном выражении R_z говорит о том, что осевой момент создают лишь перпендикулярные данной оси составляющие силы. Это означает, что если сила параллельна какой-либо оси, то ее момент относительно этой оси равен нулю. Кроме того, отсюда же (и из теоремы Вариньона) следует простое правило вычисления осевых моментов:

Момент силы ™ относительно какой-либо оси равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси, взятому относительно точки пересечения оси с плоскостью.

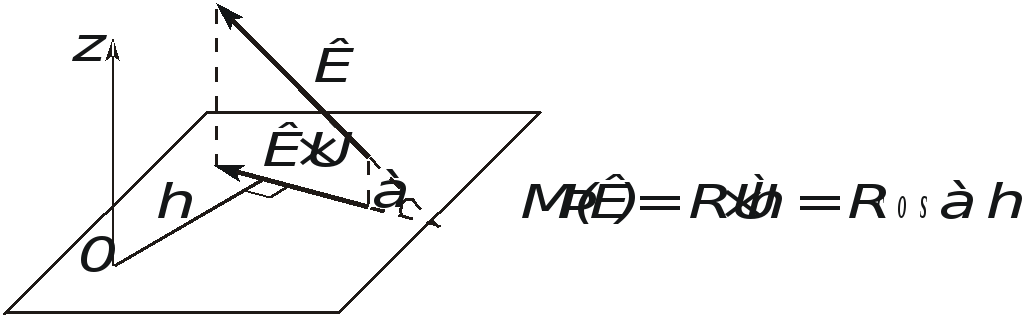
Рис. 1.25. Вычисление осевого момента

Момент будет иметь знак плюс, когда с положительного конца оси поворот, который стремится совершить сила , виден происходящим против хода часовой стрелки. Из рис. 1.25 видно, что если линия действия силы , а, следовательно и силы , пересекает ось Z, то ее осевой момент будет равен нулю ( т.к. в этом случае h = 0 ).

Лекция 5

Вопросы

1. Сложение параллельных сил.

2. Пара сил и ее момент.

3. Теорема о параллельном переносе силы.

1. Рассмотрим вопрос о сложении двух параллельных и направленных в одну сторону сил (рис. 1.26)

Рис. 1.26. Сложение двух параллельных сил, направленных в одну сторону

Пусть на твердое тело в точках А и В действуют параллельные силы и(рис. 1.26). Приложим в этих точках уравновешенную систему двух равных по величине силии направленных вдольАВ в противоположные стороны. Заменим системы сил ,и,их равнодействующимии. Затем перенесемивдоль их линий действий в точкуD и заменим их одной силой К, являющейся равнодействующей сил А! и А@:

.

Найдем линию действия силы . Из подобия треугольниковACD и BMN следует

, .

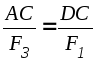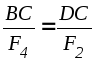Учитывая, что F₃ = F₄ , получаем

или . (1.5)

Таким образом, система двух параллельных и одинаково направленных сил имеет равнодействующую, равную сумме этих сил и направленную в ту же сторону.

Согласно (1.5), линия действия равнодействующей делит отрезок АВ на части, обратно пропорциональные величинам сил и.

Аналогичным образом рассматривается случай сложения двух параллельных не равных по величине и противоположно направленных сил. Ниже приводятся без доказательства лишь результаты такого сложения.

Рис. 1.27. Сложение двух параллельных и противоположно направленных сил

Изображенная на рис 1.27 система сил имеет равнодействующую , которая равна разности сили направлена в сторону большей по величине силы. Ее линия действия делит отрезокАВ на части обратно пропорциональные силам F₁ и F₂ внешним образом (точка С лежит за большей по величине силой F₂ ): ,. (1.6)

Еще раз обращаем внимание на то, что в рассматриваемом случае

2. Пара сил и ее момент

Займемся не рассмотренным в предыдущем пункте случаем, когда складываются две равные, параллельные, не лежащие на одной прямой и противоположно направленные.

Если использовать формулу (1.6) для вычисления равнодействующей такой системы сил, то мы получим , что казалось бы, должно означать уравновешенность данной системы сил. Вместе с тем, очевидно, что под действием такой системы сил тело начнет вращаться. Остается признать, что такая система является исключением среди систем двух параллельных сил и не имеет равнодействующей. Именно поэтому ее рассматривают как самостоятельный силовой фактор и называют парой сил.

Так как вращательный эффект сил характеризуется их моментом, вычислим момент пары сил относительно произвольного центра О, как сумму моментов отдельных сил пары (рис. 1.28)

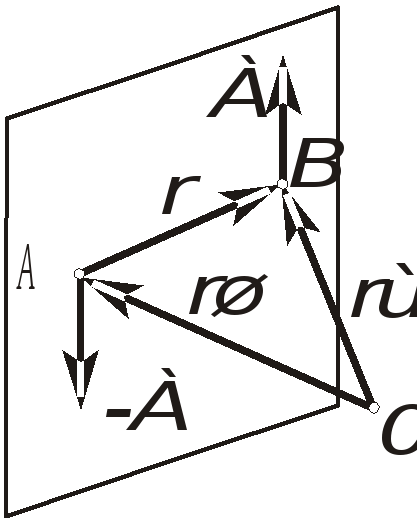
Рис. 1.28. К определению момента пары сил

(1.7)

Данный результат означает, что момент пары сил не зависит от выбора точки О и равен моменту одной из сил пары относительно точки приложения другой силы, т.е.

. (1.8)

Модуль момента пары сил равен m = F r sin = F h, где h - расстояние между линиями действия сил пары, называемое плечом пары. Вектор направлен перпендикулярно плоскости действия пары в ту сторону, откуда вращение видно против хода часовой стрелки.

Из принятого определения момента пары, как суммы моментов отдельных сил пары относительно произвольного центра (1.7) и независимости момента пары сил от выбора центра О (1.8), следует:

a) две пары сил, имеющие одинаковые моменты, эквивалентны (т.е. оказывают на тело одинаковое механическое действие). Это означает, что две пары сил, независимо от их расположения в данной ( или в параллельной) плоскости, независимо от того, чему равны в отдельности модули их сил и плечи, будут эквивалентны, если будут равны их моменты;

б) момент пары является свободным вектором (т.е. его можно считать приложенным в любой точке тела).

Примеры эквивалентных по действию на тело пар сил (рис. 1.29):

Рис. 1.29. Примеры эквивалентных по действию пар сил

в) если на тело действуют несколько пар сил, то сумма моментов всех сил, образующих эти пары, относительно любого центра будет равна геометрической сумме моментов отдельных пар сил и, следовательно, вся совокупность этих пар будет эквивалентна одной паре с моментом , (1.9)

где - моменты отдельных пар сил.

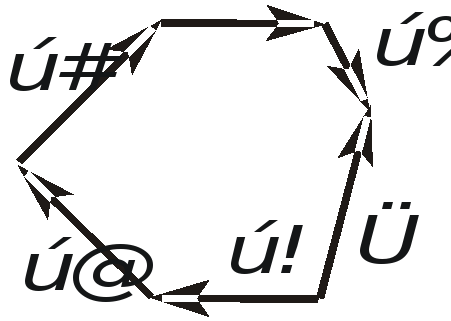
Рис. 1.22. Векторный многоугольник моментов пар сил

3. Теорема о параллельном переносе силы

Силу, приложенную к абсолютно твердому телу, можно, не изменяя оказываемого ею действия, параллельно перенести в любую другую точку тела, добавив при этом пару сил с моментом, равным моменту переносимой силы относительно ее новой точки приложения. Докажем эту теорему.

Пусть в точке А приложена сила, которую мы хотим перенести в точку В. Приложим в точке В уравновешенную систему двух сил, равных по величине переносимой силе, как показано на рисунке. Заменив образовавшуюся при этом пару сил (которую называют присоединенной) ее моментом и перенеся данный момент, как свободный вектор, в точку В, получаем формулируемое в теореме утверждение.

Рис. 1.24. Эквивалентные преобразование при параллельном переносе силы

Пример 1.

На барабан 1 радиуса r намотаны в противоположных направлениях две нити, к концам которых прикладывают силы и . На барабан 2 того же радиуса намотана одна нить, к которой прикладывают силу (рис. 1.29). Рассмотрим, чем будут отличаться действия этих сил.

Рис. 1.29. Примеры действия пар сил

На барабан 1 действует только пара сил с моментом, численно равным2rF, вращающим барабан. Силу, действующую на барабан 2, можно заменить силой , приложенной к оси барабана, и парой силс моментом2rF . Итак, оба барабана будут вращаться одинаково. Но при этом ось второго барабана будет испытывать давление, равное 2F, а ось первого барабана никакого давления не испытывает.

Лекция 6

Вопросы