
MT2012em домашняя работа
.pdf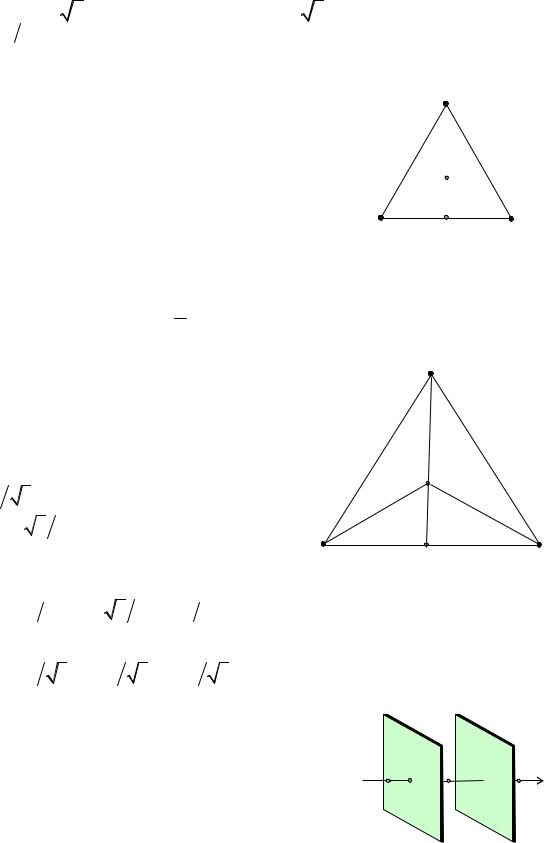
|
q |
|
|
|
|
9 Н м |
2 |
|
10−9 Кл |
|
|
|
Н |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
E = k |
|
|
|
5 = 9 10 |
|
|
|
|
|
|
|
|
|
|
|
5 = 8050 |
|
|
(2.5) |
|
|||
(c 2 ) |
2 |
|
|
Кл |
2 |
|
0, 05 |
2 |
м |
2 |
Кл |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: Е = 8050 В/м. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Задача 3. В вершинах равностороннего треугольни- |
|
q2 |
|
|
|||||||||||||||||||
ка помещены заряды q1 = q3 = 1,5 нКл, q2 = –2 нКл. Сто- |
|
|
|
|
|||||||||||||||||||
рона треугольника |
|
равна a = 0,2 |
м. Определить |
раз- |
a |
C |
a |
|
|||||||||||||||
ность потенциалов между точками поля В и С, распо- |
|
|
|
||||||||||||||||||||
ложенными в центре и на середине одной из сторон q |
|
|
q |
3 |
|||||||||||||||||||
треугольника. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
B |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a
Решение. Потенциал электрического поля точечного
заряда q на расстоянии r от него может быть определён по формуле:
ϕ = k q |
|
r . |
(3.1) |
Согласно принципу суперпозиции, потенциал |
A q2 |
электрического поля в заданной точке поля равен |
|
сумме потенциалов полей от всех зарядов: |
|
ϕ = ϕ1 + ϕ2 + ϕ3 . |
|
|
|
|
|
|
|
|
|
|
|
(3.2) |
|
|||||||||||||||
Расстояния от всех зарядов до точки С одина- |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ковое: АС = a 3 , а расстояние от заряда q2 до |
|
|||||||||||||||||||||||||||
точки B: АB = a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q1 |
|||
|
|
3 2 . Тогда потенциалы в точ- |
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
ках В и С равны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ϕ |
|
= k |
|
q1 |
|
+ k |
|
q2 |
|
+ k |
|
|
q3 |
|
= 166 В, |
|
||||||||||||
B |
a 2 |
|
|
|
|
|
|
a 2 |
|
|||||||||||||||||||
a |
3 2 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ϕC = k |
|
|
q1 |
|
|
|
+ k |
|
q2 |
|
|
|
+ k |
|
q3 |
|
|
|
= 78 В. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
a |
3 |
a |
3 |
a |
3 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Ответ: ϕ = ϕB − ϕC = 166 − 78 = 88 В.
Задача 4. Электрическое поле создано двумя параллельными заряженными пластинами в форме квадрата. Заряды q1 = –30 нКл и q2 = 10 нКл равномерно распределены по поверхностям пластин. Длина стороны каждой пластины a = 20 см. Расстояние между ними d = 2 мм.
C
q3
a/2 B a/2
|
|
(3.3) |
|
|
(3.4) |
q1 |
|
q2 |
A |
B |
C |
|
|
|
O |
|
x |
1)Рассчитать напряжённость электрического поля в точках A, B, C, находящихся на расстоянии h = 1 мм от пластин.
2)Найти силу взаимодействия плоскостей.
10

Решение. 1) Равномерно заряженная пластина создаёт вокруг себя однородное электрическое поле вдали от границ напряжённостью E , направленной перпендикулярно её поверхности:
σ |
|
|
E = |
, |
(4.1) |
2ε0 |
где σ – поверхностная плотность заряда, т.е. заряд на единицу площади пластины,
ε0 – электрическая постоянная ( ε0 = 8, 85 10−12 Ф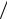 м ). Если заряд пластины положительный, то напряжённость электрического поля направлена от пластины в бесконечность, а если заряд отрицательный, то – из бесконечности к пластине.
м ). Если заряд пластины положительный, то напряжённость электрического поля направлена от пластины в бесконечность, а если заряд отрицательный, то – из бесконечности к пластине.
В условиях данной задачи, точки, в которых надо определить напряжённость, находятся далеко от границ: расстояние от точек А, В и С до пластин 1 мм, а расстояние до границ более 10 см. Поэтому можно воспользоваться формулой (4.1). Поверхностные плотности зарядов пластин могут быть рассчитаны следующим образом:
σ1 |
= |
q1 |
= |
−30 10−9 |
Кл |
= −7, 5 10 |
−7 Кл |
, |
σ2 |
= |
q2 |
= 2, 5 |
10 |
−7 |
Кл |
. |
(4.2) |
||
a2 |
0,22 м2 |
|
м2 |
a |
2 |
|
м2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Тогда, напряжённости полей от каждой пластины равны:
E = |
|
σ1 |
|
= |
|
7, 5 10−7 |
Кл м2 |
= 4, 24 10 |
4 |
|
В |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
2ε |
|
|
|
|
|
2 8,85 10-12 Ф м |
|
|
|
|
м |
||||||
|
0 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
E = |
|
σ2 |
|
= |
|
2, 5 10−7 |
Кл м2 |
= 1, 41 10 |
4 |
|
В |
|||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
2ε |
|
|
|
|
|
2 8,85 10-12 Ф м |
|
|
|
|
м |
|||||
|
|
0 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
По принципу суперпозиции напряжённости полей надо складывать согласно правилам векторного сложения:
E = E1 + E2 . |
(4.5) |
Из рис. видно, что
|
σ1 |
|
|
|
|
|
|
A |
|
|
|
EА |
|
E |
|
|
|
|
В |
|
|
|
|
EА2 |
EА1 |
|
|
|
EВ1 |
||
|
|
|
|
|
|
|
|
–
EA = EA1 − EA2 = (4, 24 −1, 41) 104 = 2, 83 104 В м, EВ = EВ1 + EВ2 = (4, 24 + 1, 41) 104 = 5, 65 104 В
м, EВ = EВ1 + EВ2 = (4, 24 + 1, 41) 104 = 5, 65 104 В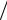 м, EС = EA = 2, 83 104 В
м, EС = EA = 2, 83 104 В м.
м.
(4.3)
(4.4)
|
σ2 |
|
||
B |
|
|
E |
C |
|
|
|||
|
|
|
С |
|
|
|
|
|
|
|
|
EС1 |
E |
|
EВ2 |
|
|
||
|
|
|
С2 |
|
|
|
|
|
|
+
(4.6)
(4.7)
(4.8)
11
2) Пластины имеют заряды противоположных знаков, поэтому они будут притягиваться друг к другу. Для определения силы взаимодействия между заряженными пластинами воспользуемся формулой:
F1 = |
q1 |
E2 |
или F2 = |
q2 |
E1 . |
(4.9) |
В соответствии с III законом Ньютона, силы F1 и F2 равны по модулю и противо- |
||||||
положны по направлению. |
|
|
|
|
||
F1 = F2 = 30 10−9 1, 41 104 |
= 10 10−9 4, 24 104 = 4, 24 10−4 Н . |
(4.10) |
||||
Ответ: 1) EС = EA = 28, 3 кВ м; EВ = 56, 5 кВ
м; EВ = 56, 5 кВ м;
м;
2) F = 0, 424 мН
Задача 5. Полубесконечная нить имеет линейную
плотность заряда τ = 100 нКл/м. Определить силу, |
τ |
q0 |
A |
|
|||
действующую со стороны поля нити на точечный |
|
|
|
|
a |
|
|
заряд q0 = 3 нКл, находящийся в точке А, удаленной |
|
|
|
|
|
|
|
|
|
|
|
от конца нити на расстояние, равное а = 0,2 м. |
|
|
|
Решение. Если известна напряжённость электрического поля нити в точке А, то найдём силу, действующую на заряд q0, по формуле:
F = |
q0 |
EA . |
(5.1) |
Чтобы найти напряжённость EA , надо разбить весь заряд нити на точечные бесконечно малые заряды dq, определить напряжённость электрического поля dE от каждого точечного заряда и воспользоваться принципом суперпозиции.
Напряжённость поля dE от точечного заряда dq определяется по формуле:
|
|
||
dE = k |
dq |
er . |
(5.2) |
2 |
|||
|
r |
|
|
|
|
|
|
|
dq = τdx |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
A dE |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
a |
|
X |
|
|
|
|
|
|
dx |
|
O |
|
|
||||||||
Расстояние от заряда до точки А: |
r = a − x . Тогда, с учётом того, что напряжён- |
||||
ности полей направлены вдоль оси OX: |
|
||||
dEx = k |
τdx |
|
. |
(5.3) |
|
|
|
|
|||
(a − x ) |
2 |
||||
|
|
|
|
||
12

По принципу суперпозиции:
0 |
τdx |
|
|
1 |
|
|
0 |
|
k τ |
|
9 10 |
9 |
10 |
−7 |
В |
|
|
|
|
|
|
|
|
||||||||||||
EA = ∫dEx = ∫ k |
|
= k τ |
|
|
|
= |
= |
|
|
= 4500 |
. (5.4) |
||||||
(a − x ) |
2 |
a − x |
|
|
|
|
|
|
|
м |
|||||||
−∞ |
|
|
|
−∞ |
|
a |
0, 2 |
|
|
|
|||||||
|
|
|
|
|
|
||||||||||||
Ответ: F = q0 EA = 3 10−9 4500 = 1, 35 10−5 Н.
Задачи для самостоятельного решения
Эти задачи необходимо представить на проверку к следующему практиче- скому занятию на отдельном листе. Условия задач не переписывать.
1.1. С какой силой взаимодействовали бы два медных шарика массой m = 1 г каждый, находясь на расстоянии R = 1 м друг от друга, если суммарный заряд всех электронов в них отличался бы на 1% от суммарного заряда всех ядер? См. значения физических величин на стр. 53.
1.2. В вершинах квадрата со стороной а = 0,1 м по-
мещены заряды q1 = q2 = –20 нКл, q3 = q4 = +20 нКл.
Определить напряжённость E и потенциал ϕ электрического поля в точках: 1) A (в центре квадрата);
2)B (на середине стороны);
3)C (на середине стороны).
+q |
a |
+q |
a |
A |
B |
–q 

 –q
–q
C
1.3.Две круглые параллельные пластины радиусом R = 0,4 м равномерно заряжены по всей поверхности зарядами q1 = –20 нКл и q2 = +20 нКл. Расстояние между ними d = 1 мм. Оси пластин совпадают.
1)Рассчитать напряжённость электрического поля в пространстве между ни-
ми.
2)Найти силу взаимодействия плоскостей.
1.4.Сила притяжения F между пластинами плоского воздушного конденсато-
ра равна 50 мН. Площадь S каждой пластины равна 200 см2. Найти напряжён-
ность электрического поля E конденсатора. |
|
|
|
|
|
1.5. Тонкий прямой стержень длиной l=0,1 м несёт |
|
q |
|
A |
|
равномерно распределенный заряд q = 30 нКл. Опре- |
|
l |
|
l |
|
|
|
|
|||
делить напряжённость поля, создаваемого этим заря- |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
дом в точке А, расположенной на продолжении оси стержня и удалённой от его ближнего конца на расстояние, равное длине стержня.
13
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2. ТЕОРЕМА ГАУССА ДЛЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
Основные понятия: поток вектора напряжённости электрического поля, замкнутая поверхность, теорема Гаусса.
Контрольные вопросы
1.Что такое поток векторного поля через поверхность?
2.Сформулировать теорему Гаусса для электрического поля.
3.В каких единицах в системе СИ измеряется поток вектора напряжённости электрического поля?
4.Какой знак будет иметь поток электрического поля, если напряжённость направлена внутрь замкнутой поверхности?
5.При каких условиях поток вектора E через замкнутую поверхность равен нулю?
Примеры решения задач
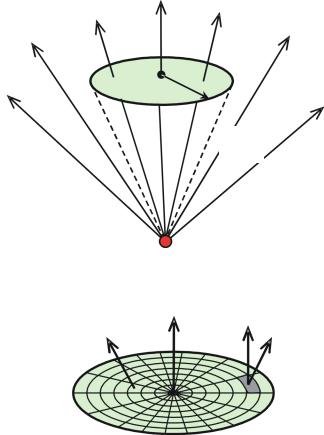
Задача 1. Электростатическое поле создано точечным зарядом q = 1 нКл. Определить поток вектора напряжённости через круглую площадку радиусом R = 1 см. Заряд равноудалён от краёв площадки на расстояние 2R.
Решение. Определить поток вектора напряжённости электрического поля через круглую площадку S (рис. 1.1) можно, например, путём интегрирования:
ΦE = ∫∫EidS . |
(1.1) |
S |
|
Для этого необходимо разбить площадку на бесконечно малые элементы. Один из способов такого разбиения показан на рис. 1.2. Для того чтобы найти интеграл (1.1), необходимо проинтегрировать элементарные потоки через каждую бесконечно малую площадку dS. Это сделать довольно сложно,
поскольку напряжённость E различная
в каждом элементе поверхности dS и по направлению и по модулю.
Существует другой способ определения потока вектора напряжённости
S R
2R
|
q |
|
|
|
Рис. 1.1 |
|
|
|
|
|
|
E |
dS |
|
|
E |
|
||
|
|
E |
|
|
|
|
|
|
|
|
S |
|
Рис. 1.2 |
|
|
14
через поверхность с использованием теоремы Гаусса: поток вектора напряжённости электрического поля через замкнутую поверхность равен сумме зарядов, заключённых внутри неё, делённой на электрическую постоянную ε0,
ΦE 0 = ∫∫ |
|
∑qi |
|
|
||
i |
. |
(1.2) |
||||
EidS = |
||||||
|
|
|
|
|
||
S |
0 |
|
ε0 |
|
|
|
|
|
|
|
|
||
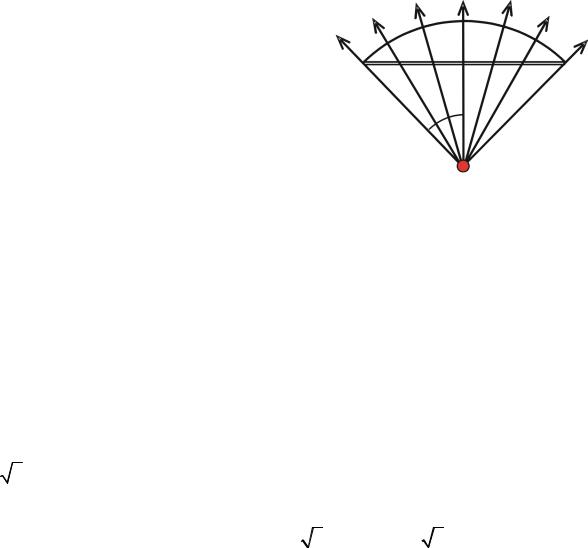
Чтобы применить теорему Гаусса, необходимо дополнить круг S, например, частью сферической поверхности Sсф радиусом 2R, чтобы получить замкнутую поверхность S0 (рис. 1.3). Заряд q находится снаружи поверхности S0, а внутри неё зарядов нет, поэтому сумма в формуле (1.2) равна нулю. Поток ΦE0 складывается из потока через круг ΦE и потока через сферическую поверхность ΦE сф :
Φ E 0 = Φ E + Φ E сф |
= 0 . |
(1.3) |
|
|
|
|
||
Следовательно, |
|
|
|
|
|
|
|
R |
ΦE = −ΦE сф = − ∫∫ |
|
|
|
|
|
|
S0 |
|
EidS . |
(1.4) |
|
|
|
||||
S сф |
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
2R |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Найти поток вектора E |
через сферическую |
|
|
|||||
поверхность достаточно просто, так как на- |
|
q |
||||||
пряжённость электрического поля в каждой |
|
|||||||
|
|
|||||||
точке поверхности направлена ортогонально |
|
Рис. 1.3 |
||||||
к ней и одинакова по модулю: |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
E = |
1 |
|
|
q |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
4πε0 (2R )2 . |
|
|
||||
Учитывая это, получаем:
Φ E сф = E Sсф .
Площадь сферической поверхности можно определить по формуле:
Sсф = 2πr 2 (1− cos α) ,
Sсф
S
(1.5)
(1.6)
(1.7)
где r = 2R – радиус сферической поверхности. Из рис. 1.3 видно, что α = 30º,
cos α = |
3 |
. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
q |
|
2π (2R ) |
2 |
3 |
q |
3 |
|
||||||||
|
|
Φ |
E сф |
= |
|
|
|
|
|
1− |
|
|
|
= |
|
1− |
|
|
|
|
(1.8) |
||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
4πε0 |
|
(2R ) |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2ε0 |
2 |
|
|
|
|||||
Таким образом,
15

|
|
|
|
|
|
|
|
|
10−9 |
|
|
|
|
|
|
q |
3 |
|
|
|
|||||
Φ |
E |
= − |
|
1 − |
|
|
|
= − |
|
|
0,134 = −7, 57 В м. |
(1.9) |
|
|
|
|
|
−12 |
|||||||
|
|
2ε0 |
|
2 |
|
|
2 8, 85 10 |
|
||||
|
|
|
|
|
|
|
|
|
||||
Знак «–» в (1.9) означает, что силовые линии электрического поля входят внутрь замкнутой поверхности S0 там, где находится круг S. Для незамкнутой поверхности S этот знак значения не имеет, поэтому в ответе его учитывать не будем.
Ответ: Φ E = 7, 57 В м.
Задача 2. Внутри воздушного шара находится N = 106 торых имеет заряд q= –1,6 10–19 Кл. Определить поток ΦE электрического поля через поверхность шара.
Решение. Поток вектора напряжённости электрического ΦE через поверхность шара S можно определить с помощью теоремы Гаусса:
пылинок, каждая из ковектора напряжённости
S
|
|
|
|
|
|
|
|
N |
|
|
|
|
ΦE = ∫∫ |
|
|
|
|
∑qi |
|
|
E |
||||
|
|
i =1 |
|
|
|
|
||||||
EidS = |
. |
(2.1) |
|
|||||||||
|
|
|||||||||||
|
S |
|
|
|
|
|
|
ε0 |
|
|
|
|
Необходимо учесть только те заряды, которые нахо- |
|
|||||||||||
дятся внутри шара: |
|
|
|
|
|
|
|
|
|
|
|
|
ΦE = |
q N |
= |
−1, 6 10−19 106 |
= −0, 018 В м. |
(2.2) |
|||||||
ε |
|
|
|
|
8, 85 10 |
−12 |
||||||
|
0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: Φ E = −0, 018 В м.
Задача 3. Равномерно заряженная с линейной плотностью τ = 1 нКл/м прямая проволока окружена облаком электронов, которое имеет вид коаксиального длинного цилиндра радиусом R = 5 мм. Считая, что заряд облака распределён равномерно и линейная плотность его равна –τ, определить напряжённость электрического поля в точках, удалённых на расстояние r1 = 2 мм и r2 = 7 мм от нити.
Решение. Распределение зарядов в пространстве имеет осесимметричный характер. Значит электрическое поле, порождаемое этими зарядами, будет иметь такой же характер симметрии. Силовые линии напряжённости электрического поля будут исходить из проволоки в радиальном направлении. Учитывая это, для решения задачи можно воспользоваться теоремой Гаусса. Необходимо выделить замкнутую поверхность, через которую будет удобно рассчитывать поток ΦE.
16

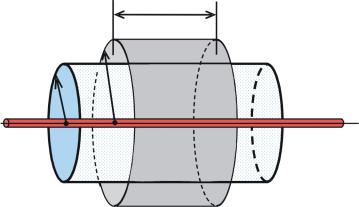
1)Это может быть коаксиальная цилиндрическая поверхность S1 радиусом r1
ивысотой h, погружённая полностью в облако заряда (рис. 3.1). Ненулевой поток
ΦE будет проходить только через |
|
|
|
–τ |
||||
боковую |
поверхность, причём |
|
|
ρ |
||||
вектор E |
|
|
|
R |
|
S1 |
|
|
будет перпендикулярен |
r1 |
|
|
+τ |
||||
каждому |
элементу |
цилиндриче- |
|
|
||||
|
|
|
|
|||||
ской поверхности и будет одина- |
|
|
|
|
||||
ковым по модулю на всей боковой |
|
h |
|
|
||||
поверхности. Значит, определить |
|
|
|
|
||||
поток через эту поверхность мож- |
|
Рис. 3.1 |
|
|
||||
но следующим образом: |
|
|
|
|||||
|
|
|
|
|||||
|
|
ΦE = ∫∫ EidS = E1 Sбок = E1 2πr1h, |
|
|
(3.1) |
|||
|
|
|
|
S1 |
|
|
|
|
где E1 – напряжённость электрического поля на цилиндрической поверхности |
||||||||
(рис. 3.2). Поток через основания цилиндра |
E |
|
|
|
||||
будет равен нулю, |
поскольку напряжён- |
|
Sбок |
dS |
||||
|
|
|
|
|
|
|
E1 |
|
ность поля перпендикулярна нормали к по- |
n |
|
|
|
||||
верхности. |
|
|
|
|
||||
|
|
|
|
|
||||
Согласно теореме Гаусса: |
|
|
|
|
||||
|
|
N |
|
|
|
|
|
|
|
|
∑qi |
|
Sосн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ΦE = |
i =1 |
. |
(3.2) |
|
|
Рис. 3.2 |
|
|
|
|
|
|||||
|
|
ε0 |
|
|
|
|
|
|
В этой сумме необходимо учитывать только те заряды, которые находятся внутри выбранной замкнутой цилиндрической поверхности S1, то есть часть заряда проволоки и часть окружающего её пространственного заряда:
N |
|
∑qi = τh + ρVцил , |
(3.3) |
i =1
где ρ – объёмная плотность заряда облака электронов, Vцил = πr12h – объём, заключённый внутри замкнутой цилиндрической поверхности S1. Если выбрать часть облака электронов длиной l, то заряд его будет равен:
|
|
q = −τ h = ρ πR2 h. |
|
|
|
|
(3.4) |
||||||
Отсюда, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ = − τ πR2 . |
|
|
|
|
|
|
|
(3.5) |
||||
Подставляя (3.3) и (3.5) в (3.2), получаем: |
|
|
|
|
|
|
|
|
|||||
|
τ h − |
τ |
|
πr 2 h |
|
|
|
|
2 |
|
|
||
|
|
|
τh |
r |
|
||||||||
|
|
πR |
2 |
1 |
|
|
|
|
|
||||
ΦE = |
|
|
|
|
= |
|
1− |
1 |
|
. |
(3.6) |
||
|
ε0 |
|
|
|
ε0 |
R |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
||||
17
Приравниваем (3.1) и (3.6):
|
|
τh |
|
r 2 |
|
|
E 2πr h = |
|
1− |
1 |
. |
(3.7) |
|
|
|
|||||
1 |
1 |
ε0 |
|
R2 |
|
|
Таким образом, напряжённость электрического поля на расстоянии r1 = 2 мм от проволоки равна:
|
|
τ |
|
r 2 |
|
10−9 |
|
|
|
|
2 2 |
В |
|
|||||
E1 |
= |
|
1− |
1 |
|
= |
|
|
|
|
1− |
|
|
= 7560 |
|
. |
(3.8) |
|
2πε r |
R |
2 |
2π 8, 85 10 |
−12 |
2 10 |
−3 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
5 |
|
м |
|
||||||
|
|
0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) Аналогично определим напряжённость электрического поля E2 на расстоянии r2 = 7 мм от проволоки. Для этого выберем замкнутую цилиндрическую поверхность S2 радиусом r2 и высотой h (рис. 3.3). Поток ΦE определяется аналогично предыдущему случаю:
|
|
|
|
|
|
Φ E = ∫∫ E idS = E2 Sбок = E2 2πr2 h. |
|
(3.9) |
|||
|
S2 |
|
|
|
|
Для того чтобы применить тео- |
h |
|
|
||
рему Гаусса (3.2), необходимо оп- |
|
|
|||
|
|
|
|||
ределить сумму зарядов, |
находя- |
r2 |
S2 |
|
|
щихся внутри поверхности S2. Эта |
|
||||
|
|
||||
R |
|
–τ |
|||
сумма будет включать в себя заряд |
ρ |
||||
|
|
||||
части проволоки τh и заряд части |
|
|
+τ |
||
облака –τh: |
|
|
|
||
|
|
|
|
||
N |
|
|
|
|
|
∑qi = τh − τh = 0. |
(3.10) |
|
|
|
|
i =1
Следовательно, поток ΦE через по-
Рис. 3.3
верхность S2 равен нулю, а значит
E2 = 0.
Ответ: E1 = 7560 В/м; E2 = 0.
Задача 4. В модели атома Томсона предполагалось, что положительный заряд q = +e распределён внутри шара радиусом R = 10–10 м. Как должна зависеть объёмная плотность ρ(r) положительного заряда от расстояния до центра шара r, чтобы электрон, помещённый внутри шара, мог совершать гармонические колебания? Найти частоту колебаний электрона.
Решение. В модели атома Томсона ядро отсутствует, а весь положительный заряд представляет собой облако с объёмной плотностью ρ, внутри которого летает электрон, так что атом должен быть электрически нейтральным.
18
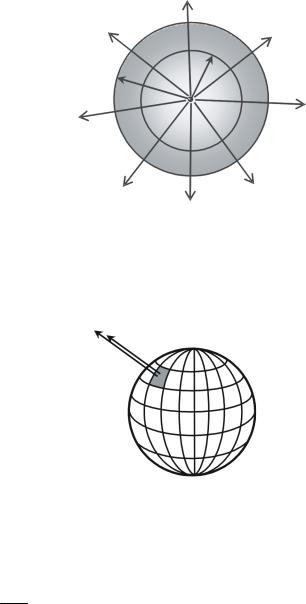
1) Будем полагать, что облако положительного заряда сферически симметричное и его объёмная плотность одинаковая во всей области радиусом R. Определим распределение напряжённости электрического поля внутри атома E(r). Если распределение заряда имеет сферическую или центральную симметрию, то и электрическое поле, порождаемое им, будет иметь такой же тип симметрии. Силовые линии напряжённости электрического поля будут исходить из центра ато-
ма во всех направлениях радиально. Учитывая |
|
|
|
симметрию поля, можно воспользоваться тео- |
|
|
|
ремой Гаусса для определения напряжённости |
|
r |
|
поля E на расстоянии r от центра. Для этого вы- |
|
||
|
ρ |
||
берем замкнутую поверхность S – концентриче- |
|
||
R |
|||
скую сферу, лежащую внутри атома (рис. 4.1). |
E |
||
|
S |
||
На всей поверхности сферы S напряжённость |
|
||
|
|
||
будет направлена перпендикулярно к каждому |
|
|
|
элементу поверхности и будет одинакова по |
|
|
|
модулю (рис. 4.2). Поэтому, определить поток |
|
|
|
ΦE через такую поверхность можно по формуле: |
|
Рис. 4.1 |
Φ E = ∫∫ EidS = E (r ) Sсф = E (r ) 4πr 2 .
|
|
|
|
|
|
S |
|
|
|
|
|
|
Для того чтобы |
воспользоваться |
теоремой |
|
|||||||||
Гаусса (3.2), необходимо определить заряд, |
||||||||||||
dS |
||||||||||||
заключённый внутри замкнутой поверхности: |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
E |
|
q = ρVшара = ρ |
4π |
r |
3 |
. |
(4.2) |
|
||||||
3 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
По теореме Гаусса: |
|
|
|
|
|
|
|
|
|
|||
ΦE = |
q |
= ρ |
|
4π |
r3 . |
|
(4.3) |
|
||||
|
|
|
|
|||||||||
|
ε0 |
|
3ε0 |
|
|
|
|
|
||||
Приравниваем (4.1) и (4.3):
E (r ) 4πr 2 = ρ 4π r 3. 3ε0
Отсюда получаем:
(4.1)
S
(4.4)
E (r ) = |
ρ |
r. |
(4.5) |
|
|||
|
3ε0 |
|
|
Напряжённость электрического поля внутри атома Томсона равномерно возрастает от центра к границе. Значит кулоновская сила, действующая на электрон,
19
