СМОЛЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Г. С. ЕВДОКИМОВА

ПРАКТИКУМ

ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКОЙ

СТАТИСТИКЕ

МОДУЛЬ 1

НЕПОСРЕДСТВЕННОЕ ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТЕЙ

Смоленск 2009

Множество элементарных исходов будем обозначать через

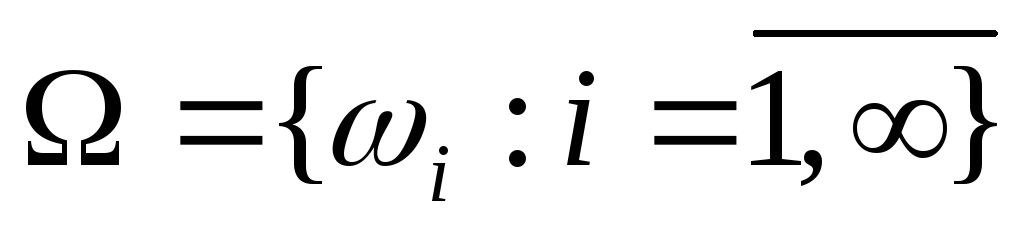
При классическом определении вероятность события определяется равенством

,

где m - число элементарных исходов испытания, благоприятствующих появлению события А; n – общее число возможных элементарных исходов испытания.

Пусть А_i (i = 1,2,…,n) – элементы конечного множества.

Правило суммы. Если элемент А₁ может быть выбран n₁ способами, элемент А₂ – другими n₂ способами, А₃ – отличными от первых двух n₃ способами и т. д., А_k – n_k способами, отличными от первых (k – 1), то выбор одного из элементов: или А₁, или А₂,…, или А_k может быть осуществлён n₁+n₂+…+n_k способами.

Правило произведения. Если элемент А₁ может быть выбран n₁ способами, после каждого такого выбора элемент А₂ может быть выбран n₂ способами и т. д., после каждого (k - 1) выбора элемент А_k может быть выбран n_k способами, то выбор всех элементов A₁, A₂,…,A_k в указанном порядке может быть осуществлён n₁ n₂…n_k способами.

Для вычисления числа благоприятствующих рассматриваемому событию исходов или общего числа элементарных исходов широко используются правила и формулы комбинаторики.

Если составляются такие комбинации из n элементов по m, которые отличаются друг от друга только составом элементов, то они называются сочетаниями. Общее число сочетаний из n элементов по m определяется по формуле

Если комбинации отличаются не только составом элементов, но и порядком их следования, то они называются размещениями. Их число находится по формуле

Если комбинации берутся из всех n элементов и отличаются только порядком следования элементов, то они называются перестановками. Их число равно

.

Если в размещениях (сочетаниях) из n элементов по m некоторые из элементов (или все) могут оказаться одинаковыми, то такие размещения (сочетания) называются размещениями (сочетаниями) с повторениями из n элементов по m.

Число размещений с повторениями из n элементов по m равно

а число сочетаний с повторениями из n элементов по m равно

Если в перестановках из общего числа n элементов есть k различных элементов, при этом 1-й элемент повторяется n₁ раз, 2-й элемент – n₂ раз, k-й элемент – n_k раз, причём n₁+n₂+…+n_k=n, то такие перестановки называют перестановками с повторениями из n элементов. Число перестановок с повторениями из n элементов равно

Относительная частота события А определяется равенством

где m – число испытаний, в которых событие A наступило; n – общее число произведённых испытаний.

При статистическом определении в качестве вероятности события принимают его относительную частоту.

Геометрической вероятностью события называется отношение меры области, благоприятствующей появлению события A, к мере всей области

где mes – мера (длинна, площадь, объём) области.

Цель занятия: 1.Освоение понятий: элементарное событие, случайное событие, пространство элементарных событий.

2. Научить студента при подборе необходимой комбинаторной формулы пользоваться схемой:

Откуда выбор? Какой выбор? Что нас интересует

(n-?) при выборе?

Сколько выбираем? ПовторныйСостав

(r-?) Состав

Бесповторный и порядок

3. Добиться усвоения классического определения вероятности и свойств вероятностей.

К занятию по данной теме должны быть подготовлены ответы на следующие вопросы:

1. Существуют ли закономерности у случайных событий?

2. Являются ли понятия закономерность и случайность взаимно исключающими?

3. Что является мерой объективной возможности наступления события?

4. В каком случае может быть произведен непосредственный подсчет вероятностей? Каким образом?

При решении каждой из задач следует обращать внимание студентов на условия, при которых применимо классическое определение вероятности, т.е., на равновозможность исходов и на то, как она может быть обеспечена. Полезно истолкование каждого результата в частотном смысле. Например, если Р =1/3, то это означает, что в каждой достаточно большой серии опытов примерно 1/3 их часть закончится появлением данного события.

Задача 1. Брошена один раз игральная кость. Пусть Х – число очков, выпавших на верхней грани. Описать множество элементарных исходов Ω и указать подмножества, соответствующие следующим событиям:

А={Х кратно трем},

В={Х нечетно},

С={Х >3},

D={Х <7},

Е={Х дробно},

F={0.5<Х<1.5}.

Выявить пары совместных событий.

Решение.

, ,, , , , .

Совместные события: А и В, А и С, А и D, В и С, В и D, В и F, С и D , D и F.

Задача 2. В ящике 300 деталей. Известно, что 150 из них – 1-го сорта, 120 – 2-го, а остальные 3-го сорта. Сколько существует способов извлечения из ящика одной детали 1-го Ии 2-го сорта?

Решение. Деталь 1-го сорта может быть извлечена n₁=150 способами, 2-го сорта – n₂ =120 способами. По правилу суммы существует n₁+n₂ = 150+120=270 способов извлечения одной детали 1-го или 2-го сорта.

Задача 3. В группе 30 человек. Необходимо выбрать старосту, его заместителя и профорга. Сколько существует способов это сделать?

Решение. Старостой может быть выбран любой из 30 учащихся, его заместителем – любой из оставшихся 29, а профоргом - любой из оставшихся 28 учащихся, т. е. n₁=30, n₂=29, n₃=28. По правилу произведения общее число способов выбора старосты, его заместителя и профорга равно n₁n₂n₃ = 30∙29∙28 = =24360 способов.

Задача 4. Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин.

Решение. Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающихся от других вариантов, как составом дисциплин, так и порядком их следования (или и тем, и другим), т.е. является размещением из 11 элементов по 5. Число вариантов расписания будет:

Задача 5. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?

Решение. Каждая партия играется двумя участниками из 16 и отличается от других только составом пар участников, т.е. представляет собой сочетание из 16 элементов по 2. Их число равно:

Задача 6. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьёвки при этом возможно?

Решение. Каждый вариант жеребьёвки отличается только порядком участников конкурса, т.е. является перестановкой из 7 элементов. Их число:

Задача 7. В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует вариантов распределения призов, если по каждой номинации установлены: а) различные призы; б) одинаковые призы?

Решение. а) Каждый из вариантов распределения призов представляет собой комбинацию 5 фильмов из 10, отличающихся от других комбинаций, как составом фильмов, так и их порядком по номинациям (или и тем, и другим), причём одни и те же фильмы могут повторяться несколько раз (любой фильм может получить призы как по одной, так и по нескольким номинациям), т.е. представляет размещение с повторениями из 10 элементов по 5. Их число равно:

б) Если по каждой номинации установлены одинаковые призы, то порядок следования фильмов в комбинации 5 призёров значения не имеет, и число вариантов распределения призов представляет собой число сочетаний с повторениями из 10 элементов по 5:

Задача 8. Сколько существует семизначных чисел, состоящих из цифр 4,5 и 6, в которых цифра 4 повторяется 3 раза, а цифры 5 и 6 – по 2 раза?

Решение. Каждое семизначное число отличается от другого порядком следования цифр (причём n₁=3, n₂=2, n₃=2, а их сумма равна 7), т.е. является перестановкой с повторениями из 7 элементов. Их число:

Задача 9. Брошены две игральные кости. Найти вероятности следующих событий:

А – на обеих костях выпало одинаковое число очков;

В – число очков на первой кости больше, чем на второй;

С – сумма очков четная;

D – сумма очков больше двух.

Решение. Число исходов, благоприятствующих каждому из событий, легко подсчитать, если все возможные исходы опыта перечислить в виде таблицы. В каждой клетке табл.1 первая цифра указывает число очков на первой кости, вторая – на второй. Непосредственный подсчет числа исходов дает

,

Таблица 1

11	12	13	14	15	16
21	22	23	24	25	26
31	32	33	34	35	36
41	42	43	44	45	46
51	52	53	54	55	56
61	62	63	64	65	66

Задача 10. Буквы Т, Е, И, Я, Р, О написаны на отдельных карточках. Ребёнок берёт карточки в случайном порядке и прикладывает одну к другой: а) 3 карточки; б) все 6 карточек. Какова вероятность того, что получится слово: а) «ТОР»; б) «ТЕОРИЯ»?

Решение. Пусть событие A – получение слова «ТОР». Различные комбинации трёх букв из имеющихся шести представляют размещения, так как могут отличаться как составом входящих букв, так и порядком их следования (или и тем, и другим), т.е. обще число случаев , из которых благоприятствуют событиюA m=1 случай. По формуле:

б) Пусть событие В – получение слова «ТЕОРИЯ». Различные комбинации шести букв из имеющихся шести представляют собой перестановки, так как отличаются только порядком следования букв; т.е. общее число случаев n = P₆ = 6!, из которых благоприятствует событию B m=1 случай. Поэтому

Задача 11. Используя условие задачи 10, найти вероятность того, что получится слово «АНАНАС», если на отдельных карточках написаны три буквы А, две буквы Н и одна буква С.

Решение. Пусть событие B – получение слова «АНАНАС». Так же, как и в задаче 10 б, общее число случаев n = P₆ = 6!, но теперь число случаев m, благоприятствующих событию B, существенно больше, так как перестановка трех букв A, осуществляемая P₃=3! способами, и перестановка двух букв Н (P₂ = 2! способами) не меняет собранное из карточек слово «АНАНАС»; по правилу произведения m=P₃∙P₂.

Итак,

(Задачу можно решить и иначе, рассматривая комбинации букв как перестановки с повторениями, из которых событию B благоприятствует 1 комбинация:

Задача 12. Из 30 студентов 10 имеют спортивные разряды. Какова вероятность того, что выбранные наудачу 3 студента - разрядники?

Решение. Пусть событие А – 3 выбранных наудачу студента - разрядники. Общее число случаев выбора 3 студентов из 30 равно так как комбинации из 30 студентов по 3 представляют собой сочетания, ибо отличаются только составом студентов. Точно так же число случаев, благоприятствующих событиюA, равно Итак,

Задача 13. В лифт на 1-м этаже девятиэтажного дома вошли 4 человека, каждый из которых может выйти независимо друг от друга на любом этаже с 2-го по 9-й. Какова вероятность того, что все пассажиры выйдут: а) на 6-м этаже; б) на одном этаже?

Решение. а) Пусть событие А – все пассажиры выйдут на 6-м этаже. Каждый пассажир может выйти со 2-го по 9-й этаж 8 способами. По правилу произведения обще число способов выхода четырёх пассажиров из лифта равно n = 8∙8∙8∙ 8 = 8⁴. Число случаев, благоприятствующих событию А, равно m=1. Таким образом,

б) Пусть событие В – все пассажиры выйдут на одном этаже. Теперь событию В будут благоприятствовать m=8 случаев (все пассажиры выйдут или на 2-м этаже, или на 3-м,…, или на 9-м этаже). Поэтому

(Общее число способов выхода пассажиров из лифта можно найти иначе, если учесть, что комбинации номеров этажей, на которых может выйти из лифта каждый из четырёх пассажиров, например, 3456, 4356, 4433, 5666, 5555, 9785 и т.д., представляют собой размещение с повторениями из 8 элементов (этажей) по 4. Их число равно ).

Задача 14. По условиям лотереи «Спортлото 6 из 45» участник лотереи, угадавший 4,5,6 видов спорта из отобранных при случайном розыгрыше 6 видов спорта из 45, получает денежный приз. Найти вероятность того, что будут угаданы: а) все 6 цифр; б) 4 цифры.

Решение. а) Пусть событие A – угадывание всех 6 видов спорта из 45. Общее число всех случаев, т.е. всех вариантов заполнения карточек спортлото, есть , так как каждый вариант заполнения отличается только составом видов спорта. Число случаев, благоприятствующих событиюА, есть m=1. Поэтому

б) Пусть событие В – угадывание 4 видов спорта из 6 выигравших из 45. Вначале найдем число способов, какими можно выбрать 4 вида спорта из 6 выигравших, т.е. . Но это ёще не всё: к каждой комбинации 4-х выигравших видов спорта из 6 следует присоединить комбинацию 2-х невыигравших видов из 45–6=39; таких комбинацийПо правилу произведения обще число случаев, благоприятствующих событиюВ, равно Итак,

Задача 15. В партии 100 изделий, из которых 4 – бракованные. Партия произвольно разделена на две равные части, которые отправлены двум потребителям. Какова вероятность того, что все бракованные изделия достанутся: а) одному потребителю; б) обоим потребителям поровну?

Решение. Пусть событие А – все бракованные изделия достанутся одному потребителю. Общее число способов, какими можно выбрать 50 изделий из 100, равно СобытиюА благоприятствуют случаи, когда из 50 изделий, отправленных одному потребителю, будет либо 46 стандартных из 96 (и все 4 бракованных) изделий, либо 50 стандартных из 96 (и 0 бракованных); их число Поэтому

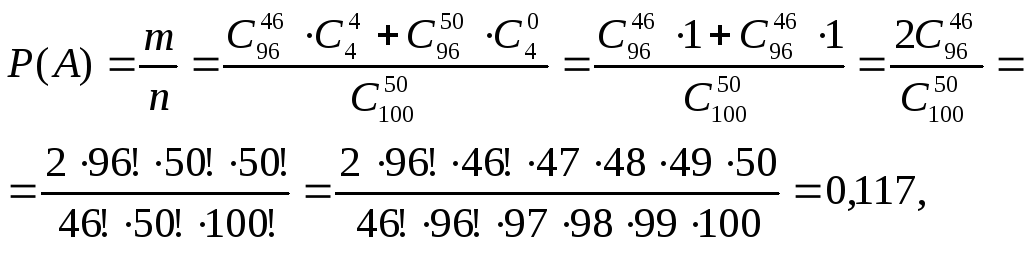
где 100! = 96! ∙ 97 ∙ 98 ∙ 99 ∙ 100, 50! = 46! ∙ 47 ∙ 48 ∙ 49 ∙ 50.

б) Пусть событие В – в каждой партии по 2 бракованных изделия. Теперь событию В будут благоприятствовать случаи, когда из 50 изделий, отправленных одному потребителю, будут 48 стандартных из 96 и 2 бракованных из 4, их число Поэтому

Задача 16. В магазине было продано 21 из 25 холодильников трёх марок, имеющихся в количествах 5, 7 и 13 штук. Полагая, что вероятность быть проданным для холодильника каждой марки одна и та же, найти вероятность того, что остались нераспроданными холодильники: а) одной марки; б) трех разных марок.

Решение. а) Пусть событие А – остались нераспроданными холодильники одной марки. Общее число способов, которыми можно получить 4 (непроданных) холодильника из 25, равно . Число способов, которыми можно получить 4 холодильника первой марки из 5, равно; второй марки изи третьей марки изСобытиюА по правилу суммы благоприятствует m = m₁ + m₂ + m₃ = случаев. Поэтому

б) Пусть событие В – остались непроданными холодильники трех разных марок. Событие В может произойти по одному из трёх вариантов. По первому варианту событие В произойдёт, если останутся нераспроданными 1, 1, 2 холодильников соответственно 1-й, 2-й и 3-й марок; по второму варианту – 1, 2, 1 и по третьему варианту останутся нераспроданными 2, 1, 1 холодильников соответственно 1-й, 2-й и 3-й марок. Так как до подажи имелось 5 холодильников 1-й марки, 7 – 2-й и 13 холодильников 3-й марки, то по правилу произведения число случаев, благоприятствующих первому варианту, равно второму –третьему варианту –Общее число случаев, благоприятствующих событиюВ, равно m=m₁+m₂+m₃. Теперь

Задача 17. Из партии, содержащей 10 изделий, среди которых 3 бракованных, «наудачу» извлекают три изделия для контроля. Найти вероятность следующих событий:

А - среди выбранных изделий ровно два бракованных;

В – выбраны все бракованные изделия;

С – среди выбранных изделий содержится хотя бы одно бракованное.

Решение. Выбрать любых три изделия из 10 можно способами. Поэтому имеем равновозможных исходов.

1. Событию А благоприятствуют те исходы, при которых из 7 годных изделий выбирается одно (это можно сделать способами) и из трех бракованных 2 (это можно сделатьспособами). По комбинаторному принципу число благоприятствующих событиюА исходов равно

.

Поэтому , т.е. примерно один шанс из шести.

2. Событию В благоприятствуют исходов и его вероятность.

3. Вероятность события С проще вычислять, определив вероятность события , которое состоит в том, что выбраны все годные изделия. Выбрать три годных изделия из семи можноспособами. Поэтому

и

Задача 18. Каждый из пяти студентов может сдавать зачет по выбору в один из пяти назначенных дней. Выбор каждым студентом любого дня равновозможен. Какова вероятность того, что каждый день на зачет будет приходить только один студент? Если студентов 3, а дней зачета 5, то какова вероятность того, что эти три студента явятся в разные дни?

Решение. Каждый из студентов может выбрать любой из 5 дней, поэтому по дням явки на зачет они могут распределиться 5 способами. Благоприятствующие способы можно перебрать, если распределить студентов по одному на каждый день и взять всевозможные перестановки студентов. Таких перестановок будети вероятность явки по одному каждый день равна. Если студентов 3, то возможных способов явки, а благоприятствующих способов

(первый является в любой из 5дней, второй - в любой из оставшихся 4, третий – в любой из оставшихся 3 дней).

Вероятность интересующего нас события

Задача 19. На отрезок ОА длины L числовой оси брошены «наугад» две точки В и С, причем точка С расположена правее В. Найти вероятность того, что длина отрезка ВС меньше длины отрезка ОВ.

O B C A

Предполагается, что вероятность попадания точки на отрезок пропорциональна длине этого отрезка и не зависит от его расположения на числовой оси.

Решение. Обозначим через и координаты точекВ и С соответственно. Координаты точек В и С должны удовлетворять неравенствам , Указанным неравенствам удовлетворяют координаты любой точки ∆ ОКМ.

y

K N

M

O x

Рис. 1

Длина отрезка ВС должна быть меньше ОВ, т.е. у –х < х или у < 2х, т.е. фигурой, координаты точек которой благоприятствуют этому событию, является треугольник ОNM (рис.1). Поэтому искомая вероятность

Дополнительные задачи.

Задача 1. Десять команд случайным образом разбиваются на две равные группы. Какова вероятность того, что две сильнейшие команды попадут в разные группы?…в одну группу?

Ответ:

Задача 2. Из полной колоды карт (52 шт.) наугад выбраны 3 карты. Какова вероятность того, что это «тройка», «семерка», «туз»?

Ответ:

Задача 3. Придумать случайное событие, имеющее вероятность 3/7.

Задача 4. В старинной игре в кости необходимо было для выигрыша получить при бросании трех игральных костей сумму очков, превосходящую 10. Найти вероятность: а) выпадения 10 очков; б) выигрыша?

Ответ: а) 0,125; б) 0,5.

Задача 5. Сигнал воздушного оповещения от радиолокационного поста может появиться с одинаковой вероятностью в любой момент времени между и . Найти вероятность того, что он появится в интервале,считая.Сигнал полагаем точечным, т.е. пренебрежимо малым по длительности по сравнению с интервалом.

Ответ: р =().

Задача 6. Множество Е содержит 10 первых букв русского алфавита. Сколько различных алфавитов из трех букв можно составить из данного множества букв? Какова вероятность того, что случайно выбранный алфавит будет содержать букву а?

Решение. Число различных алфавитов равно числу 3-элементных подмножеств множества Е (числу сочетаний из 10 элементов по 3):

Событие А ={случайно выбранный алфавит из трех букв содержит букву а}. Число элементов множества А равно числу всех возможных способов отобрать две буквы из девяти (из десяти букв исключена буква а, входящая в состав А), т.е. равно числу сочетаний из 9 элементов по 2:

Таким образом,

Задача 7. Группа, состоящая из 8 человек, занимает места за круглым столом в случайном порядке. Какова вероятность того, что при этом два определенных лица окажутся сидящими рядом?

Решение. Так как упорядочивается множество из 8 элементов, то . СобытиюА благоприятствуют такие размещения, когда два отмеченных лица сидят рядом: всего 8 различных соседних пар мест за круглым столом, на каждой из которых отмеченные лица могут сесть двумя способами, при этом остальные 6 человек размещаются на оставшиеся места произвольно, поэтому по формуле о числе элементов прямого произведения множеств получаем и

Задача 8. Пусть множество Е то же, что и в задаче 6. Опыт состоит в выборе без возвращения 4 букв и записи слова в порядке поступления букв. Сколько 4-буквенных слов может быть получено в данном опыте? Какова вероятность того, что наудачу составленное слово будет оканчиваться буквой а?

Решение. п – число всех 4-буквенных слов в данном опыте – равно числу 4-элементных упорядоченных подмножеств из 10 элементов, т.е. n =

Пусть событие А = {наудачу составленное слово из 4 букв множества Е оканчивается буквой а}. Число элементов множества А равно числу способов разместить на три оставшихся места по одному символу из 9 (символ а исключен из рассмотрения, поскольку его место уже определено); таким образом,

.

Задача 9. В технической библиотеке имеются книги по математике, физике, химии и т. д., всего по 16 разделам науки. Поступили очередные четыре заказа на литературу. Считая, что любой состав заказанной литературы равновозможен, найти вероятности следующих событий:

А = {заказаны книги из различных разделов науки},

В ={заказаны книги из одного и того же раздела науки}.

Решение. Число всех равновероятных исходов данного эксперимента равно числу сочетаний с повторениями из 16 элементов по 4, т.е. .

Число исходов, благоприятствующих событию А, равно числу способов отбора без возвращения четырех элементов из 16, поэтому

Число исходов, благоприятствующих событию В, равно числу способов выбрать один элемент из шестнадцати, поэтому

Задача 10. Опыт состоит в четырехкратном выборе с возвращением одной из букв алфавита Е= {а,б,к,о,м} и выкладывании слова в порядке поступления букв. Какова вероятность того, что в результате будет выложено слово мама?

Решение. Число элементов множества равновероятных исходов равно числу размещений с повторениями из 5 элементов по 4, т. е. n = 5⁴

Слову мама соответствует лишь один возможный исход. Поэтому

Задача 11. Семь одинаковых шариков случайным образом рассыпаются по 4 лункам (в одну лунку может поместиться любое число шариков). Сколько существует различных способов распределения 7 шариков по 4 лункам? Какова вероятность того, что в результате данного опыта первая лунка окажется пустой (при этом может оказаться пустой и еще какая-либо лунка)?

Решение. Занумеруем лунки и шарики. Можно считать, что опыт состоит в 7-кратном выборе с возвращением номера лунки и записи 7-буквенного слова. При этом каждому порядковому номеру буквы (номеру шарика) будет поставлена в соответствие одна из четырех букв алфавита (номер лунки).

Так, например, слово

1

1

3

1

4

4

2

1 2 3 4 5 6 7

означает, что в первую лунку попали шары №1, №2 и №4, во вторую лунку – шар №7, в третью – шар №3, в четвертую – шары №5 и №6. Таким образом, число всех способов распределить 7 шариков по 4 лункам равно числу различных 7-буквенных слов из алфавита в 4 буквы, т.е.

Событие А = {первая лунка окажется пустой} соответствует такому выбору, когда символ 1 (номер первой лунки) удален из алфавита. Поэтому

Задача 12. Десять приезжих мужчин, среди которых Петров и Иванов, размещаются в гостинице в два трехместных и один четырехместный номер. Сколько существует способов их размещения? Какова вероятность того, что Петров и Иванов попадут в четырехместный номер?

Решение.

Событие А ={Петров и Иванов попадут в один четырехместный номер}.

Искомая вероятность

Задача 13. Студент знает 20 из 25 вопросов программы. Зачёт считается сданным, если студент ответит не менее чем на 3 из 4 поставленных в билете вопросов. Взглянув на первый вопрос билета, студент обнаружил, что он его знает. Какова вероятность того, что студент: а) сдаст зачёт; б) не сдаст зачёт?

Ответ: а) б)

Домашнее задание.

Задача 1. В магазин поступило 30 холодильников, пять из них имеют заводской дефект. Случайным образом выбирается один холодильник. Какова вероятность того, что он будет без дефекта?

Задача 2. В коробке находится шесть одинаковых по форме и близких по диаметру сверл. Случайным образом свёрла извлекаются из коробки. Какова вероятность того, что свёрла извлекутся в порядке возрастания их диаметра?

Задача 3. Комиссия по качеству раз в месяц проверяет качество продуктов в двух из 30 магазинов, среди которых находятся и два известных вам магазина. Какова вероятность того, что в течение месяца они будут проверены?

Задача 4. На станцию прибыли 10 вагонов разной продукции. Вагоны помечены номерами от одного до десяти. Найти вероятность того, что среди пяти выбранных для контрольного вскрытия вагонов окажутся вагоны с номерами 2 и 5?

Задача 5. Изготовлена партия из 200 изделий, в которой оказалось три бракованных. Произведена выборка из пяти изделий. Найти вероятность следующих событий:

а) в выборке не будет ни одного бракованного изделия;

б) в выборке будет одно бракованное изделие?

Задача 6. Из 20 акционерных обществ (АО) четыре являются банкротами. Гражданин приобрёл по одной акции шести АО. Какова вероятность того, что среди купленных акций две окажутся акциями банкротов?

Задача 7. Из 100 изготовленных деталей 10 имеют дефект. Для проверки были отобраны пять деталей. Какова вероятность того, что среди выбранных деталей две окажутся бракованными?

Задача 8. На склад привезли 50 ящиков комплектующих изделий для одного из видов ЭВМ, но среди них оказалось четыре ящика для другого вида ЭВМ. Наудачу взяли шесть ящиков. Найти вероятность того, что в одном из этих шести ящиков окажутся некомплектные детали.

Задача 9. В партии из 15 однотипных стиральных машин пять машин изготовлены на заводе А, а 10 – на заводе В. Случайным образом отобрано 5 машин. Найти вероятность того, что две из них изготовлены на заводе А.

Задача 10. Какова вероятность того, что наудачу брошенная в круг точка окажется внутри вписанного в него квадрата.

Ответы: 1) Р = 5/6. 2) Р = 1/720. 3) Р = 0,0023. 4) Р =2/9. 5) а) Р = 0,926; б) Р = 0,072; 6) Р = 0,28 7) Р = 0,07. 8) Р = 0,345. 9) Р= = 0,38. 10) Р = 2/π ≈ 0,637.

СМОЛЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Г. С. ЕВДОКИМОВА

ПРАКТИКУМ

ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКОЙ

СТАТИСТИКЕ

МОДУЛЬ 2

Теоремы сложения и умножения вероятностей

Смоленск 2009

Теорема сложения вероятностей несовместных событий.

Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

P(A+B)=P(A)+P(B).

Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

P(A₁+A₂+...+A_n)=P(A₁)+P(A₂)+...+P(A_n).

Теорема сложения вероятностей совместных событий.

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

P(A+B)=P(A)+P(B)-P(AB).

Теорема может быть обобщена на любое конечное число совместных событий. Например, для трех совместных событий

P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC).

Теорема умножения вероятностей.

Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

P(AB)=P(A)∙P_A(B).

В частности, для независимых событий

P(AB)=P(A)∙P(B),

т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляют в предположении, что все предыдущие события уже наступили:

P(A₁A₂A₃...A_n)=P(A₁)∙P (A₂)∙P (A₃)...P (A_n),

где P (A_n) – вероятность события A_n, вычисленная в предположении, что события A₁,A₂,...,A_n-1 наступили.

В частности, вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

P(A₁A₂...A_n)=P(A₁)P(A₂)...P(A_n).

Вероятность появления хотя бы одного события.

Пусть события A₁ , A₂ ,...,A_n независимы в совокупности, причем P(A₁)=p₁ , P(A₂)=p₂ ,...,P(A_n)=p_n ;пусть в результате испытания могут наступить все события, либо часть из них.

Вероятность наступления события А, состоящего в появлении хотя бы одного из событий A₁ , A₂ ,...,A_n ,независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий ₁, ₂,..., _n:

P(A)=1-q₁q₂...q_n.

В частности, если все n событий имеют одинаковую вероятность, равную p, то вероятность появления хотя бы одного из этих событий

P(A)=1-q₁q₂...q_n.

Цель занятия: 1. Научить студентов переводить словесные рассуждения в символическую запись с помощью следующей таблицы соответствий:

В словесных рассуждениях	Символическая запись
Или	+
И	·
не А
Равносильно	=

2. Обратить внимание на то, что перед вычислением вероятности произведения событий необходимо устанавливать их зависимость или независимость, а перед вычислением суммы событий – совместность или их несовместность.

3. Рекомендовать студентам следующий порядок решения задач:

а) обозначения событий; б) анализ взаимосвязей событий; в) вычисление вероятностей.

К занятию по данной теме должны быть подготовлены ответы на следующие вопросы:

1. Может ли сумма двух событий А и В совпадать с их произведением? Привести пример.

2. Справедливо ли в общем случае равенство

Р( А/В ) = Р( А ).

2. Если событие В представляет собой частный случай события А зависимы эти события или нет?

3. Зависимы или независимы: а) несовместные события; б) события образующие полную группу?

Задача 1. Произведено 4 выстрела по мишени. Рассмотрим следующие события:

А={одно попадание},

B={хотя бы одно попадание},

C= {два попадания},

D={три попадания},

E={четыре попадания},

F={не менее двух попаданий}.

Каким событиям равносильны следующие: а) A+B; б) AB; в) B+F; г) BF; д) C+D+E; ж) BE.

Решение. а) A+B=B; б) AB=A; в) B+F=B; г) BF=F;

д) C+D+E=F; ж) BE=E. Можно отметить, что события BE и FE совпадают.

Задача 2. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно равно 0,9. Найти вероятность того, что из 2-х проверенных изделий только одно стандартное.

Решение. Пусть событие А_i состоит в том, что i-е изделие стандартно. Из 2-х изделий будет только одно стандартно (событие B), если стандартным будет первое изделие и при этом второе не стандартно или первое не стандартно и при этом второе стандартно, т. е. B =А₁Ā₂+ Ā₁А₂ . События А₁Ā₂ и Ā₁А₂ несовместны. Поэтому Р(B) = Р(А₁Ā₂) + Р(Ā₁А₂). Так как события А₁ и А₂ независимы, то независимы и события А₁ и Ā₂, а также Ā₁ и А₂. Следовательно, Р(B)=Р(А₁)Р(Ā₂)+Р(Ā₁)Р(А₂)= =0,9 0,1+0,1 0,9= 0,18.

Задача 3. Вероятность попадания в цель при выстреле для первого, второго и третьего стрелков равны соответственно 0,3; 0,6; 0,8. Все три стрелка выстрелили в цель. Какова вероятность того, что: а) цель будет поражена? б) будет только одно попадание? в) будет два попадания? г) попадут все три стрелка? д) будет хотя бы один промах?

Решение. Обозначим через А_i событие, состоящее в попадании в цель i-го стрелка.

а) Поражение цели (событие A) равносильно появлению хотя бы одного из событий А₁ или А₂ или А₃. Поэтому А=А₁+А₂+А₃. Учитывая совместность событий, имеем

Р(A) = Р(А₁) + Р(А₂) + Р(А₃) – Р(А₁А₂) – Р(А₁А₃) – Р(А₂А₃)+ +Р(А₁А₂А₃),

а так как А_i независимы

Р(A) = 0,3 + 0,6 + 0,8 – 0,3 0,6 – 0,3 0,8 – 0,6 0,8 +

+ 0,3 0,6 0,8= 0,944.

б) Рассмотрим три случая:

1. В₁ =А₁ Ā₂ Ā₃ – первый стрелок попал в цель, и при этом второй не попал, и третий не попал.

2. В₂ = Ā₁А₂Ā₃ – в цель попал второй стрелок, и при этом не попал в цель первый, и не попал третий.

3. В₃ = Ā₁Ā₂А₃ – в цель попал третий стрелок, и при этом в цель не попал первый, и не попал второй.

Ровно одно попадание в цель (событие B) равносильно реализации хотя бы одного из событий В₁ или В_{2 ,} или В₃.

Поэтому B =А₁Ā₂Ā₃ + Ā₁А₂Ā₃ + Ā₁Ā₂А₃. В силу несовместности событий В_i и независимости событий А_i имеем

Р(B) =Р(А₁)Р(Ā₂)Р(Ā₃) + Р(Ā₁)Р(А₂)Р(Ā₃) + Р(Ā₁)Р(Ā₂)Р(А₃)= =0,3 0,4 0,2 + 0,7 0,6 0,2 + 0,7 0,4 0,8 = 0,332.

в) Два попадания в цель (событие C) равносильны реализации хотя бы одного из несовместных случаев А₁А₂Ā₃ или А₁Ā₂А₃ или Ā₁А₂А₃. Поэтому в силу независимости событий А_i

Р(C) = 0,3 0,6 0,2 + 0,3 0,4 0,8 + 0,7 0,6 0,8 = 0,468.

г) Попадут все три стрелка (событие D), если попадут первый и второй, и третий стрелок, т.е. D а так как события независимы то

.

д) Хотя бы один промах (событие E ) равносилен появлению хотя бы одного из событий или ,или , т.е. но проще заметить, что E равносильно непоявлению события D. Поэтому

Задача 4. Вероятность безотказной работы в течение заданного времени (надежность) каждого элемента равна 0,8. Из этих элементов составлены две системы:

1

2

1

2

3

4

К

3

4

Какая система надежнее? (Иначе говоря, что выгоднее дублировать в системе каждый элемент отдельно или всю систему в целом?)

Решение. Пусть событие состоит в том, чтоэлемент работает безотказно. Безотказная работа первой системы (событиеB₁) равносильна безотказной работе первого элемента и второго или третьего и четвертого. Символически эту фразу можно записать Событияисовместны, а событиянезависимы. Поэтому

Безотказная работа второй системы (событиеB₂) равносильна безотказной работе первого элемента или третьего и второго или четвертого, т.е.

т.е. выгоднее дублировать каждый элемент отдельно.

Задача 5. В одной урне 5 белых, 7 черных и 3 красных шара, во второй соответственно 4 белых, 2 черных и 4 красных. Из каждой урны вынимается наугад по одному шару. Какова вероятность того, что будут выбраны шары одного цвета?

Решение. Обозначим события – извлечение из i-й урны белого, красного и черного шара соответственно буквами ,,. Тогда извлечение шаров одного цвета (событиеA) можно символически записать следующим образом:

“и” “или” “и” “или” “и”

Так как события, образующие сумму, несовместны, то . В силу независимости событий

Задача 6. Партия деталей (100 штук) содержит 5 бракованных. Условия приема партии предусматривают проверку наугад выбранной половины партии. Если среди проверенных будет не более одной детали бракованной, то партия принимается. Какова вероятность приема партии?

Решение. Рассмотрим события:

A - среди проверенных не более одной бракованной;

B - среди проверенных нет бракованных;

C - среди проверенных одна бракованная деталь.

Событие A равносильно появлению события B или C , т. е. A=B+C. В силу несовместности событий B и C имеем P(A)=P(B)+P(C). Найдем вероятности P(B) и P(C). Из 100 деталей 50 можно выбрать способами, а из95 небракованных деталей 50 можно выбрать способами. ПоэтомуАналогичноТогдаP(A) = 0,028 + 0,153 = 0,181.

Задача 7. На перевозку груза направлены 4 автомобиля. Вероятность нахождения каждой из машин в исправном состоянии равна 0,8. Найти вероятность того, что в работе участвует хотя бы один из выделенных для этого автомобилей.

Решение. Вероятность противоположного события (машина неисправна) равна q=1-0,8=0,2. Следовательно,

P(A)=1-q⁴=1-0,2⁴=0,9984.

Задача 8. Вероятность обслуживания клиента одним операционистом в банке равна 0,6. Какое минимальное число операционистов должно работать в банке, чтобы вероятность обслуживания клиента была не менее 0,95?

Решение. Вероятность противоположного события (отказ в обслуживании клиента операционистом) равна 0,4. Пусть n-количество операционистов, удовлетворяющее условию задачи, т.е.

P(A)=1-qⁿ=1-0,4ⁿ≥0,95.

Решая это неравенство, получаем

0,4ⁿ≤0,05.

Логарифмирование обеих частей этого неравенства дает

n≥lg0,05/lg0,4=3,27.

Поскольку n должно быть целым числом, окончательно получаем, что в банке должны работать не менее четырех операционистов.

Дополнительные задачи

Задача 1. Вероятность того, что студент сдаст первый экзамен равна 0,9; второй – 0,9; третий – 0,8. Найти вероятность того, что студентом будут сданы: а) только 2-й экзамен; б) только один экзамен; в) три экзамена; г) по крайней мере два экзамена; д) хотя бы один экзамен.

Решение. а) Обозначим события: А_i – студент сдаст i-й экзамен (i=1,2,3); В – студент сдаст только 2-й экзамен из трех. Очевидно, что B=₁ A_{2 3} , т.е. совместное осуществление трех событий, состоящих в том, что студент сдаст 2-й экзамен и не сдаст 1-й и 3-й экзамены. Учитывая, что события А₁, А₂, А₃ независимы, получим

P(B)=P(₁ A_{2 3} )=P(₁)P(A₂)P(₃)=0,1∙0,9∙0,2=0,018.

б) Пусть событие С – студент сдаст один экзамен из трех. Очевидно, событие С произойдет, если студент сдаст только 1-й экзамен из трех или только 2-й, или только 3-й, т.е.

P(C)=P(A₁₂₃+₁A_{2 3}+₁₂A₃)=

=0,9∙0,1∙0,2+0,1∙0,9∙0,2+0,1∙0,1∙0,8=0,044.

в) Пусть событие D – студент сдаст все три экзамена, т.е. D=A₁A₂A₃. Тогда

P(D)=P(A₁A₂A₃)=P(A₁)P(A₂)P(A₃)=0,9∙0,9∙0,8=0,648.

г) Пусть событие Е – студент сдаст по крайней мере два экзамена (иначе: «хотя бы два экзамена» или «не менее двух экзаменов»). Очевидно, что событие Е означает сдачу любых двух экзаменов из трех или всех трех экзаменов, т.е.

E=A₁A_{2 3}+A₁₂ A₃+₁A₂ A₃+A₁A₂A₃ и

P(E)=0,9∙0,9∙0,2+0,9∙0,1∙0,8+0,1∙0,9∙0,8+0,9∙0,9∙0,8=0,954.

д) Пусть событие F – студент сдал хотя бы один экзамен (иначе: «не менее одного» экзамена). Очевидно, событие F представляет сумму событий С (включающего три варианта) и Е (четыре варианта), т.е. F=A₁+A₂+A₃=C+E (семь вариантов). Однако проще найти вероятность события F, если перейти к противоположному событию, включающему всего один вариант – F==₁+₂+₃ .

Итак,

P(F)=P(A₁+A₂+A₃)=1-P()=1-P(_{12 3})=

1-P(₁)∙P(₂)∙P(₃)=1-0,1∙0,1∙0,2=0,998,

т.е. сдача хотя бы одного экзамена из трех является событием практически достоверным.

Задача 2. Причиной разрыва электрической цепи служит выход из строя элемента К₁ или одновременный выход из строя двух элементов – К₂ и К₃. Элементы могут выйти из строя независимо друг от друга с вероятностями, равными соответственно 0,1; 0,2; 0,3. Какова вероятность разрыва электрической цепи?

Решение. Обозначим события:

A_i – выход из строя элемента K_i (i=1,2,3);

В – разрыв электрической цепи.

Очевидно, по условию событие В произойдет, если произойдет событие А₁ или А₂А₃, т.е. В=А₁+А₂А₃ .

P(B)=P(A₁+A₂A₃)=P(A₁)+P(A₂A₃)-P[A₁(A₂A₃)]=

=P(A₁)+P(A₂A₃)-P(A₁)P(A₂)P(A₃)=

=0,1+0,2∙0,3-0,1∙0,2∙0,3=0,154

(при использовании теоремы умножения учли независимость событий А₁,А₂ и А₃).

Задача 3. Производительности трех станков, обрабатывающих одинаковые детали, относятся как 1:3:6. Из нерассортированной партии обработанных деталей взяты наудачу две. Какова вероятность того, что: а) одна из них обработана на 3-м станке; б) обе обработаны на одном станке?

Решение. а) Обозначим события:

A_i – деталь обработана на i-м станке (i=1,2,3);

В – одна из двух взятых деталей обработана на 3-м станке.

По условию P(A₁)==0,1, P(A₂)==0,3, P(A₃)= =0,6.

Очевидно, что В=А₁А₃+А₂А₃+А₃А₁+А₃А₂ (при этом надо учесть, что или первая деталь обработана на 3-м станке, или вторая). По теоремам сложения и умножения (для независимых событий)

P(B)=P(A₁)P(A₃)+P(A₂)P(A₃)+P(A₃)P(A₁)+P(A₃)P(A₂)=

=0,1∙0,6+0,3∙0,6+0,6∙0,1+0,6∙0,3=0,48.

б) Пусть событие С – обе детали обработаны на одном станке. Тогда С=А₁А₁+А₂А₂+А₃А₃ и

P(C)=0,1∙0,1+0,3∙0,3+0,6∙0,6=0,46.

Задача 4. Экзаменационный билет для письменного экзамена состоит из 10 вопросов – по 2 вопроса из 20 по каждой из пяти тем, представленных в билете. По каждой теме студент подготовил лишь половину всех вопросов. Какова вероятность того, что студент сдаст экзамен, если для этого необходимо ответить хотя бы на один вопрос по каждой из пяти тем в билете?

Решение. Обозначим события:

А₁,А₂ – студент подготовил 1-й, 2-й вопросы билета по каждой теме;

B_i – студент подготовил хотя бы один вопрос билета из двух по i-й теме (I=1,2,3,4,5);

С – студент сдал экзамен.

В силу условия С=В₁В₂В₃В₄В₅ . Полагая ответы студента по разным темам независимыми, по теореме умножения вероятностей

P(C)=P(B₁)P(B₂)P(B₃)P(B₄)P(B₅).

Так как вероятности P(B_i)(i=1,2,3,4,5) равны, то Р(С)=(Р(В_i))⁵.

P(B_i)=P(A₁+A₂)=1-P(₁₂)=

=1-P(₁)(₂)=1-=0,763.

Теперь Р(С)=0,763⁵=0,259.

Задача 5. При включении зажигания двигатель начнет работать с вероятностью 0,6. Найти вероятность того, что:

а) двигатель начнет работать при третьем включении зажигания;

б) для запуска двигателя придется включать зажигание не более трех раз.

Решение. а) Обозначим события:

А – двигатель начнет работать при каждом включении зажигания;

В – то же при третьем включении зажигания.

Очевидно, что В=А и Р(В)=Р()Р()Р(А)=0,4∙0,4∙0,6=

=0,096.

б) Пусть событие С – для запуска двигателя придется включать зажигание не более трех раз. Очевидно, событие С наступит, если двигатель начнет работать при 1-м включении, или при 2-м, или при третьем включении, т.е. С=А+А+А. Следовательно,

Р(С)=Р(А)+Р()∙Р(А)+ Р()∙Р()∙Р(А)=

=0,6+0,4∙0,6+0,4∙0,4∙0,6=0,936.

Задача 6. Вероятность попадания в мишень при каждом выстреле для 1-го стрелка равна 0,7, а для 2-го – 0,8. Оба они, начиная с 1-го, поочередно стреляют, но делают не более, чем по два выстрела, причем каждый стрелок стреляет второй раз только при условии, что при первом сделанном выстреле он промахнулся. Найти вероятность того, что в мишени ровно 2 пробоины.

Решение. Пусть события:

A_i ,B_i – попадание в цель соответственно 1-м и 2-м стрелком при i-м выстреле (i=1,2);

С – в мишени ровно 2 пробоины.

Событие C произойдет, если:

– у каждого стрелка по одному попаданию с первого раза;

– у 1-го стрелка – 2 попадания, у 2-го стрелка промах (при одном выстреле);

– у 1-го стрелка – промах и попадание, у 2-го стрелка – попадание (при одном выстреле);

– у 1-го стрелка 2 промаха, у 2-го стрелка – 2 попадания;

– у каждого стрелка – промах и попадание после двух выстрелов.

Итак,

C=A₁B₁+A₁₁A₂+₁B₁A₂+₁B₁₂B₂+₁₁A₂B₂.

Используя теоремы сложения для несовместных и умножения для независимых событий, получим

P(C)=P(A₁B₂+A₁₁A₂+₁B₁A₂+₁B₁₂B₂+₁₁A₂B₂)=

=0,7∙0,8+0,7∙0,2∙0,8+0,3∙0,8∙0,7+0,3∙0,8∙0,3∙0,8+

+0,3∙0,2∙0,7∙0,8=0,9312.

Задача 7. Среди билетов денежно-вещевой лотереи половина выигрышных. Сколько билетов нужно купить, чтобы с вероятностью, не меньшей 0,999, быть уверенным в выигрыше хотя бы по одному билету?

Решение. Пусть вероятность события A_i – выигрыша по i-му билету равна р, т.е. Р(А_i)=р. Тогда вероятность выигрыша хотя бы по одному из n приобретенных билетов, т.е. вероятность суммы независимых событий A₁,A₂ ,…,A_i ,…,A_n равна

P(A₁+A₂+…+A_n)=1-(1-p)ⁿ.

По условию 1-(1-p)ⁿ ≥ 0,999, откуда

(1-p)ⁿ ≤ 1-0,999.

Логарифмируя обе части неравенства, имеем

nlg(1-p) ≤ lg(0,001).

Учитывая, что lg(1-p) – величина отрицательная, получим

n ≥ [lg(0,001)]/lg(1-p)=9,96.

т.е. n ≥ 10 и необходимо купить не менее 10 лотерейных билетов.

Задачу можно решить, не прибегая к логарифмированию, путем подбора целого числа n, при котором выполняется неравенство (1-p)ⁿ ≤ 1-0,999, т.е. в данном случае ≤ 0,001; так, еще при n=9=>0,001, а уже приn=10=≤0,001, т.е. n≥10.

Задача 8. Два игрока поочередно бросают игральную кость. Выигрывает тот, у которого первым выпадет «6 очков». Какова вероятность выигрыша для игрока, бросающего кость первым? Вторым?

Решение. Обозначим события:

A_i – выпадение 6 очков при i-м бросании игральной кости (i=1,2,...);

В – выигрыш игры игроком, бросающим кость первым.

Имеем P(A_i)=1/6, P(_i)=5/6 при любом i.

Событие В можно представить в виде суммы вариантов:

B=A₁+₁₂A₃+_{123 4} A₅+... Поэтому

P(B)=P(A₁)+P(₁₂A₃)+P(_{123 4} A₅)+...=

+∙+∙+...

По формуле суммы геометрического ряда с первым членом а=1/6 и знаменателем q=(5/6)²<1

P(B)== ==0,545.

Вероятность P() выигрыша игры игроком, бросающим игральную кость вторым, равна

P()=1-P(B)=1-6/11=5/11=0,455,

т.е. существенно меньше, чем игроком, бросающим игральную кость первым.

Домашнее задание.

Задача 1. На полке находится 10 книг, расставленных в произвольном порядке. Из них три книги по теории вероятностей, три – по математическому анализу и четыре – по линейной алгебре. Студент случайным образом достает одну книгу. Какова вероятность того, что он возьмет книгу по теории вероятностей или по линейной алгебре?

P=0,7.

Задача 2. Магазин получил продукцию в ящиках с четырех оптовых складов: четыре с первого, пять со второго, семь с третьего и четыре с четвертого. Случайным образом выбран ящик для продажи. Какова вероятность того, что это будет ящик с первого или третьего склада?

Задача 3. В порт приходят корабли только из трех пунктов отправления. Вероятность появления корабля из первого пункта равна 0,2, из второго пункта – 0,6. Найти вероятность прибытия корабля из третьего пункта.

Задача 4. Вероятность правильного оформления счета на предприятии составляет 0,95. Во время аудиторской проверки были взяты два счета. Какова вероятность того, что только один из них оформлен правильно?

Задача 5. Вероятность правильного оформления накладной при передаче продукции равна 0,8. Найти вероятность того, что из трех накладных только две оформлены правильно.

Задача 6. В районе 100 поселков. В пяти из них находятся пункты проката сельхозтехники. Случайным образом отобраны два поселка. Какова вероятность того, что в них окажутся пункты проката?

P=.

Задача 7. В городе находятся 15 продовольственных и 5 непродовольственных магазинов. Случайным образом для приватизации были отобраны три магазина. Найти вероятность того, что все эти магазины непродовольственные.

Задача 8. В магазине имеются 10 женских и 6 мужских шуб. Для анализа качества были отобраны три шубы случайным образом. Определить вероятность того, что среди отобранных шуб окажутся:

а) только женские шубы;

б) только мужские или только женские шубы.

Задача 9. На предприятие поступают заявки от нескольких торговых пунктов. Вероятности поступления заявок от пунктов А и В равны соответственно 0,5 и 0,4. Найти вероятность поступления заявок от пункта А или от пункта В, считая события поступления заявок от этих пунктов независимыми, но совместными.

Задача 10. Предприятие обеспечивает регулярный выпуск продукции при безотказной поставке комплектующих от двух смежников. Вероятность отказа в поставке продукции от первого из смежников равна 0,05, от второго – 0,08. Найти вероятность сбоя в работе предприятия.

СМОЛЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Г. С. ЕВДОКИМОВА

ПРАКТИКУМ

ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКОЙ

СТАТИСТИКЕ

МОДУЛЬ 3

Формула полной вероятности

и формула Байеса.

Смоленск 2009

Если некоторое событие А совершается с одним из n несовместных событий (гипотез) H₁, H₂,…, H_n, образующих полною группу событий, то для определения вероятности этого события может быть использована формула полной вероятности

Для определения вероятности события H_i, при условии, что произошло событие А, используется формула Байеса

Цель занятия: Научить студентов правильно пользоваться формулами полной вероятности и Байеса.

При решении задач на формулу полной вероятности следует нацеливать студентов на то, чтобы они после введения обозначений и соответствующих рассуждений приходили к записи типа а затем уже производили вычисления вероятностей.

При этом студент должен знать, что формула полной вероятности применяется при рассмотрении событий до опыта, т.е. в условии задачи не должно быть результата проведенного опыта. Формула Байеса применяется, когда в результате проведённого опыта некоторое событие осуществляется и требуется найти условные вероятности для каждой из гипотез. Успешность решения задачи, как будет показано ниже, определяет умение правильно выбрать гипотезы.

К занятию по данной теме должны быть подготовлены ответы на следующие вопросы:

1) Как называется в формуле полной вероятности вероятности гипотез P(H_i)?

2) Как называются в формуле полной вероятности вероятности P(A/H_i)?

3) Вероятности каких событий находятся по формуле Байеса?

4) В чём суть байесовского подхода при научных исследованиях?

Задача 1. Партия транзисторов, среди которых 10% дефектных, поступила на проверку. Схема проверки такая, что с вероятностью 0,95 обнаруживается дефект и существует вероятность 0,03 того, что исправный транзистор будет признан дефектным. Какова вероятность того, что случайно выбранный из партии транзистор будет признан дефектным?

Решение. Обозначим через А событие, состоящее в том, что выбранный транзистор будет признан дефектным. Событие А может произойти двумя способами — поступивший на проверку транзистор дефектный (событие H₁) и дефект будет обнаружен или поступивший на проверку транзистор исправный (событие H₂) и он ошибочно будет признан дефектным. Последнюю фразу можно символически записать . Поэтому искомую вероятность находим по формуле полной вероятности

Задача 2. Имеются три одинаковые с виду урны. В первой 3 белых и 4 черных шара, во второй 2 белых и 3 черных шара, а в третьей - только белые шары. Из взятой наугад урны вынимаем один шар. Какова вероятность того, что это будет белый шар?

Решение. Обозначим через А событие, состоящее в извлечении белого шара. Извлечение белого шара может произойти следующим образом. Выбирается первая урна (событие H₁) и из нее вынимается белый шар или выбирается вторая урна (событие H₂) и из нее вынимается белый шар, или выбирается третья урна (событие H₃) и из нее вынимается белый шар. Символически это можно записать . В силу несовместности и зависимости событий приходим к формуле полной вероятности.

P (А) = Р(H₁) Р (А/ H₁) + Р (H₂) Р (А/ H₂) + Р (H₃) Р (А/ H₃),

вычисления по которой дают

Задача 3. В торговую фирму поступили телевизоры от трёх поставщиков в отношении 1:4:5. Практика показала, что телевизоры, поступающие от 1-го, 2-го и 3-го поставщиков, не потребуют ремонта в течение гарантийного срока соответственно в 98%, 88 и 92% случаев.

1) Найти вероятность того, что поступивший в торговую точку телевизор не потребует ремонта в течение гарантийного срока. 2) Проданный телевизор потребовал ремонта в течение гарантийного срока. От какого поставщика вероятнее всего поступит этот телевизор?

Решение. 1) Обозначим события:

H_i – телевизор поступил в торговую фирму от i-го поставщика (i=1,2,3);

A – телевизор не потребует ремонта в течении гарантийного срока.

По условию

По формуле полной вероятности

2) Событие - телевизор потребует ремонта в течение гарантийного срока;

По условию

По формуле Байеса

Таким образом после наступления события вероятность гипотезыН₂ увеличилась с Р(Н₂)=0,4 до максимальной а гипотезы Н₃ – уменьшилась от максимальной Р(Н₃) = 0,5 до если ранее (до наступления событияА) наиболее вероятной была гипотеза Н₃, то теперь, в свете новой информации (наступления события А), наиболее вероятна гипотеза Н₂ – поступления данного телевизора от 2-го поставщика.

Задача 4. Два стрелка независимо друг от друга стреляют по мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8; для второго – 0,4. После стрельбы в мишень обнаружена одна пробоина. Какова вероятность того, что она принадлежит: а) 1-му стрелку; б) 2-му стрелку?

Решение. Обозначим события:

Н₁ – оба стрелка не попали в мишень;

Н₂ – оба стрелка попали в мишень;

Н₃ – 1-й стрелок попал в мишень, 2-й нет;

Н₄ – 1-й стрелок не попал в мишень, 2-й попал;

А – в мишени одна пробоина (одно попадание).

Найдём вероятности гипотез и условные вероятности события А для этих гипотез:

Теперь по формуле Байеса

т.е. вероятность того, что попал в цель 1-й стрелок при наличии одной пробоины, в 6 раз выше, чем для второго стрелка.

Задача 5. В среднем из каждых 100 клиентов отделения банка 60 обслуживаются первым операционистом и 40 – вторым операционистом. Вероятность того, что клиент будет обслужен без помощи заведующего отделением, только самим операционистом, составляет 0,9 и 0,75 соответственно для первого и второго служащих банка. Найти вероятность полного обслуживания клиента первым операционистом.

Решение. Вероятность того, что клиент попадёт к первому операционисту (событие Н₁), составляет 0,6, ко второму – 0,4 (событие Н₂). Искомая вероятность полного обслуживания клиента первым операционистом (событие А) определяется по формуле Байеса:

Иными словами, 64% клиентов, попавших на обслуживание к первому операционисту, будут обслужены им полностью.

Дополнительные задачи.

Задача 1. Из полной колоды в 52 карты на удачу последовательно и без возвращения выбирают две карты. Какова вероятность того, что второй картой можно покрыть первую? (Это значит, что вторая карта должна быть более старшей картой той же масти).

Решение. Пусть А - интересующее нас событие. В качестве первой попытки выберем следующие гипотезы: H = {в составе двух вынутых карт равно k картинок}, k = 0, 1, 2, (к картинкам относятся валет, дама, король и туз каждой масти).

Ясно, что {H} (k = 0, 1, 2) – разбиение множества , так как выполнены все три условия, сформулированные в определение разбиения множества (проверьте!). Кроме того, нетрудно вычислить безусловные вероятности гипотез Р (Н).

Однако вычисление условных вероятностей Р (А/Н) оказывается делом не менее трудным, чем ответ на первоначально поставленный вопрос о вероятности события Р(А). Это объясняется тем ,что связь события А с данными гипотезами Н не может быть достаточно просто описана на языке алгебраических операций.

Рассмотрим более удачный для решения задачи вариант разбиения {Н} (k = 2, 3, … ,14), где Н = {первая вытянутая карта оценивается в k очков}, при этом значению k = 2 соответствует двойка, k = 3 – тройка, …, k = 11 – валет, k = 12 – дама, k = 13 – король и k = 14 – туз. Вычислим условные вероятности, применяя метод вспомогательного эксперимента. Р(А/Н) = Р{вторая вытянутая карта той же масти, причем ее достоинство оценивается не ниже, чем в k +1 очко} = (14 - k ) / 51 в силу формулы классической вероятности. Безусловные вероятности гипотез Р(Н) = 1 / 13 в силу равновероятности событий Н = {вытянуть карту произвольной масти, оцениваемую в k очков}. Применяя формулу полной вероятности, получим

Р(А) =.

Еще более простой путь решения получается, если ввести следующее разбиение множества  в данном эксперименте: {Н} (k = 1, 2), где H = {обе вынутые карты одной масти}, Н= {две карты разной}. Очевидно, чтоР(А/Н) = 0, поэтому вторая гипотеза исключается из формулы полной вероятности и Р(Н) = 12 / 51 = 4 / 17 (первая карта может быть произвольной масти, вторая должна быть той же масти, что и первая). Пусть теперь выполнено событие Н, т.е. обе карты одной масти. Тогда та из них, которую извлекли второй по счету, должна быть старше первой. Но в силу равновероятности исходов = {вторая карта старше первой} и ₂= {первая карта старше второй} в этом вспомогательном эксперименте получаем Р(А/Н₁) = =0,5, поэтому

Задача 2. В условиях эксперимента, описанного в задаче 1, случайно выбранный из партии транзистор был признан дефектным. Какова вероятность того, что на самом деле транзистор исправен?

Решение. В обозначениях задачи 1 требуется вычислить Р(Н/А) (апостериорную условную вероятность гипотезы Н).

По формуле Байеса

.

Таким образом, апостериорная условная вероятность того, транзистор на самом деле исправный, если известно, что он был признан дефектным, существенно меньше априорной вероятности гипотезы Н, что явилось следствием поступившей информации.

Особое значение приобретает формула Байеса для таких экспериментов, в которых гипотезы Ннепосредственно не наблюдаемы, хотя априорные вероятности Р(Н) и соответствующие условные вероятности Р(А/Н),k = 1,…, n, известны из дополнительных опытов. Такая ситуация может иметь место, например, если отсутствует прибор, позволяющий регистрировать факт осуществления данных гипотез, или же если применение прибора для регистрации осуществления гипотез приводит к разрушению предмета наблюдения (разрушающий контроль). Для подобных экспериментов переоценка вероятностей гипотез после опыта может быть проведена на основании наблюдаемого события А, тесно связанного с гипотезами. Такой подход часто используется в задачах медицинской и технической диагностики.

Задача 3. Изучается три вида дефектов запоминающих устройств, выполненных на интегральных схемах: дефекты схем обрамления (гипотеза Н, Р(Н) = 0,1), дефекты вызванные паразитными связями между ячейками (гипотеза Н, Р(Н)= =0,6)и дефекты адресных шин (гипотеза Н, Р(Н) = 0,3). Диагностика запоминающих устройств производится с помощью набора тестов Т, Т ,…, Т, каждый из которых проверяет определенное состояние ячейки памяти. Наблюдаемый результат – состояние выбранной ячейки по отношению к каждому тесту. Пусть диагностика произведена и наблюдался некоторый результат (произошло событие А). Известно до опыта, что

Р(А / Н ) = 0,4 , Р(А / Н) = 0,2 , Р(А / Н) = 0,3.

Установить, какая из гипотез имеет наибольшую апостериорную вероятность (т.е. какой из дефектов наиболее вероятен).

Решение. Вычислим сначала полную вероятность осуществления события А. Используя данные задачи и применяя формулу полной вероятности, получим

Р(А) =.

Для ответа на вопрос, какой из дефектов имеет наибольшую апостериорную вероятность, заметим, что в числителе формулы Байеса стоит слагаемое полной вероятности, относящееся к данной переоцениваемой гипотезе. Сравнивая эти слагаемые для трех заданных гипотез, получаем, что наибольшую вероятность имеет гипотеза Н: Р(Н/А) = 0,12 / 0,25 = 0,48.

Домашнее задание.

Задача 1. На автозавод поступили двигатели от трёх моторных заводов. От первого завода поступило 10 двигателей, от второго – 6 и от третьего – 4 двигателя. Вероятность безотказной работы этих двигателей в течение гарантийного срока соответственно равны 0,9; 0,8; 0,7.

Какова вероятность того, что:

а) установленный на машине двигатель будет работать без дефектов в течение гарантийного срока;

б) проработавший без дефекта двигатель изготовлен на первом заводе, на втором заводе?

Задача 2. На предприятии, изготавливающем замки, первый цех производит 25, второй 35, третий 40% всех замков. Брак составляет соответственно 5, 4 и 2%.

а) Найти вероятность того, что случайно выбранный замок является дефектным.

б) Случайно выбранный замок является дефектным. Какова вероятность того, что он был изготовлен в первом, втором, третьем цехе?

Задача 3. Трое рабочих изготавливают однотипные изделия. Первый рабочий изготовил 40 изделий, второй – 35, третий – 25. Вероятность брака у первого рабочего 0,03, у второго – 0,02, у третьего – 0,01. Взятое наугад изделие оказалось бракованным. Определить вероятность того, что это изделие сделал второй рабочий.

Задача 4. На предприятии работают две бригады рабочих: первая производит в среднем ¾ продукции с процентом брака 4%, вторая – ¼ продукции с процентом брака 6%. Найти вероятность того, что взятое наугад изделие:

а) окажется бракованным;

б) изготовлено второй бригадой при условии, что изделие оказалось бракованным.

Задача 5. В обувную мастерскую для ремонта приносят сапоги и туфли в соотношении 2:3. Вероятность качественного ремонта для сапог равна 0,9, а для туфель – 0,85. Проведена проверка качества одной пары обуви. Оказалось что эта пара обуви отремонтирована качественно. Какова вероятность того, что это а) сапоги, б) туфли?

Ответы: 1) а) Р(А) = 0,83; б) Р(Н₁/А) = 0,54; Р(Н₂/А) = = 0,29. 2) а) Р(А) = 0,0345; б) Р(Н₁) = 0,362; Р(Н₂) = 0,408; Р(Н₃) = 0,232. 3) Р(А) = 0,326. 4) а) Р(А) = 0,045; б) Р(А) = = 0,33. 5) а) Р(А) = 0,41; б) Р(А) = 0,59.

СМОЛЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Г. С. ЕВДОКИМОВА

ПРАКТИКУМ

ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКОЙ

СТАТИСТИКЕ

МОДУЛЬ 4

Схема независимых испытаний. Простейший поток событий

Смоленск 2009

Если при проведении испытаний вероятность события Ане зависит от исходов других испытаний, то такие события называются независимыми.

Формула Бернулли определяет вероятность появления ровно m раз события A в серии из n независимых испытаний, в каждом из которых вероятность появления события A равна p:

P_n(m)=p^mq^n-m,

где =, q=1-p.

При больших n и маленьких p вычисления по формуле Бернулли затруднены. В этих случаях используется формула Пуасона

P_n(m)≈e^{- λ}, λ=n∙p.

Цель занятия: 1. Научить студентов в конкретных ситуациях распознавать схему независимых испытаний и научить подбирать соответствующую формулу для вычисления вероятностей:

n-мало формула Бернулли

P_n(k) формула Лапласа

n-велико

p<0,1 формула Пуассона,

хотя формула Лапласа на данном занятии и не используется.

2. Закрепить в сознании студента понятие простейшего потока событий. При решении задач обратить внимание студентов на то, что Полезно обратить внимание студентов и на многообразное содержание, которое может быть вложено в схему независимых испытаний. При решении задач №5 и №6 подробно обсудить условия (отсутствие последствия, ординарность), определяющие простейший поток событий.

Задача 1. Каждый пятый клиент банка приходит брать проценты со вклада. Сейчас в банке ожидают своей очереди обслуживания шесть человек. Найти вероятность того, что из них будут брать проценты: а) только два человека; б) хотя бы один.

Решение. В задаче реализуется схема испытаний Бернулли. Здесь A – «человек в очереди будет брать проценты», тогда вероятность «успеха» p=1/5, а вероятность «неудачи» q=4/5.

а) P₆(2)==,

б) P₆(m≥1)=1-P₆(0)=1-≈.

Задача 2. На каждый вопрос предлагается три ответа, среди которых следует выбрать правильный. Задано пять вопросов. Какова вероятность того, что путем простого угадывания удастся правильно ответить на четыре вопроса? Какова вероятность правильно ответить хотя бы на один вопрос?

Решение. Выбор ответа на каждый вопрос можно рассматривать как независимое испытание, вероятность «успеха» в котором p = 1/3. Тогда вероятность правильно ответа на четыре вопроса равна

вероятность угадать ответ хотя бы на один вопрос равна

Задача 3. В среднем 20% пакетов акций на аукционах продаются по первоначально заявленной цене. Найти вероятность того, что из 9 пакетов акций в результате торгов по первоначально заявленной цене: 1) не будут проданы 5 пакетов; 2) будет продано а) не менее 2 пакетов; б) не более 2; в) хотя бы 2 пакета.

Решение. 1) Вероятность того, что пакет акций не будет продан по первоначально заявленной цене, p=1-0,2=0,8.

По формуле Бернулли

P_5,9=∙0,8⁵∙0,2⁴=0,066.

2.а) По условию p=0,2.

P₉(m<2)=P_0,9+P_1,9=∙0,2⁰∙0,8⁹+∙0,2∙0,8⁸=0,436.

2.б) P₉(m≤2)=P_0,9+P_1,9+P_2,9=∙0,2⁰∙0,8⁹+∙0,2∙0,8⁸+∙0,2²∙0,8⁷==0,738.

2.в) P₉(m≥2)=P_2,9+P_3,9+...+P_9,9.

Указанную вероятность можно найти проще, если перейти к противоположному событию, т.е.

P₉(m≥2)=1-P₉(m<2)=1-(P_0,9+P_1,9)=1-0,436=0,564.

Задача 4. Вероятность попадания торпеды в корабль равна 0,3. Сколько можно выпустить торпед, чтобы вероятность поражения цели была больше 0,9.

Решение. На языке схемы испытаний Бернулли за «успех» считаем попадание торпеды в корабль, за «неудачу» — промах, тогда вероятность «успеха» p = 0,3, а «неудачи» — q = 0,7. Цель будет поражена, если в n выстрелах будет хотя бы одно попадание, т. е.

Задача 5. Вероятность того, что изделие при транспортировке повредится равна 0,0005. С завода отправлено четыре тысячи изделий. Найти вероятность того, что в пути повредится больше двух изделий.

Решение. Так как n велико, а p мало, то удобно пользоваться формулой Пуассона, p = 0,0005,

Нас интересует вероятность

Р₄₀₀₀(m > 2) = P₄₀₀₀ (3) +…+P₄₀₀₀(4000).

Проще вычислить эту вероятность, если рассмотреть противоположное событие:

Задача 6. В течение часа на коммутатор поступает в среднем 120 телефонных вызовов. Какова вероятность того, что в течение заданной минуты поступит четыре вызова?

Решение. Телефонные вызовы поступают независимо друг от друга и по одному, т.е. выполняется условия простейшего потока событий. Значит, все вероятности определяются средним числом событий.В нашем случае на интервал времениt=Iмин. приходится в среднем ==2 вызова. Поэтому по формуле Пуассона: Р(4)=е.

Задача 7. Известно, что наборщик в среднем допускает одну ошибку на две страницы текста. В набранной книге взяли наугад страницу. Какова вероятность того, что на ней нет опечаток? Какова вероятность того, что на ней больше одной опечатки?

Решение. Опечатки появляются независимо друг от друга и по одной. Условия простейшего потока приблизительно выполняются и формула Пуассона приблизительно верна. На одну страницу приходится в среднем =опечатки. Поэтому

Р(0)=е0,6.Р(m>1)=1–Р(0)–Р(1)=1–0,6–0,3=0,1.

Задача 8. На факультете насчитывается 500 студентов. Какова вероятность того, что 1 сентября является днем рождения одновременно для m студентов данного факультета? Вычислить указанную вероятность для значений m = 0, 1, 2, 3.

Решение. Так как n = 500 >1 и р = Р {родится 1 сентября любому из студентов факультета} = 1/365 < 1, то можно использовать формулу Пуассона с параметром  = 1,36986. Находим

P₅₀₀(0)= e^{- λ} ≈ 0,2541,

P₅₀₀(1)= ≈ 0,3481,

P₅₀₀(2)= ≈ 0,2385,

P₅₀₀(3)= ≈ 0,1089.

Значения искомых вероятностей, соответствующих биноминальному распределению В(500, 1/365) и вычисленных с 4 верными знаками после запятой, таковы:

P₅₀₀(0) = 0,2537, P₅₀₀ (1) = 0,3485, P₅₀₀(2) = 0,2389, P₅₀₀(3)= =0,1089.

Дополнительные задачи.

Задача 1. Вероятность малому предприятию быть банкротом за время t равна 0,2. Найти вероятность того, что из восьми малых предприятий за время t сохранятся: а) два; б) не более двух.

Ответ: а) P_2,6=p²q⁴=0,717; б) P₆(m>2)=1-P₆(m<2)=

=1-(P_0,6+P_1,6)=0,999.

Задача 2. Предполагается, что 10% открывающихся вновь малых предприятий прекращает свою деятельность в течение года. Какова вероятность того, что из шести малых предприятий не более двух в течение года прекратят свою деятельность?

Ответ: P₆(m≤2)=P_0,6+P_1,6+P_2,6=0,984.

Задача 3. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье: а) не менее трех мальчиков; б) не более трех мальчиков.

Ответ: а) P₁₀(m≥3)=1-P₁₀(m<3)=1-(P_0,10+P_1,10+P_2,10)=0,945; б) P₁₀(m≤3)=P_0,10+P_1,10+P_2,10+P_3,10=0,172.

Задача 4. Два равносильных противника играют в шахматы. Что более вероятно: а) выиграть 2 партии из 4 или 3 партии из 6?; б) не менее 2 партий из 4 или не менее 3 партий из 6? (Ничьи в расчет не принимаются).

Ответ: а) 2 партии из 4, ибо P_2,4=p²q²=0,375, а P_3,6=p³q³=0,312; б) не менее 2 партий из 4, ибо P₄(m≥2)=P_2,4+P_3,4+P_4,4=0,688, а P₆(m≥3)=1-P₆(m<3)=1-(P_0,6 + +P_1,6+P_2,6)=0,656.

Задача 5. В банк отправлено 4000 пакетов денежных знаков. Вероятность того, что пакет содержит недостаточное или избыточное число денежных знаков, равна 0,0001. Найти вероятность того, что при проверке будет обнаружено: а) три ошибочно укомплектованных пакета; б) не более трех пакетов.

Ответ: а) P_3,4000=P₃(0,4)=0,00715; б) P₄₀₀₀(m≤3)=P_0,4000+ +P_1,4000+P_2,4000+P_3,4000=0,9992.

Домашнее задание.

Задача 1. Четыре покупателя приехали на оптовый склад. Вероятность того, что каждому из этих покупателей потребуется холодильник марки «А», равна 0,4. Найти вероятность того, что холодильник потребуется:

а) не менее, чем двум покупателям;

б) не более, чем трем покупателям;

в) всем четырем покупателям.

Задача 2. Работают четыре магазина по продаже стиральных машин. Вероятность отказа покупателю в магазинах равна 0,1. Считая, что ассортимент товара в каждом магазине формируется независимо от других, определить вероятность того, что покупатель получит отказ в двух, в трех и в четырех магазинах.

Задача 3. Обувной магазин продал 200 пар обуви. Вероятность того, что в магазин будет возвращена бракованная пара равна 0,01. Найти вероятность того, что из проданных пар обуви будет возвращено а) ровно 4 пары, б) ровно 5 пар.

Задача 4. В новом микрорайоне поставлено 10 000 кодовых замков на входных дверях домов. Вероятность выхода из строя одного замка в течение месяца равна а) 0,0002; б) 0,001. Найти вероятность того, что за месяц откажут два, три и пять замков.

Задача 5. На станциях отправления поездов находится 1000 автоматов для продажи билетов. Вероятность выхода из строя одного автомата в течение часа равна 0,004. Какова вероятность того, что в течение часа из строя выйдут два, три и пять автоматов?

Ответы: 1) а) P(X≥2)=0,5248; б) P(X≤3)=0,9744; в) P(X=4)=0,0256. 2) P₄(2)=0,0486; P₄(3)=0,0036;P₄(4)=0,0001. 3) а) P₂₀₀(4)=0,09; б) P₂₀₀(5)=0,036. 4) б) P₁₀₀₀₀(2)=0,00225; P₁₀₀₀₀(3)=0,0075; P₁₀₀₀₀(5)=0,0375; 5) P₁₀₀₀(2)=0,1464; P₁₀₀₀(3)=0,1952; P₁₀₀₀(5)=0,1562.

СМОЛЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Г. С. ЕВДОКИМОВА

ПРАКТИКУМ

ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

И МАТЕМАТИЧЕСКОЙ

СТАТИСТИКЕ

МОДУЛЬ 5