Практическое занятие №4

Механические колебания и волны.

Цель работы: научиться рассчитывать параметры колебаний (амплитуду, фазу, циклическую частоту, частоту, период), научиться применять уравнение гармонических колебаний, научиться рассчитывать колебания математического и пружинного маятника.

Приборы и оборудование: линейка, карандаш, задание.

1. Краткие теоретические сведения

Колебания – явления или процессы, имеющие ту или иную степень повторяемости во времени.

Параметры, описывающие колебательное движение:

1. Период (Т) – время одного полного колебания (измеряется в секундах).

2. Частота (v) – физическая величина, показывающая, сколько полных колебаний система совершает в единицу времени (измеряется в Гц (1 Гц = с^–1)).

3. Циклическая частота колебаний ( ) – физическая величина, показывающая, сколько полных колебаний система совершает за 2 секунд (измеряется в Гц).

4. Амплитуда (x_m или S_m) – максимальное отклонение системы от положения равновесия (измеряется в метрах).

5. Мгновенное значение отклонения системы от положения равновесия (х или S) – отклонение системы от положения равновесия в данный момент времени (измеряется в метрах).

Зависимости между параметрами:

; .

Гармонические колебания – колебания, происходящие по закону синуса или косинуса.

Математический маятник – материальная точка, подвешенная на невесомой и нерастяжимой нити.

Колебания математического маятника будут гармоническими при малых углах отклонения от положения равновесия (или при условии, что амплитуда колебаний гораздо меньше длины подвеса маятника).

Формулы для расчета частоты ( ) и периода (Т) свободных колебаний математического маятника:

; .

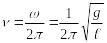Период свободных колебаний математического маятника не зависит от: 1) массы подвешенной материальной точки; 2) амплитуды (изохронность колебаний).

Пружинный маятник – тело, скрепленное с пружиной.

Колебания пружинного маятника будут гармоническими при условии, что амплитуда колебаний лежит в пределах выполнения закона Гука.

Формулы для расчета частоты ( ) и периода (Т) колебаний пружинного маятника:

; .

Период колебаний пружинного маятника зависит от: 1) массы скрепленного с пружиной тела; 2) жесткости пружины.

Превращения механической энергии при колебаниях математического и пружинного маятников: 1) каждые четверть периода потенциальная энергия превращается в кинетическую и обратно; 2) в любой момент времени сумма потенциальной и кинетической энергий маятника (полная энергия колебаний) неизменна.

Методические рекомендации к решению задач по теме «Законы сохранения импульса и механической энергии»

Гармонические колебания происходят по синусоидальному или косинусоидальному закону:

х = х_mcos(ωt + φ_o) = х_mcos( + φ_o) = х_mcos(2πνt + φ_o),

где х_m – амплитуда колебаний, ω – циклическая частота колебаний, ν – частота колебаний, Т – период колебаний.

Для определения частоты гармонических колебаний можно использовать разные приёмы:

1. использовать связь возвращающей силы со смещением, а циклическую частоту определить через коэффициент k возвращающей силы по формуле ;

2. использовать закон сохранения полной механической энергии и полученное выражение продифференцировать по времени (в результате получается дифференциальное уравнение гармонических колебаний);

3. сравнить колебания данного тела (колебательной системы) с колебаниями математического маятника, имеющего ту же частоту и период (применяется к системам, совершающим колебания вокруг оси, совпадающей с точкой подвеса).

При первом способе необходимо:

1. сделать схематический чертёж, на котором изобразить исследуемое тело в положении равновесия;

2.указать действующие на тело силы и написать уравнение равновесия в проекциях на координатную ось, направленную вдоль возможных колебаний тела;

3. мысленно сместить тело из положения равновесия на х и отпустить;

4. выяснить, какие силы изменились по модулю, а какие остались неизменными;

5. написать уравнение движения тела для какого-либо промежуточного положения (не равновесия и не в крайних точках) на траектории в виде max = , где – сумма проекций на координатную ось всех действующих на тело сил.

Учесть при этом:

а) противоположные знаки проекций на координатную ось смещения тела вдоль координатной оси и равнодействующей сил;

б) учесть условие равновесия тела (при этом некоторые слагаемые в уравнении движения тела уничтожатся).

6. Привести уравнение движения тела к виду циклическая частота колебаний тела.

7. Определить частоту свободных колебаний тела и период по формулам:

.

При втором способе необходимо:

1. выполнить пункты 1 – 4, записанные для первого способа;

2. если положение тела в поле силы тяжести изменяется, то нужно выбрать уровень с нулевой потенциальной энергией в этом поле;

3. написать выражения для расчёта полной механической энергии тела в начальном Е₁ и промежуточном Е₂ положении;

4. приравнять эти выражения;

5. взять от обеих частей полученного равенства производную по времени. При этом учесть, что:

а)

б) .

6. получить в результате дифференциальное уравнение гармонических колебаний:

или , где х – смещение тела из положения равновесия, α – угол отклонения нити, к которой прикреплено тело, или любого подвеса от вертикали.

При действиях по третьему способу необходимо:

1. определить положение центра масс (центра тяжести) системы;

2. выбрать нулевой уровень отсчёта потенциальной энергии системы в поле силы тяжести (удобно связать его с положением равновесия);

3. мысленно отклонить систему от положения равновесия на малый угол α;

4. написать выражение для расчёта потенциальной энергии системы в поле силы тяжести при отклонении от положения равновесия;

5. написать выражение для расчёта кинетической энергии системы тел при возвращении системы в положение равновесия. При этом учесть, что υ = ωR – линейная скорость на расстоянии R от точки подвеса (угловая скорость всех тел системы одинакова);

6. приравнять выражения для расчёта потенциальной и кинетической энергии системы и получить формулу для α²;

7. провести вычисления, указанные в пунктах 1 – 6, для математического маятника некоторой длины ℓ, колеблющегося с такой же частотой при отклонении на такой же малый угол α;

8. приравнять два выражения для α² и получить значение ℓ;