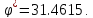6 Оглавление

Исходные данные 5

Задание №1. Графоаналитическое решение ОЗЛП 6

Задание № 2. Задача о коммивояжере. Метод ветвей и границ 11

Задание №3. Оптимизация дискретных управлений дискретными динамическими объектами методом динамического программирования Р. Беллмана 20

Задание №4. Синтез непрерывного оптимального управления с помощью уравнения Эйлера 24

Задание №5. Синтез непрерывных оптимальных уравнений с помощью уравнения Эйлера-Пуассона 29

Исходные данные

К заданию №1.

№	C1	C2	B1	B2	B3	B4	A11	A12	A21	A22	A31	A32	A41	A42
217	2,5	3,5	12	5	2	2	-1	8	2	-1,5	-2	2	1	-2

К заданию №2.

		1	2	3	4	5	6
С =	1	∞	4	5	6	7	1
	2	1	∞	1	3	2	4
	3	6	5	∞	1	4	3
	4	1	7	6	∞	5	1
	5	4	1	2	5	∞	4
	6	5	6	3	4	1	∞

К заданию №3.

№	A	B	α	β	γ
117	1	0,5	4	2	8

К заданию №4.

№	A	B	α2
117	1,4	0,7	12

К заданию №5.

№	k	γ
117	34	17

Задание №1. Графоаналитическое решение озлп

1. Математическая постановка ОЗЛП:

φ=2,5x₁+3,5x₂→max, (0)

-x₁+8x₂≤12, (1)

x₁-1,5x₂≤5, (2)

-2x₁+2x₂≤2, (3)

x₁-2x₂≤2, (4)

x₁≥0, (5)

x₂≥0, (6)

CE: -x₁+8x₂=12, (1’)

x₁-1,5x₂=5, (2’)

BC: -2x₁+2x₂=2, (3’)

DE: x₁-2x₂=2, (4’)

AD:x₁=0, (5’)

AB:x₂=0, (6’)

2. Записываем уравнение граничных линий допустимого многоугольника (1’) -(6’).

Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

Построим уравнение -x₁+8x₂= 12 по двум точкам. Для нахождения первой точки приравниваем x₁= 0. Находим x₂= 1.5. Для нахождения второй точки приравниваем x₂= 0. Находим x₁= -12. Соединяем точку (0;1.5) с (-12;0) прямой линией.

Построим уравнение x₁-1.5x₂= 5 по двум точкам. Для нахождения первой точки приравниваем x₁= 0. Находим x₂= -3.33. Для нахождения второй точки приравниваем x₂= 0. Находим x₁= 5. Соединяем точку (0;-3.33) с (5;0) прямой линией.

Построим уравнение -2x₁+2x₂= 2 по двум точкам. Для нахождения первой точки приравниваем x₁= 0. Находим x₂= 1. Для нахождения второй точки приравниваем x₂= 0. Находим x₁= -1. Соединяем точку (0;1) с (-1;0) прямой линией.

Построим уравнение x₁-2x₂= 2 по двум точкам. Для нахождения первой точки приравниваем x₁= 0. Находим x₂= -1. Для нахождения второй точки приравниваем x₂= 0. Находим x₁= 2. Соединяем точку (0;-1) с (2;0) прямой линией.

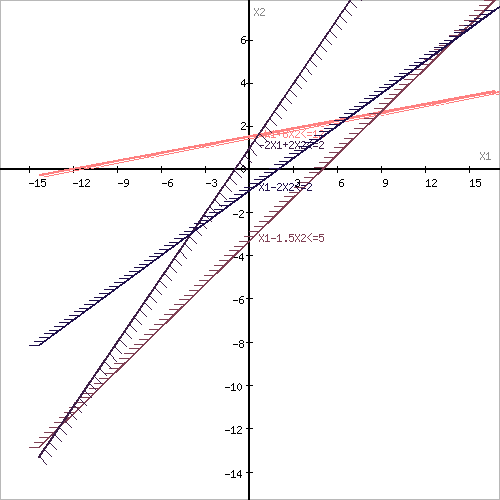
3. Строим линию, пересекающую область φ.

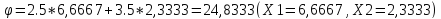, (7)

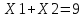, (8)

4. Находим градиент целевой функции:

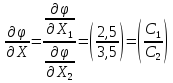, (9)

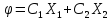, (10)

Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.

Обозначим границы области многоугольника решений.

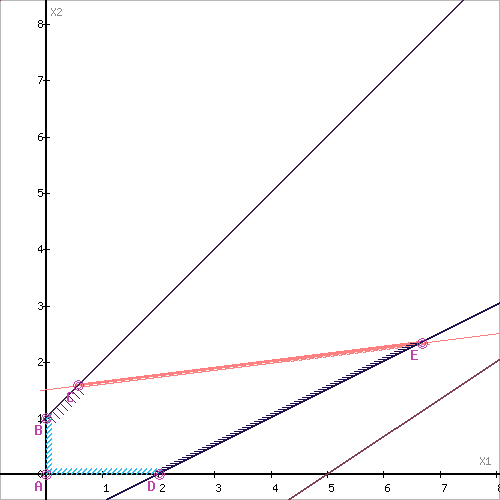
Рассмотрим целевую функцию задачи F = 2.5x1+3.5x2 → max. Построим прямую, отвечающую значению функции F = 0: F = 2.5x1+3.5x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (2.5; 3.5). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.

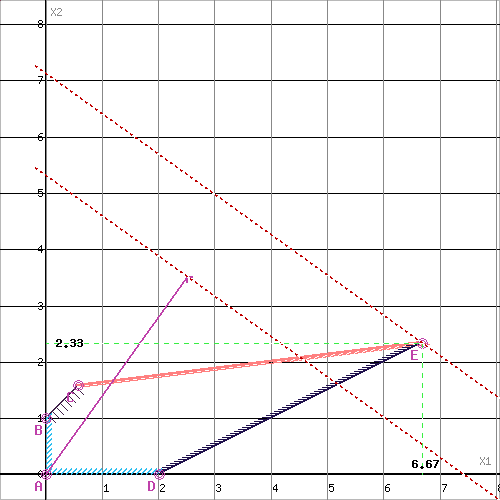
Прямая F(x) = const пересекает область в точке E. Так как точка E получена в результате пересечения прямых (1) и (4), то ее координаты удовлетворяют уравнениям этих прямых:

-x₁+8x₂≤12, (1)

x₁-2x₂≤2, (4)

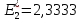, , (11)

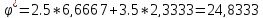, (12)

Ответ: ,;
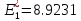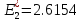