- •Оглавление
- •Исходные данные
- •Задание №1. Графоаналитическое решение озлп
- •Задание № 2. Задача о коммивояжере. Метод ветвей и границ
- •Задание №3. Оптимизация дискретных управлений дискретными динамическими объектами методом динамического программирования р. Беллмана
- •Задание №4. Синтез непрерывного оптимального управления с помощью уравнения Эйлера
- •Задание №5. Синтез непрерывных оптимальных уравнений с помощью уравнения Эйлера-Пуассона
Оглавление
Исходные данные 5
Задание №1. Графоаналитическое решение ОЗЛП 6
Задание № 2. Задача о коммивояжере. Метод ветвей и границ 10
Задание №3. Оптимизация дискретных управлений дискретными динамическими объектами методом динамического программирования Р. Беллмана 20
Задание №4. Синтез непрерывного оптимального управления с помощью уравнения Эйлера 24
Задание №5. Синтез непрерывных оптимальных уравнений с помощью уравнения Эйлера-Пуассона 27
Исходные данные
К заданию №1.
|
№ |
C1 |
C2 |
B1 |
B2 |
A11 |
A12 |
A21 |
A22 |
|
222 |
5 |
1 |
4 |
4 |
2 |
-2 |
2 |
6 |
К заданию №2.
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
С = |
1 |
∞ |
2 |
4 |
5 |
3 |
1 |
|
2 |
1 |
∞ |
1 |
2 |
7 |
6 |
|
|
3 |
6 |
5 |
∞ |
1 |
4 |
3 |
|
|
4 |
1 |
7 |
6 |
∞ |
5 |
1 |
|
|
5 |
6 |
5 |
2 |
3 |
∞ |
4 |
|
|
6 |
1 |
3 |
5 |
6 |
1 |
∞ |
К заданию №3.
|
№ |
A |
B |
α |
β |
γ |
|
122 |
1 |
0,25 |
2 |
1,5 |
8 |
К заданию №4.
|
№ |
A |
B |
α2 |
|
122 |
0,5 |
1 |
3/4 |
К заданию №5.
|
№ |
k |
γ |
|
122 |
44 |
22 |
Задание №1. Графоаналитическое решение озлп
1. Математическая постановка ОЗЛП:
φ=5x1+x2→max, (0)
2x1-2x2≤4, (1)
2x1+6x2≤4, (2)
x1≥0, (3)
x2≥0, (4)
BD: 2x1-2x2=4, (1’)
CD: 2x1+6x2=4, (2’)
AC: x1=0, (3’)
AB: x2=0, (4’)
2. Записываем уравнение граничных линий допустимого многоугольника (1’) - (4’).
На плоскости (x1, x2) строим граничные линии.
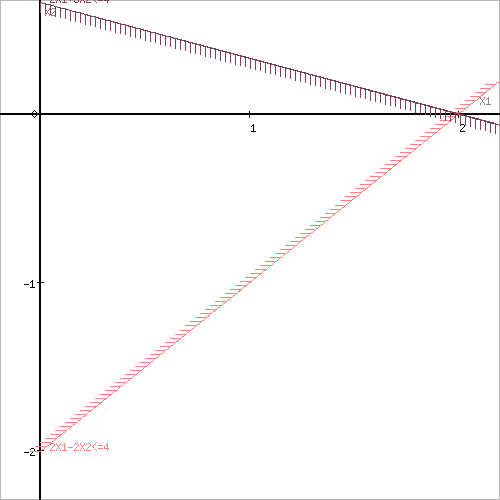
3. Строим линию, пересекающую область φ.
 ,
(5)
,
(5)
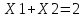 ,
(6)
,
(6)
4. Находим градиент целевой функции:
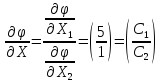 ,
(7)
,
(7)
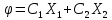 ,
(8)
,
(8)
Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.
Обозначим границы области многоугольника решений.
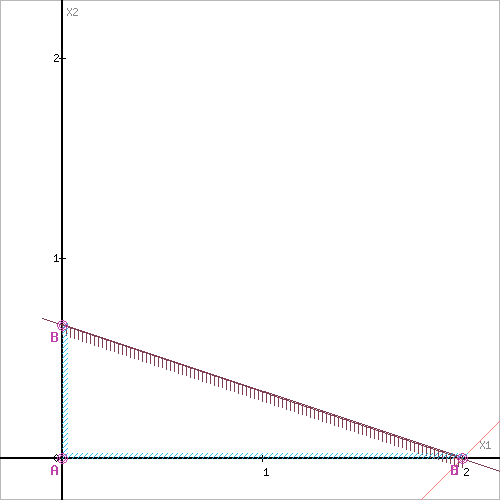
Рассмотрим целевую функцию задачи φ=5x1+x2→max. Построим прямую, отвечающую значению функции φ=0: F=5x1+x2=0. Будем двигать эту прямую параллельным образом до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.
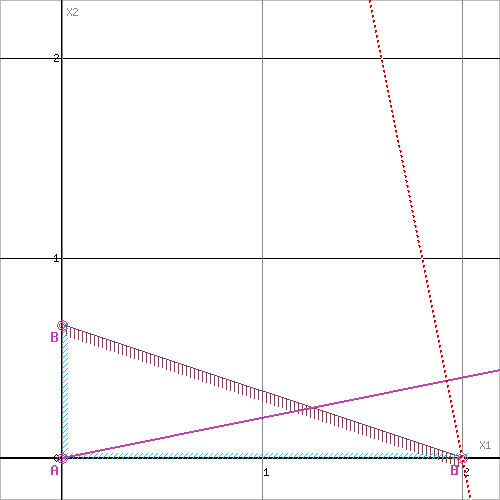
Из
рисунка видно, что оптимальная точка
D* равная
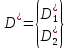 ,
находится на пересечении линий BD
и CD и ее координаты
определяются путем решения одноименных
уравнений (1’) и (2’).
,
находится на пересечении линий BD
и CD и ее координаты
определяются путем решения одноименных
уравнений (1’) и (2’).
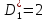 ,
,
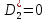 ,
(9)
,
(9)
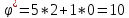 ,
(10)
,
(10)
Ответ:
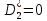 ;
;
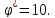
Задание № 2. Задача о коммивояжере. Метод ветвей и границ
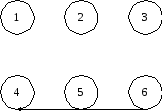
Расстояния между пунктами заданы матрицей:
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
С = |
1 |
∞ |
2 |
4 |
5 |
3 |
1 |
|
2 |
1 |
∞ |
1 |
2 |
7 |
6 |
|
|
3 |
6 |
5 |
∞ |
1 |
4 |
3 |
|
|
4 |
1 |
7 |
6 |
∞ |
5 |
1 |
|
|
5 |
6 |
5 |
2 |
3 |
∞ |
4 |
|
|
6 |
1 |
3 |
5 |
6 |
1 |
∞ |
Решение задачи о коммивояжере методом ветвей и границ начинается с приведения матрицы (вычитания из каждой строки (столбца) матрицы C минимального элемента этой строки (столбца).
Произведем приведение матрицы C по строкам:
hν= min(i) hνi
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
hν |
|
С’ = |
1 |
∞ |
4 |
1 |
3 |
2 |
1 |
1 |
|
2 |
2 |
∞ |
4 |
1 |
5 |
6 |
1 |
|
|
3 |
7 |
1 |
∞ |
4 |
6 |
5 |
1 |
|
|
4 |
4 |
6 |
7 |
∞ |
1 |
3 |
1 |
|
|
5 |
3 |
2 |
1 |
6 |
∞ |
1 |
2 |
|
|
6 |
0 |
5 |
3 |
2 |
4 |
∞ |
1 |
Произведем приведение матрицы C по столбцам:
gi = min(υ) gνi
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
С’ = |
1 |
∞ |
3 |
0 |
2 |
1 |
0 |
|
2 |
2 |
∞ |
3 |
0 |
4 |
5 |
|
|
3 |
7 |
0 |
∞ |
3 |
6 |
5 |
|
|
4 |
4 |
6 |
6 |
∞ |
0 |
2 |
|
|
5 |
3 |
1 |
0 |
5 |
∞ |
0 |
|
|
6 |
0 |
4 |
2 |
1 |
3 |
∞ |
|
|
|
gi |
0 |
1 |
0 |
0 |
0 |
0 |
В итоге получаем полностью приведенную (редуцированную) матрицу:
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
hν |
|
С0 = |
1 |
∞ |
3 |
0 |
2 |
1 |
0 |
1 |
|
2 |
2 |
∞ |
3 |
0 |
4 |
5 |
1 |
|
|
3 |
7 |
0 |
∞ |
3 |
6 |
5 |
1 |
|
|
4 |
4 |
6 |
6 |
∞ |
0 |
2 |
1 |
|
|
5 |
3 |
1 |
0 |
5 |
∞ |
0 |
2 |
|
|
6 |
0 |
4 |
2 |
1 |
3 |
∞ |
1 |
|
|
|
gi |
0 |
1 |
0 |
0 |
0 |
0 |
|
Величины hν и gi называются константами приведения.
Нижняя
граница цикла: d0=8
(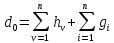 ).
).
Шаг №1.
Определяем
ребро ветвления и разобьем все
множество допустимых значений Q0
относительно этого ребра на два
непересекающихся подмножества (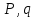 )
и (
)
и (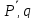 ),
т.е.
),
т.е.
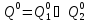 ,
где
,
где
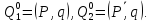
В приведенной матрице исследуем все нулевые переходы.
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
αν |
|
C0 = |
1 |
∞ |
0(1) |
3 |
4 |
2 |
0(0) |
0 |
|
2 |
0(0) |
∞ |
0(0) |
1 |
6 |
5 |
0 |
|
|
3 |
5 |
3 |
∞ |
0(3) |
3 |
2 |
2 |
|
|
4 |
0(0) |
5 |
5 |
∞ |
4 |
0(0) |
0 |
|
|
5 |
4 |
2 |
0(1) |
1 |
∞ |
2 |
1 |
|
|
6 |
0(0) |
1 |
4 |
5 |
0(2) |
∞ |
0 |
|
|
|
βi |
0 |
1 |
0 |
1 |
2 |
0 |
|
Наибольшая сумма констант приведения равна
υ34= α3 + β4 =2+1=3, следовательно,
множество
разбивается на два подмножества
 и
и
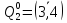 .
.
Оценка
длины цикла:
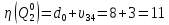 .
.
В результате получим другую сокращенную матрицу (5x5), которая подлежит операции приведения.
После операции приведения сокращенная матрица будет иметь вид:
|
|
|
1 |
2 |
3 |
5 |
6 |
hν |
|
|
1 |
∞ |
0 |
3 |
2 |
0 |
0 |
|
|
2 |
0 |
∞ |
0 |
6 |
5 |
0 |
|
C1= |
4 |
0 |
5 |
∞ |
4 |
0 |
0 |
|
|
5 |
4 |
2 |
0 |
∞ |
2 |
0 |
|
|
6 |
0 |
1 |
4 |
0 |
∞ |
0 |
|
|
gi |
0 |
0 |
0 |
0 |
0 |
|
d1=0
Шаг №2.
Определяем
ребро ветвления и разобьем все
множество допустимых значений Q1
относительно этого ребра на два
непересекающихся подмножества
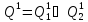 .
.
В приведенной матрице исследуем все нулевые переходы.
|
|
|
1 |
2 |
3 |
5 |
6 |
αν |
|
|
1 |
∞ |
0(1) |
3 |
2 |
0(0) |
0 |
|
|
2 |
0(0) |
∞ |
0(0) |
6 |
5 |
0 |
|
C1= |
4 |
0(0) |
5 |
∞ |
4 |
0(0) |
0 |
|
|
5 |
4 |
2 |
0(2) |
∞ |
2 |
2 |
|
|
6 |
0(0) |
1 |
4 |
0(2) |
∞ |
0 |
|
|
βi |
0 |
1 |
0 |
2 |
0 |
|
Наибольшая сумма констант приведения равна
υ53=2+0=2, следовательно,
множество
разбивается на два подмножества
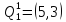 и
и
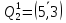 .
.
Оценка
длины цикла:
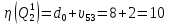 .
.
Оценка
на перспективном множестве:
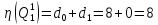
В результате получим другую сокращенную матрицу (4x4), которая подлежит операции приведения.
После операции приведения сокращенная матрица будет иметь вид:
|
|
|
1 |
2 |
5 |
6 |
hν |
|
C2 = |
1 |
∞ |
0 |
2 |
0 |
0 |
|
2 |
0 |
∞ |
6 |
5 |
0 |
|
|
4 |
0 |
5 |
4 |
0 |
0 |
|
|
6 |
0 |
1 |
0 |
∞ |
0 |
|
|
|
gi |
0 |
0 |
0 |
0 |
|
d2=0
Шаг №3.
Определяем
ребро ветвления и разобьем все
множество допустимых значений Q2
относительно этого ребра на два
непересекающихся подмножества
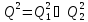 .
.
В приведенной матрице исследуем все нулевые переходы.
|
|
|
1 |
2 |
5 |
6 |
αν |
|
C2 = |
1 |
∞ |
0(1) |
2 |
0(0) |
0 |
|
2 |
0(5) |
∞ |
6 |
5 |
5 |
|
|
4 |
0(0) |
5 |
∞ |
0(0) |
0 |
|
|
6 |
0(0) |
1 |
0(2) |
∞ |
0 |
|
|
|
βi |
0 |
1 |
2 |
0 |
|
Наибольшая сумма констант приведения равна
υ21=5+0=5, следовательно,
множество
разбивается на два подмножества
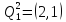 и
и
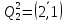 .
.
Оценка
длины цикла:
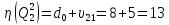 .
.
Оценка
на перспективном множестве:
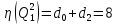
В результате получим другую сокращенную матрицу (3x3), которая подлежит операции приведения.
После операции приведения сокращенная матрица будет иметь вид:
|
|
|
2 |
5 |
6 |
hν |
|
|
1 |
∞ |
2 |
0 |
0 |
|
C3 = |
4 |
5 |
∞ |
0 |
0 |
|
|
6 |
1 |
0 |
∞ |
0 |
|
|
gi |
1 |
0 |
0 |
|
d3=1
Шаг №4.
Определяем
ребро ветвления и разобьем все
множество допустимых значений Q3
относительно этого ребра на два
непересекающихся подмножества
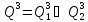 .
.
В приведенной матрице исследуем все нулевые переходы.
|
|
|
2 |
5 |
6 |
αν |
|
|
1 |
∞ |
2 |
0(2) |
2 |
|
C3 = |
4 |
4 |
∞ |
0(4) |
4 |
|
|
6 |
0(4) |
0(2) |
∞ |
0 |
|
|
βi |
4 |
2 |
0 |
|
Наибольшая сумма констант приведения равна
υ46=4+0=4, следовательно,
множество
разбивается на два подмножества
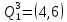 и
и
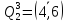 .
.
Оценка
длины цикла:
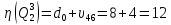 .
.
Оценка
на перспективном множестве:
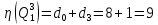
В результате получим другую сокращенную матрицу (2x2), которая подлежит операции приведения.
После операции приведения сокращенная матрица будет иметь вид:
|
|
|
2 |
5 |
hν |
|
C4 = |
1 |
∞ |
2 |
2 |
|
6 |
0 |
0 |
0 |
|
|
|
gi |
0 |
0 |
|
d4=2
В
соответствии с этой матрицей включаем
в маршрут
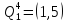 и
и
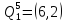 .
.
Ответ: l* =C34+C46+C62+C21+C15+C53=1+1+3+1+3+2=11.
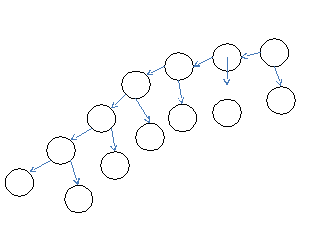
Дерево решения имеет следующий вид: