Пример 2.19. Определить эквивалентные активное и реактивное сопротивления цепи, если мгновенные значения напряжения и тока на ее входных зажимах соответственно равны

В, А.

Р е ш е н и е.

Ом,

т.е. R = 40 Ом, x = 30 Ом.

Знак минус перед мнимой частью комплексного сопротивления говорит о том, что суммарное реактивное сопротивление цепи носит емкостный характер. Это видно и из условия задачи. Ток опережает напряжение, его начальная фаза больше.

Пример 2.20. Определить комплексную проводимость цепи, состоящей из последовательно соединенных активного R и реактивного x сопротивлений.

Решение.

где , .

2.16. О расчете цепей синусоидального тока

Как следует из изложенного теоретического материала и приведенных примеров, при анализе цепей синусоидального тока широко применяются векторные диаграммы и комплексные числа. Сами по себе векторные диаграммы зачастую служат для иллюстрации результатов теоретических исследований и решения задач. Они помогают лучше понять сущность изучаемых процессов и наглядно представить соотношения и связи напряжений и токов на различных участках с параметрами цепи.

Во многих случаях векторные диаграммы, построенные предварительно по изложенным выше правилам без каких-либо вычислений, являются основой для вывода из них конкретной методики решения данной задачи. Возможны также привязка векторной диаграммы к комплексным осям, выражение векторов комплексными числами и дальнейший расчет в символической форме. Принципиального отличия между методом векторных диаграмм и символическим нет. Как мы видели раньше, за аналитическими действиями с комплексными числами кроются определенные геометрические операции с векторами.

Следует также помнить, что никакого физического содержания векторы и комплексные числа в себе не несут. Это чисто математические абстракции, необходимые для анализа.

Символический метод базируется на законах Ома и Кирхгофа, которые в символической форме записываются точно так же, как в цепях постоянного тока. Поэтому все изложенные ранее методы расчета цепей постоянного тока, вытекающие из этих законов, применимы и для расчета в символической форме цепей синусоидального тока.

Пример 2.21. Рассчитать комплексные сопротивления цепей, изображенных на рис. 2.39, а и б.

Решение. Сопротивление каждой ветви записываем в символической форме и применяем формулу, известную из теории цепей постоянного тока.

Для схемы, изображенной на рис. 2.39, а:

Ом, Ом,

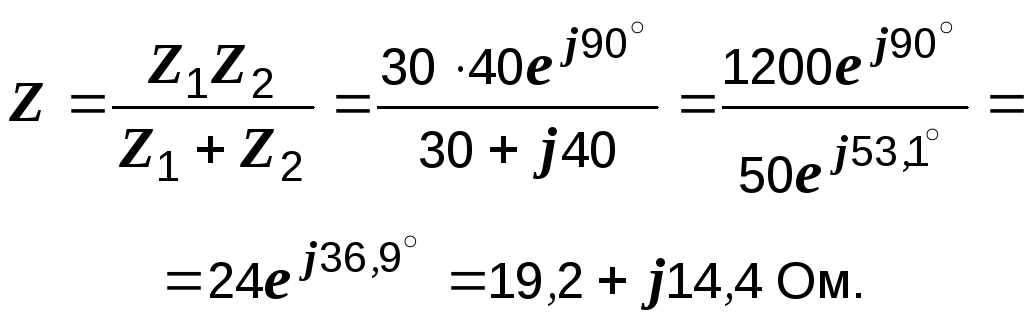
Смысл полученного результата заключается в том, что рассматриваемая параллельная цепь может быть заменена эквивалентной последовательной с активным сопротивлением 19,2 Ом и индуктивным 14,4 Ом.

Для схемы на рис. 2.39, б:

Ом.

Пример 2.22. Рассчитать цепь, приведенную на рис. 2.40.

Р е ш е н и е. Находим комплексные сопротивления участков:

Ом,

Ом,

Ом

Ом

Определяем комплексные токи ветвей:

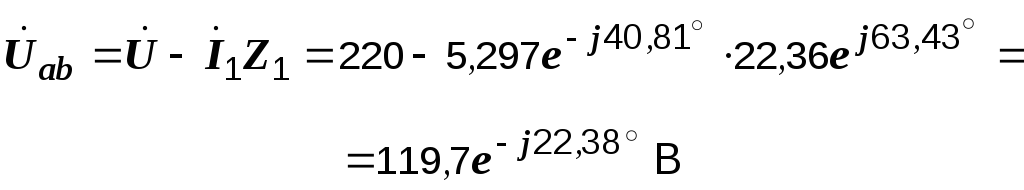
А,

А,

А.

Численные значения токов:

А, А, А.

Для проверки правильности расчета используем первый закон Кирхгофа в символической форме .

Смотрим: А.

В пределах точности расчета закон выполняется.

2.17. Резонансы в электрических цепях

Резонансом называют режим, когда в цепи, содержащей индуктивности и емкости, ток совпадает по фазе с напряжением. Входные реактивные сопротивление и проводимость равны нулю: x = ImZ = 0 и B = ImY = 0. Цепь носит чисто активный характер: Z = R; сдвиг фаз отсутствует (j = 0).

В цепи, содержащей последовательно соединенные участки с индуктивным и емкостным характерами сопротивлений, резонанс называется резонансом напряжений. Рассмотрим простейшую цепь такого вида (рис. 2.23), которую часто называют последовательным контуром. Для нее резонанс наступает при x = x_L – x_C = 0 или x_L = x_C, откуда

(2.33)

Напряжения на индуктивности и емкости в этом режиме равны по величине и, находясь в противофазе, компенсируют друг друга. Все приложенное к цепи напряжение приходится на ее активное сопротивление (рис. 2.42, а).

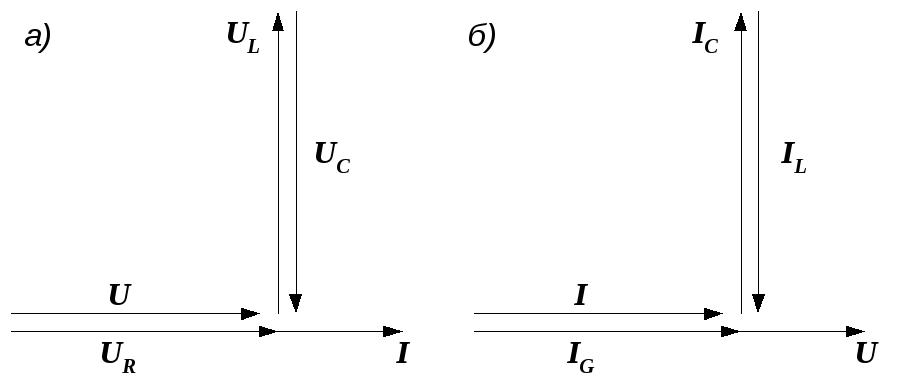
Рис. 2.42. Векторные диаграммы при резонансе напряжений (а) и токов (б)

Напряжения на индуктивности и емкости могут значительно превышать напряжения на входе цепи. Их отношение, называемое добротностью контура Q, определяется величинами индуктивного (или емкостного) и активного сопротивлений

.

Добротность показывает, во сколько раз напряжения на индуктивности и емкости при резонансе превышают напряжение, приложенное к цепи. В радиотехнических цепях она может достигать нескольких сотен единиц.

Из условия (2.33) следует, что резонанса можно достичь, изменяя любой из параметров – частоту, индуктивность, емкость. При этом меняются реактивное и полное сопротивления цепи, а вследствие этого – ток, напряжение на элементах и сдвиг фаз. Не приводя анализа формул, показываем графические зависимости некоторых из этих величин от емкости (рис. 2.43). Емкость , при которой наступает резонанс, можно определить из формулы (2.33):

.

Если, например, индуктивность контура L = 0,2 Гн, то при частоте 50 Гц, резонанс наступит при емкости

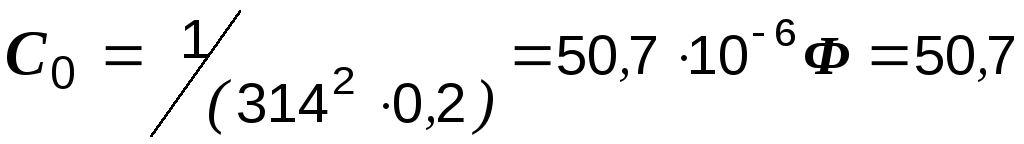мкФ.

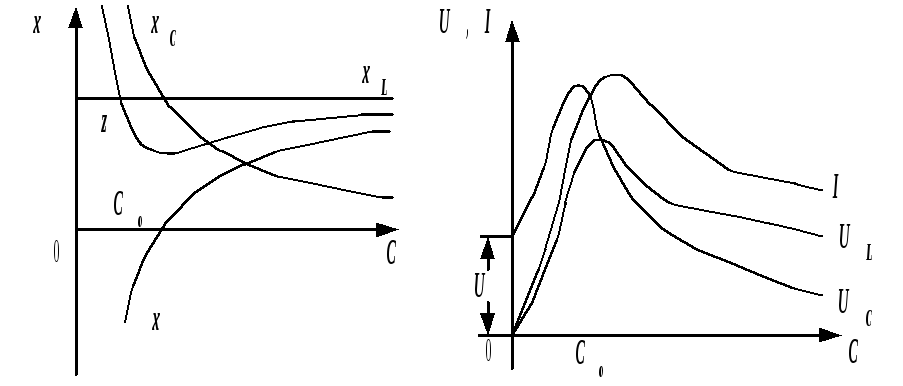
Рис. 2.43. Зависимости параметров режима от емкости

Аналогичные рассуждения можно провести и для цепи, состоящей из параллельно соединенных R, L и C (рис. 2.31, а). Векторная диаграмма ее резонансного режима приведена на рис. 2.42, б.

Рассмотрим теперь более сложную цепь с двумя параллельными ветвями, содержащими активные и реактивные сопротивления (рис. 2.44, а).

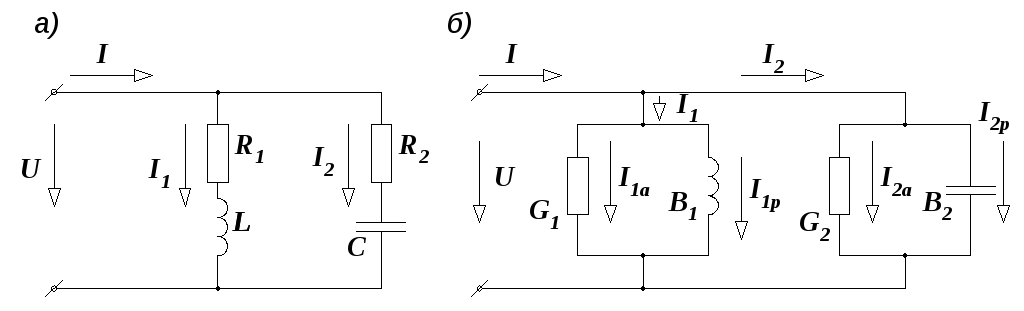
Рис. 2.44. Разветвленная цепь (а) и ее эквивалентная схема (б)

Для нее условием резонанса является равенство нулю ее реактивной проводимости: ImY = 0. Это равенство означает, что мы должны мнимую часть комплексного выражения Y приравнять к нулю.

Определяем комплексную проводимость цепи. Она равна сумме комплексных проводимостей ветвей:

.

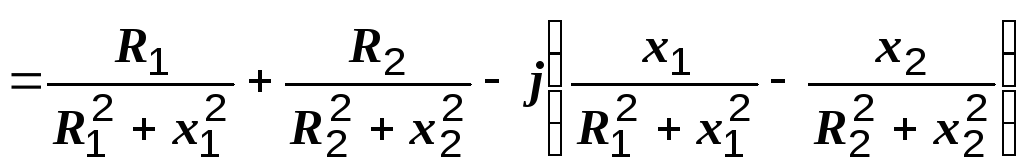Приравнивая к нулю выражение, стоящее в круглых скобках, получаем:

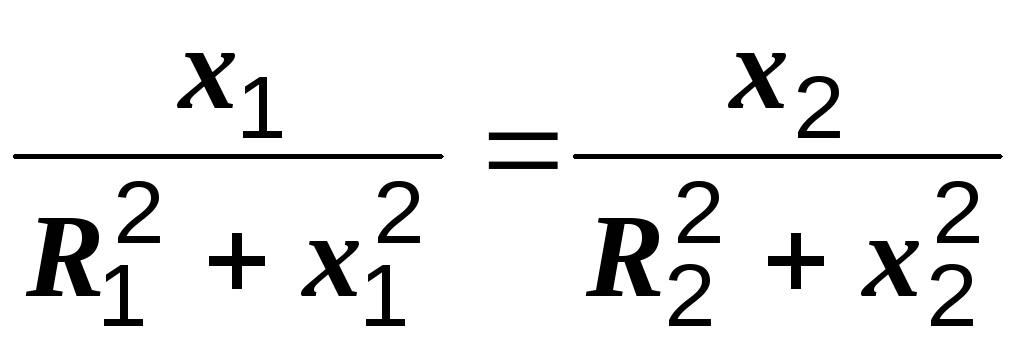или 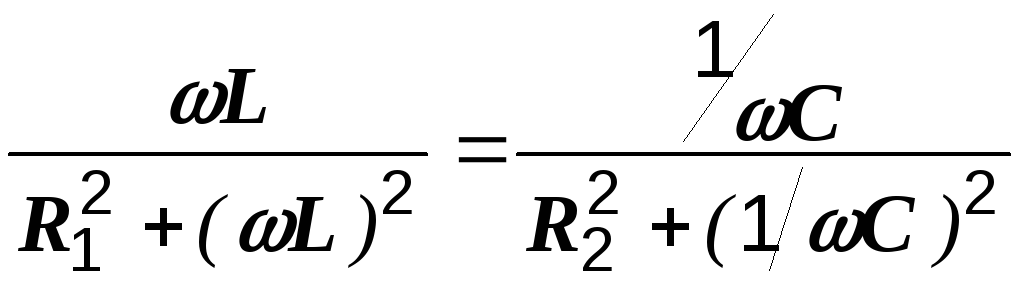. (2.34)

Левая и правая части последнего выражения представляют собой не что иное, как реактивные проводимости первой и второй ветвей B₁ и B₂. Заменяя схему на рис. 2.44, а эквивалентной (рис. 2.44, б), параметры которой вычисляем по формуле (2.31), и используя условие резонанса (B = B₁ – B₂ = 0), снова приходим к выражению (2.34).

Схеме на рис. 2.44, б соответствует векторная диаграмма, приведенная на рис. 2.45.

Резонанс в разветвленной цепи называется резонансом токов. Реактивные составляющие токов параллельных ветвей противоположны по фазе, равны по величине и компенсируют друг друга, а сумма активных составляющих токов ветвей дает общий ток.

Рис. 2.45. Векторная диаграмма резонансного режима разветвленной цепи

Пример 2.23. Считая R₂ и x₃ известными, определить величину x₁, при которой в цепи наступит резонанс напряжений (рис. 2.46, а). Для резонансного режима построить векторную диаграмму.

Рис. 70. Векторная диаграмма резонансного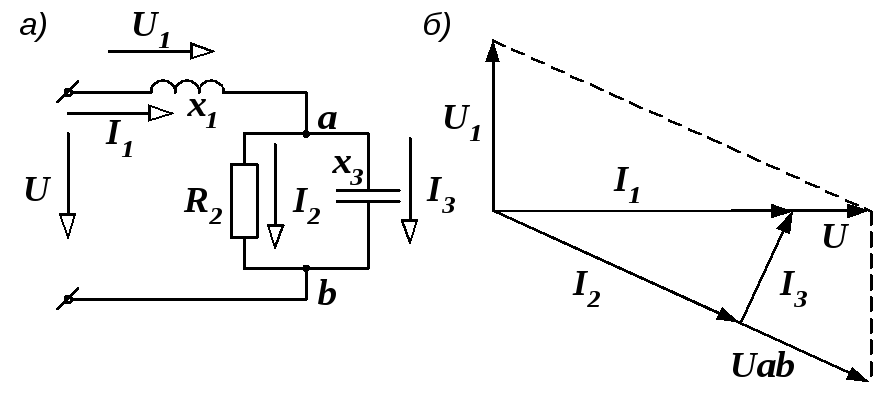

Рис. 2.46. Электрическая цепь и ее векторная диаграмма

Решение. При резонансе напряжение U₁ на индуктивном сопротивлении x₁ равно реактивной составляющей напряжения U_ab: I₁x₁ = I₁x_ab, откуда x₁ = x_ab. Последнее есть реактивное сопротивление последовательной эквивалентной схемы замещения участка ab:

.

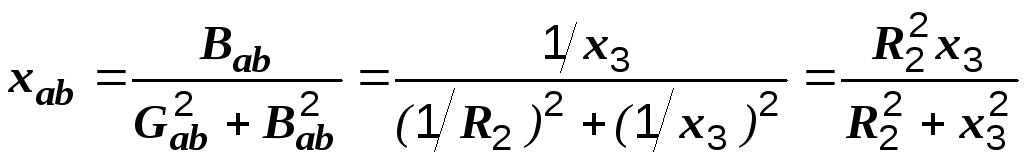Задача может быть решена и символическим методом. В соответствии с условием резонанса напряжений, мы должны приравнять к нулю мнимую часть комплексного сопротивления цепи. Величина последнего равна

.

Сумму всех коэффициентов при мнимой единице приравниваем к нулю:

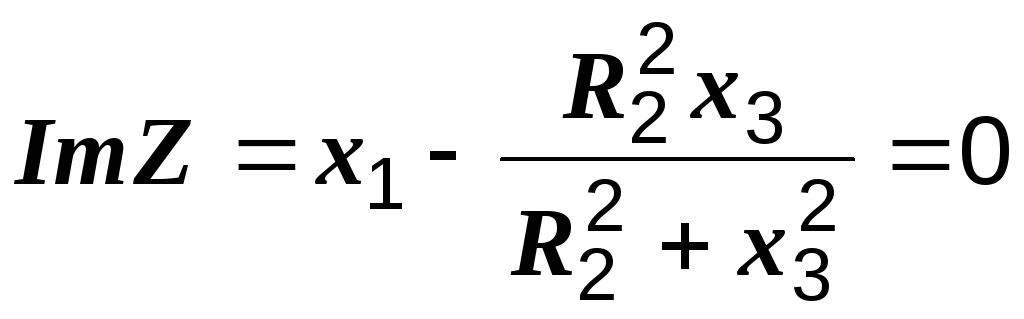, откуда .

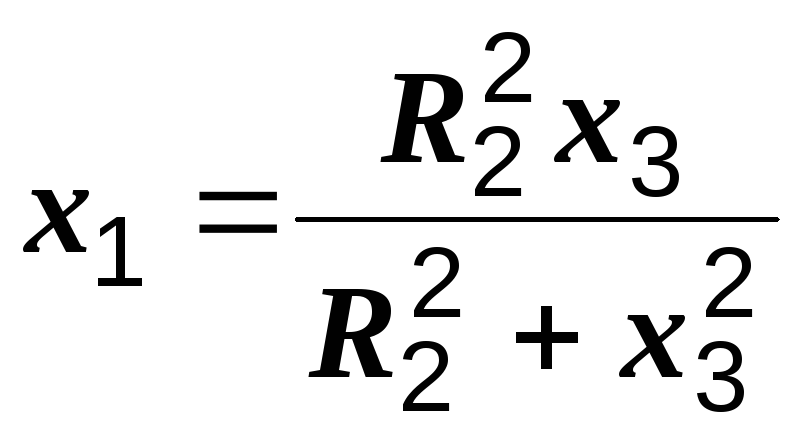Построение векторной диаграммы начинаем с вектора I₁ (рис. 2.46, б). В том же направлении проводим вектор приложенного к цепи напряжения U – при резонансе они совпадают по фазе. Напряжение на индуктивности опережает ток на 90°, его вектор U₁ направляем вверх. Вектор U_ab проводим так, чтобы он в сумме с вектором U₁ давал вектор U. Ток I₂ совпадает по фазе с U_ab, а I₃ опережает последний на 90°. В сумме векторы I₂ и I₃ дают вектор I₁.