
- •2.Случайные события , их классификация. Действия над событиями
- •3.Классическое, статистическое и геометрическое опр. Вероятности.
- •5.Теорема сложения вероятностей несовместных событий и ее следствия.
- •7. Теорема сложения вероятностей совместных событий.
- •8. Вероятность появления хотя бы одного из n событий, независимых в совокупности.
- •6.Зависимые и независимые события. Условная вероятность. Теорема умножения вероятностей.
- •9.Формула полной вероятности и формула Байеса
- •10.Повторные независимые испытания. Ф-ла Бернулли.
- •11. Наивероятнейшее число появлений события в схеме Бернулли.
- •Вопрос 12. Локальная и интегральная теоремы Лапласа.
- •13.Формула Пуассона для редких событий.
- •14. Дискретная случайная величина, ее закон распределения. Многоугольник распределения.
- •15. Функция распределения вероятностей случайной величины и ее свойства.
- •16. Математическое ожидание дискретной случайной величины и его свойства.
- •17. Дисперсия дсв и ее св-ва. Среднее квадр. Отклонение.
- •28. Вер-ть попад-я в зад. Интервал нормально распред. Случ. В-ны. В-сть зад. Откл-я. Правило трех сигм.
- •29. Моменты случайной величины. Асимметрия. Эксцесс.
- •41. Интервальные оценки числовых характеристик случайной величины. Доверительная вероятность. Доверительный интервал.
41. Интервальные оценки числовых характеристик случайной величины. Доверительная вероятность. Доверительный интервал.
Пусть сделана выборка объема n. Для оценки распределения СВ Х генеральной совокупности применяются точечные оценки параметров распределения генеральной совокупности и интервальные оценки.
Будем
предполагать, что пр-к в ген. сов-ти
распр. по норм. закону и считаем, что
наша оценка МХ несмещенная. Тогда М(Х с
крышкой)=х0.
Тогда, восп. формулой
![]()
Из
формулы след., что неизв. вел. ср.ген.выборки
х0
содержится в инт-ле (![]() )
с вер-тью, равной р, где р вычисл по
формуле:
)
с вер-тью, равной р, где р вычисл по
формуле:
![]() -
доверительная вер-ть. Восп. таблицей
значений ф-ии Лапласа (Ф), по известной
вер-ти можно опр. значение аргумента
ф-ии, и рассчитать величину
-
доверительная вер-ть. Восп. таблицей
значений ф-ии Лапласа (Ф), по известной
вер-ти можно опр. значение аргумента
ф-ии, и рассчитать величину
![]() .
.
Этот
инт-л![]() наз. доверительным для средней
наз. доверительным для средней![]() .
Как правило, в задачах дов. вер-ть задана
и необх. найти довер. инт-л. Обычно на
практике доверительная вер-ть берется
на Ур-не (0,95; 0,99; 0,999)
.
Как правило, в задачах дов. вер-ть задана
и необх. найти довер. инт-л. Обычно на
практике доверительная вер-ть берется
на Ур-не (0,95; 0,99; 0,999)
Т.о.
интервальной
оценкой
(доверительным интервалом) для оценки
некоторого параметра
(тэта), например
![]() ,
называется интервал, в котором с заранее
заданной вероятностью Р=1-
содержится оцениваемый параметр.
,
называется интервал, в котором с заранее
заданной вероятностью Р=1-
содержится оцениваемый параметр.
42.
Основные понятия регрессионного и
корреляционного анализа. Функцион.
зависимость (y=f(x))
м-ду величинами X
и Y
закл. в том,
что
каждому значению одной переменной
соответствует вполне опред. значение
другой. Статистической
наз.т зависимость, при которой изменение
одной из величин влечет изменение
распределения другой. В частности,статистическая
зависимость проявляется в том, что при
изменении одной из величин изменяется
среднее значение другой. В этом случае
стат. зав-ть наз. корреляционной
зав-тью.Корреляционной
(или регрессионной) зависимостью между
двумя переменными величинами называется
функциональная зависимость между
значениями одной из них и условным
математическим ожиданием другой.
Условное мат. ожидание Mx
(Y)
СВ Y есть
функция от x
: Mx
(Y)
f (x)
, которую называют функцией регрессии
Y на
X .
Корреляц. зависимостью Y
от X
называется
функц. зависимость условной средней
![]() x
от x .
Уравнение y
f
xназ.
уравн-ем регрессии Y
на X
. Функция f
xназ.
регрессией Y
на X
, а ее график
– линией регрессии СВ Y
на СВ X
. Осн. задачи
теории корреляции: 1. Установл. формы
корреляционной связи; 2. Оценка тесноты
корреляционной связи Y
от X
, кот.
оценивается величиной рассеяния значений
Y около
Yx.
Большое рассеяние означает слабую
зависимость Y
от X
либо вообще
отсутствие таковой. Малое рассеяние
указывает на существование достаточно
сильной зависимости Y
от X
. Важной с
точки зрения приложений является
ситуация, когда обе функции регрессии
f (x),yявляются
линейными. Тогда говорят, что СВ X
и Y
связаны
линейной корреляц. зав-стью (линейной
корреляцией).
x
от x .
Уравнение y
f
xназ.
уравн-ем регрессии Y
на X
. Функция f
xназ.
регрессией Y
на X
, а ее график
– линией регрессии СВ Y
на СВ X
. Осн. задачи
теории корреляции: 1. Установл. формы
корреляционной связи; 2. Оценка тесноты
корреляционной связи Y
от X
, кот.
оценивается величиной рассеяния значений
Y около
Yx.
Большое рассеяние означает слабую
зависимость Y
от X
либо вообще
отсутствие таковой. Малое рассеяние
указывает на существование достаточно
сильной зависимости Y
от X
. Важной с
точки зрения приложений является
ситуация, когда обе функции регрессии
f (x),yявляются
линейными. Тогда говорят, что СВ X
и Y
связаны
линейной корреляц. зав-стью (линейной
корреляцией).
44.
Коэффициент линейной корреляции и его
свойства.
![]() - корреляционный момент (ковариация),
где K(X
,Y
) M{[X
M(X
)][Y
M(Y)]}
Две случайные величины X
и Y
называются
коррелированными, если их коэф-т
корреляции отличен от нуля. СВ X
и Y
называются
некоррелированными, если их корреляционный
момент равен нулю.
- корреляционный момент (ковариация),
где K(X
,Y
) M{[X
M(X
)][Y
M(Y)]}
Две случайные величины X
и Y
называются
коррелированными, если их коэф-т
корреляции отличен от нуля. СВ X
и Y
называются
некоррелированными, если их корреляционный
момент равен нулю.
![]() выборочный коэф. коррел. Свойства коэф-та
корреляции: 1. Коэф-т корреляции
выборочный коэф. коррел. Свойства коэф-та
корреляции: 1. Коэф-т корреляции
![]() принимает значения на отрезке [1;1],
т.е. 1 1 в 1r
1; 2.Если
все значения переменных увеличить
(уменьшить) на одно и то же число или в
одно и то же число раз, то величина
выборочного коэф-та корреляции не
изменится. 3.При 1 r
= ±1 корреляц.
связь представл. линейную функц.
зависимость. При этом линии регрессии
Y на
X и
X на
Y совпадают,
все наблюдаемые значения располагаются
на общей прямой. 4.Если с ростом значений
одной СВ значения второй возрастают,
то 0 в r >
, если убывают, то 0 в r
< . 5.При 0 в
r =
линейная корреляц. связь отсутствует,
групповые средние переменных совпадают
с их общими средними, а линии регрессии
Y на
X и
X на
Y параллельны
осям координат. Выборочный коэф-т
корреляции r
является
оценкой генерального коэф-та корреляции
принимает значения на отрезке [1;1],
т.е. 1 1 в 1r
1; 2.Если
все значения переменных увеличить
(уменьшить) на одно и то же число или в
одно и то же число раз, то величина
выборочного коэф-та корреляции не
изменится. 3.При 1 r
= ±1 корреляц.
связь представл. линейную функц.
зависимость. При этом линии регрессии
Y на
X и
X на
Y совпадают,
все наблюдаемые значения располагаются
на общей прямой. 4.Если с ростом значений
одной СВ значения второй возрастают,
то 0 в r >
, если убывают, то 0 в r
< . 5.При 0 в
r =
линейная корреляц. связь отсутствует,
групповые средние переменных совпадают
с их общими средними, а линии регрессии
Y на
X и
X на
Y параллельны
осям координат. Выборочный коэф-т
корреляции r
является
оценкой генерального коэф-та корреляции
45.
Стат. гипотеза. Стат. критерий проверки
гипотез. Ошибки 1 и 2 рода. Критич. область.
Стат. гипотеза
– любое предпол. относит. генер. сов-ти,
кот. проверяется путем анализа данных
выборки. Выдвинутую гипотезу наз.
основной или нулевой Но. наряду с Но
рассм. противоречащую ей гипотезу Н1,
кот. наз-ся альтернативной или
конкурирующей. Выдвинутая гипотеза
должна быть проверена стат. методами.
По итогам проверки гипотеза либо
принимается, либо отклоняется. При этом
могут быть допущены ошибки 2 родов:
ошибки 1 рода сост. в том, что будет
принята гипотеза Н1, в то время как верной
явл. гипотеза Но. Вер-ть ошибки 1 рода
обозн.![]() и ее наз. уровнем
и ее наз. уровнем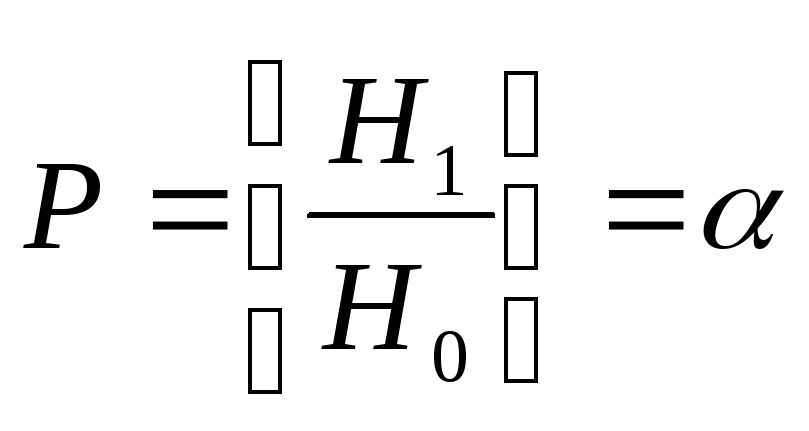 .
Ошибка 2 рода сост. в том, что будет
принята гипотеза Но, в то время как
верной явл. гипотеза Н1. Вероятность ош.
2 рода обозн.
.
Ошибка 2 рода сост. в том, что будет
принята гипотеза Но, в то время как
верной явл. гипотеза Н1. Вероятность ош.
2 рода обозн.![]()
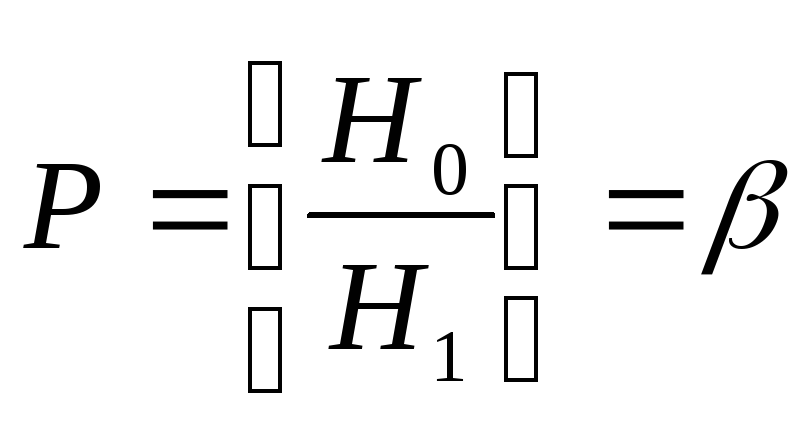 .
Стат. критерием наз. СВ К, кот. служит
для проверки нулевой гипотезы. Множ-во
всех возм. значений критерия К разбивается
на 2 непересек. подмнож-ва – критич.
область (мн-во значений критерия, при
кот. нулевую гипотезу отвергают) и обл.
принятия гипотезы (мн-во значений
критерия, при кот. нулевую принимают).
По данным выб-ки выч-ся значение К
наблюдаемое, кот. наз. наблюдаемым
знач-ем. Правило проверки стат. гипот.:если
значение К набл. попадает в обл. принятия,
то Но приним-ся; если значен. К набл.
попадает в критич. обл., то гип. Но
отверг-ся. Мощностью критерия наз. вер-ть
того, что будет принята конкурир. гипотеза
Н1 если она явл. верной. Если
.
Стат. критерием наз. СВ К, кот. служит
для проверки нулевой гипотезы. Множ-во
всех возм. значений критерия К разбивается
на 2 непересек. подмнож-ва – критич.
область (мн-во значений критерия, при
кот. нулевую гипотезу отвергают) и обл.
принятия гипотезы (мн-во значений
критерия, при кот. нулевую принимают).
По данным выб-ки выч-ся значение К
наблюдаемое, кот. наз. наблюдаемым
знач-ем. Правило проверки стат. гипот.:если
значение К набл. попадает в обл. принятия,
то Но приним-ся; если значен. К набл.
попадает в критич. обл., то гип. Но
отверг-ся. Мощностью критерия наз. вер-ть
того, что будет принята конкурир. гипотеза
Н1 если она явл. верной. Если![]() -
вер-ть ошибки 2 рода, то мощн-ть критерия
= 1-
-
вер-ть ошибки 2 рода, то мощн-ть критерия
= 1-![]()
46.
Проверка гипотезы о математическом
ожидании нормально распределенной
случайной величины. Пусть
имеется нормально распр. СВ ,,
опред. на мн-стве объектов некот.
генер.сов-сти. Известно, что D
= 2.
Мат. ожидание M
неизвестно. Допустим, что M
= a,
где a
– некот. число. Будем считать также, что
имеется другая информация, что M
= a1,
где a1
>
a.
I. Выдвиг. нулевую гипотезу H0:
M
= a
при конкур. гипотезе H1:
M
= a1.
Делаем выборку объема n:
x1,
x2,...,
xn
.
В основе проверки лежит тот факт, что
случ. вел-на
![]() (выбор. средняя) распр-на по норм. закону
с дисперсией 2/n
и мат.ож-ем, равным a
в случае справ-сти H0,
и равным a1
в случае справ-сти H1.Очевидно,
что если вел-на
(выбор. средняя) распр-на по норм. закону
с дисперсией 2/n
и мат.ож-ем, равным a
в случае справ-сти H0,
и равным a1
в случае справ-сти H1.Очевидно,
что если вел-на
![]() оказ.
достаточно малой, то это дает основ-е
предпочесть г-зуH0
г-зе H1.
При дост-но большом знач-и
оказ.
достаточно малой, то это дает основ-е
предпочесть г-зуH0
г-зе H1.
При дост-но большом знач-и
![]() более вероятна справ-сть гипотезыH1.
В кач. стат. критерия выбир. СВ. Z
= (x
с чертой – а)*(корень из n)/(ср.
кв. откл-е), распр. по норм. закону, причем
Mz
= 0 и Dz
=
1 в случае справ-сти гипотезы H0.
Если справедл. гипотеза H1,
то
Mz
= a*
= ( a1
– a
)
более вероятна справ-сть гипотезыH1.
В кач. стат. критерия выбир. СВ. Z
= (x
с чертой – а)*(корень из n)/(ср.
кв. откл-е), распр. по норм. закону, причем
Mz
= 0 и Dz
=
1 в случае справ-сти гипотезы H0.
Если справедл. гипотеза H1,
то
Mz
= a*
= ( a1
– a
)![]() /,
Dz
=
1.Если вел-на
/,
Dz
=
1.Если вел-на
![]() ,
получ. из выбор. данных, относ-но
велика, то и вел-наz
велика, что явл. свид-вом в пользу г-зы
H1.
Относ-но малые знач-я
,
получ. из выбор. данных, относ-но
велика, то и вел-наz
велика, что явл. свид-вом в пользу г-зы
H1.
Относ-но малые знач-я
![]() приводят к малым знач-ямz,
что свид-вует в пользу г-зы H0.
Отсюда следует, что д. б. выбрана правостор.
крит. область. По принятому уровню
знач-сти
(напр.,
= 0,05), используя то, что СВ z
распр-на по норм. закону, опр. знач-е Kкр
из ф-лы
= P(Kкр
<
z
<)
= ()
– (Kкр)
= 0,5 – (Kкр).Отсюда
Ф(Ккр)=(1-2альфа)/2.
Если в-на z,
получ. при выбор. знач-и
приводят к малым знач-ямz,
что свид-вует в пользу г-зы H0.
Отсюда следует, что д. б. выбрана правостор.
крит. область. По принятому уровню
знач-сти
(напр.,
= 0,05), используя то, что СВ z
распр-на по норм. закону, опр. знач-е Kкр
из ф-лы
= P(Kкр
<
z
<)
= ()
– (Kкр)
= 0,5 – (Kкр).Отсюда
Ф(Ккр)=(1-2альфа)/2.
Если в-на z,
получ. при выбор. знач-и
![]() ,
попад. в область принятия г-зы (z < Kкр),
то г-за H0
приним. Если в-на z
попад. в крит. область, то г-за H0
отверг. II. Если в предыд. задаче поставить
др. условие: H0:
M
= a;
H1:
M
= a1
,
a1
< a,
то здесь придется рассм. левостор. крит.
область. Здесь a*
= ( a1 – a
)
,
попад. в область принятия г-зы (z < Kкр),
то г-за H0
приним. Если в-на z
попад. в крит. область, то г-за H0
отверг. II. Если в предыд. задаче поставить
др. условие: H0:
M
= a;
H1:
M
= a1
,
a1
< a,
то здесь придется рассм. левостор. крит.
область. Здесь a*
= ( a1 – a
)![]() /,
а вел-на Kкр
опр. из ф-лы
= P(–
<z<
Kкр)
= (
Kкр)
–
(–)
= (
Kкр)
+ 1/2.Используя формулу –(
Kкр)
= (
–Kкр),
получаем: (
–Kкр)=(1-2альфа)/2.
Знач-я z,
вычисл. по выбор. данным, превыш. Kкр,
согласуются с г-зой H0.
Если в-на z
попад. в крит. область (z < Kкр),
то г-зу H0
следует отвергнуть, считая предпочт.
г-зу H1.III.
Рассмотрим теперь такую задачу: H0:
M
= a;
H1:
M
a.
В данном случае следует рассм. двустор.
крит. область. Крит. знач-е Kкр
опр-ся с пом. соотн-я P(–Kкр
< z
< Kкр)
= 1 –
= (
Kкр)
–
(
– Kкр)
= 2(
Kкр)
.Из этого соотн-я следует: (
Kкр)
= )=(1-альфа)/2.
/,
а вел-на Kкр
опр. из ф-лы
= P(–
<z<
Kкр)
= (
Kкр)
–
(–)
= (
Kкр)
+ 1/2.Используя формулу –(
Kкр)
= (
–Kкр),
получаем: (
–Kкр)=(1-2альфа)/2.
Знач-я z,
вычисл. по выбор. данным, превыш. Kкр,
согласуются с г-зой H0.
Если в-на z
попад. в крит. область (z < Kкр),
то г-зу H0
следует отвергнуть, считая предпочт.
г-зу H1.III.
Рассмотрим теперь такую задачу: H0:
M
= a;
H1:
M
a.
В данном случае следует рассм. двустор.
крит. область. Крит. знач-е Kкр
опр-ся с пом. соотн-я P(–Kкр
< z
< Kкр)
= 1 –
= (
Kкр)
–
(
– Kкр)
= 2(
Kкр)
.Из этого соотн-я следует: (
Kкр)
= )=(1-альфа)/2.
47.
Проверка гипотезы о равенстве
математических ожиданий двух нормально
распределенных случайных величин.
Предполож.,
что имеются случ. выборки х1,
х2,
..., хп и y1, y2,
..., ym знач-й
двух независ. нормально распред.
СВ ![]() и
и ![]() и
требуется проверить гипотезу
и
требуется проверить гипотезу ![]() о
рав-ве мат. ожиданий этих СВ. (а) Если
известно, что дисперсии случайных
величин и равны,
о
рав-ве мат. ожиданий этих СВ. (а) Если
известно, что дисперсии случайных
величин и равны, ![]() (значение
(значение ![]() неизвестно),
то можно получить след. объедин.несмещ.
оценку для
неизвестно),
то можно получить след. объедин.несмещ.
оценку для ![]()
![]() В
этом сл. s2/n и s2/m будут
несмещ. оценками для дисперсии выборочных
средних
В
этом сл. s2/n и s2/m будут
несмещ. оценками для дисперсии выборочных
средних ![]() и
и![]() ,
а сумма s2/n+s2/m –
несмещ. оценкой для дисперсии разности
средних
,
а сумма s2/n+s2/m –
несмещ. оценкой для дисперсии разности
средних ![]() .
Соотв-но, статистика
.
Соотв-но, статистика
![]() как
можно показать, будет иметь t-распред-е
с n+m-2
степенями свободы. Крит. область
уровня
как
можно показать, будет иметь t-распред-е
с n+m-2
степенями свободы. Крит. область
уровня ![]() для
проверки гипотезы
для
проверки гипотезы ![]() против
двустор. альтернативы
против
двустор. альтернативы ![]() будет
состоять из двух бесконечных
полуинтервалов
будет
состоять из двух бесконечных
полуинтервалов ![]() и
и ![]() ,
против одностор. альтернативы
,
против одностор. альтернативы ![]() -
из полуинтервала
-
из полуинтервала ![]() и
против альтернативы
и
против альтернативы ![]() -
из полуинт-ла
-
из полуинт-ла ![]() ,
где
,
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() обознач.
соотв. квантили t-распред-я
с n+m-2
степенями свободы.
обознач.
соотв. квантили t-распред-я
с n+m-2
степенями свободы.
(б)
Если нет оснований считать, что дисперсии
СВ и равны,
то для каждой из дисперсий ![]() и
и ![]() вычисл.
своя оценка
вычисл.
своя оценка![]() и
соотв-нно модифиц. статистика
критерия
и
соотв-нно модифиц. статистика
критерия![]() которая,
как можно показать, имеет t-распред-е
с числом степеней свободы, равным целой
части от 1/k,
где k выражается
след. формулой
которая,
как можно показать, имеет t-распред-е
с числом степеней свободы, равным целой
части от 1/k,
где k выражается
след. формулой
![]()
48.
Критерий согласия Пирсона о предполагаемом
законе распределения случайной величины.
1.)
Исходя из теоретического (предполагаемого
закона распределения), находим вероятности
рi
попадания СВ в каждый из заданных
интервалов таблицы, например в случае
нормального распределения
![]() .
.
2.)
Вычисляем значение 2
соответствующее опытным данным по
формуле:
![]()
3.) По табл. критических точек 2, учитывая число степеней свободы k=m-r-1, где m – число интервалов, r – число оцениваемых параметров в распределении (для нормального распределения r=2) – находим по таблице 2крит.
4.) Если 2вычисленное<2крит., то гипотеза о нормальном распределении принимается. Если же 2вычисленное>2крит., гипотеза отвергается.
Замечание: При нахождении 2крит. учитывается уровень значимости критерия, который обозначается (q). Уровень значимости критерия для технических задач обычно принимается =0,05. Он означает вероятность того, что событие не наступит при данных условиях.
49. Критерий согласия Колмогорова о предполагаемом законе распределения случайной величины. 1.) По результатам n – независимых опытов найти эмпирическую функцию распределения: F*(x)
2.) Определить максимум модуля: |F*(x)-F(x)| во всех точках.
3.)
Вычислить выборочную статистику
![]() .
.
4.) Сравниваем значения выборочн. с критическим значением , определенным по табл. 5.) Если выборочн<крит. – гипотеза принимается, если выборочн>крит. – гипотеза отвергается.
50. Основные понятия дисперсионного анализа. Однофакторный и двухфакторный дисперсионный анализ Дисперсионный анализ примен.для исслед-я влияния 1 или неск.кач. переменных на 1 завис.колич.пер-ную . В основе дисперс. анализа лежит предпол-е о том, что одни переменные могут рассматриваться как причины (независ. переменные): , а другие как следствия (завис.переменные). Независ. переменные наз. иногда регулир. ф-рами именно потому, что в эксперименте иссл-ль имеет возм-сть варьировать ими и анализ-ть получающийся рез-т.Осн. целью дисперс. анализа явл. исслед-е значимости различия между средними с пом. сравнения (анализа) дисперсий. Раздел-е общей дисперсии на несколько источников, позволяет сравнить дисперсию, вызванную различием между группами, с дисперсией, вызванной внутригрупп. изменчивостью. При истинности нулевой гипотезы (о равенстве средних в неск. группах наблюдений, выбранных из генер. совок-сти), оценка дисперсии, связанной с внутригруп. изменчивостью, д. б. близкой к оценке межгрупп. дисперсии. Сущность дисп. анализа закл. в расчленении общей дисперсии изуч. признака на отд. компоненты, обусловл. влиянием конкр. ф-ров, и проверке гипотез о значимости влияния этих ф-ров на исслед. признак. Сравнивая комп-ты дисперсии друг с другом посредством F—критерия Фишера, можно определить, какая доля общей вариативности результат. признака обусловлена действием регулир. ф-ров. Исходным мат-лом для дисп.анализа служат данные исслед-я 3 и более выборок: , которые могут быть как равными, так и неравными по численности, как связными, так и несвязными. По кол-ву выявляемых регулир. ф-ров дисп. анализ м. б. однофакт. (при этом изуч. влияние 1 фактора на рез-ты эксперимента), двухфакт. (при изучении влияния двух факторов) и многофакт. (позволяет оценить не только влияние каждого из факторов в отдельности, но и их взаимодействие). Дисп. анализ относится к группе параметрич. методов и поэтому его следует применять только тогда, когда доказано, что распред-е явл. нормальным. Дисп. анализ исп., если зависимая переменная измер. в шкале отношений, интервалов или порядка, а влияющие переменные имеют нечисловую природу (шкала наименований).
