28. Вер-ть попад-я в зад. Интервал нормально распред. Случ. В-ны. В-сть зад. Откл-я. Правило трех сигм.

Ф-ия распр. нормального распр. СВ Х выражается через ф-ию Лапласа по формуле:

В-сть попадания нормально распр. СВ Х в заданный интервал опр.ф-лой. Часто в задачах требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины Х от ее М(х) =а по абсол. величине меньше заданного полож. числа ε. Для этого исп. формула:

При реш-и многих важных практич. задач делают предпол-е, что СВ распределена по норм. закону. Возн. вопрос, на каком основании делается такое допущение. Для иссл-я этого вопроса рассм. одну характ. особ-сть норм. распред-я СВ. Найдем в-сти событий: |x-a|<σ ;|x-a|<2σ ; |x-a|<3σ Используем формулу:P(|x-a|<σ)=2Ф(1)=0,6826 P(|x-a|<2σ)=2Ф(2)= 0,9594 P(|x-a|<3σ)=2Ф(3)=0,9973 – это событие практически достоверное. Посмотрим в таблицу: из последнего соотношения следует, что практически все возможные значения норм. распр-я СВ x принадлежат интервалу (a-3σ; a+3σ)

Итак, правило трех σ утверждает, что с очень высокой вер-тью (0,998) практически все значения СВ сосредоточены в инт-ле (a-3σ;а+3σ)

29. Моменты случайной величины. Асимметрия. Эксцесс.

Среди числ. хар-к СВ важное значение имеют моменты, кот. делятся на начальные и центральные.

Начальный теор. момент ν порядка k НСВ X определяется равенством .Для ДСВ Х, принимает значение X1, X2, …,Xn с вероятностью P1, P2, …Pn.

Центр. теор. момент порядка k НСВ Х определяется рав-вом .

Очевидно, что

Следствия: 1. ν0=1, μ0=1 2. ν1=M(x), μ1=0 3. ν2=M(x²), μ2=D(x), μ2= ν₂-ν₁² 4. μ3=v₃-3v₁v₂+2v₁³.

Математическое ожидание М(Х), или первый начальный момент, характеризует среднее значение распределения случайной величины Х; второй центральный момент, или дисперсия D(X ), — степень рассеяния распределения Х

относительно М(Х).

Третий центр. момент служит для хар-ки асимм. распр и опр. по формуле . Эта величина наз. коэфф. ассим.

Четвертый центр . момент характ. крутость распр. и выражается через параметр, кот. наз. эксцессом. Эксцесс опр. по формуле .

30. Неравенство Маркова. Если СВ Х принимает неотрицательные значения, т.е. (х≥0, х_i≥0) и существует ее мат. ожидание M(x)=a, то для любого положительного числа а числа выполняются неравенства:

; .

31. Неравенство Чебышева. Если Х-СВ, мат. ожидание к-рой М(Х) = а, а дисперсия D(Х) конечна, то д/любого числа ε > 0 выполняются неравенства:

Если уточняется закон распределения, то соотв. можно найти и более точное значение вер-ти. Если СВ Х распр. по норм. закону, то хорошо известно правило трех σ, кот. утв, что с очень высокой вер-тью (0,998) практически все знач. СВ сосредоточены в инт-ле (a-3σ;а+3σ).

32. Теорема Чебышева. Если СВ-ы Х1, Х2….Хn попарно независимы и имеют мат. ожид. M(x1), M(x2)….M(xn) и дисперсии D(x1), D(x2)…..D(xn), кот. ограничены одной и той же констанотой С (P(X_i)=C), то при неогр. большом увел. числа n вып. неравенство:

Фактически эту формулу можно интерпретировать как сходимость по вер-ти ср. знач. величин к ср. знач. их мат. ожиданий

Вывод: среднее арифметическое достаточно большого числа СВ принимает значения, близкие к сумме их мат. ожиданий, т.е. как угодно мало отличается от постоянной величины a. (от неслучайных величин)

33. Теорема Бернулли. Значение закона больших чисел. Если вероятность наступления события А в каж-м из n повторных независимых испытаний постоянна, то при неограниченном увеличении числа n испытаний отн-я частота(частость) наст-я соб-я А стрем-ся по вер-ти к числу p, т.е. для>0Данное выражение представляет собой опр. вер-ти по Мизесу. Т-ма Б-ли явл-ся теор-ким обосн-ем для стат-го опр-я вер-ти.

Неравенство Бернулли:Пусть n исп-й Бернулли с вер-ю успеха p, q=1-p и m – число успехов. Тогда для>0

Общий смысл закона б.ч. — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.

На этом свойстве основаны методы оценки вероятности на основе анализа конечной выборки. Примером является прогноз результатов выборов на основе опроса выборки избирателей

4. Понятие о центральной предельной теореме.Суть центральной предельной теоремы (ЦПТ) в след.: если СВ Х представляет собой сумму большого числа взаимно независимых случ. в-н, влияние каждой из которых на всю сумму ничтожно мало, то х имеет расп-е, близкое к нормальному.

Центральная предельная теорема (ЦПТ) ( в формулировке Ляпунова А.М. для одинаково распред. СВ): Если попарно независимые СВ X1, X2, ..., Xn, ... имеют одинаковый закон распределения с конечными числовыми характеристиками M[Xi] =  и D[Xi] = 2, то при n   закон распределения СВ неограниченно приближается к норм. закону N(n, ). Следствие. Если в условии теоремы СВ, то при n  закон распределения СВ Y неограниченно приближается к нормальному закону N(, /).

35. Предмет и метод мат. статистики. МС – раздел мат-ки, кот. изуч. методы сбора, систематизации и обработки рез-тов набл-й с целью выявления стат. зак-стей. МС осн. на понятиях и р-тах ТВ и оперирует непосредственно с р-тами наблюдений над случ. явлением. Ее цель-оценить характер-ки генер. совок-ти по выборочным данным. Предметом МС явл. изуч-е случ. событий и случ. величин по р-там наблюд-й. Осн. задача МС сост. в получ-и выводов о массов. явлениях по данных наблюдения за ними. Др. задачами МС явл.: 1.указать способы сбора и группировки стат. сведений, получ. в р-те наблюдений или в р-те спец. поставл. экспер-тов; 2.разработать методы анализа стат. данных в зав-сти от целей иссл-я. Р-том наблюд-й над стат. совок-стью явл. стат. данные. Обработка стат. данных методами МС приводит к установл-ю опред. законом-стей, присущих массовым явл-ям.

36. Генеральная и выборочная совокупности. Способы отбора. Ген. сов-ть – это множество всех обслед. объектов. В ген. сов-ти выбирают часть объектов и изуч. их. Эта часть объектов наз. выброчной сов-тью. Т.о. в мат. статистике различают два вида наблюдений: сплошное, когда изучаются все объекты совокупности и несплошное (выборочное), когда изучается только часть объектов. Правильная орг-ия выборки явл. самой сложной частью стат. иссл. Правильная орг-ия выборки ведет к понятию репрезент. выборки,т.е. такой выборки, изуч. кот. дает адекватное предст. о ген. сов-ти.

Способы отбора можно подразделить на 2 вида:

1. Отбор, не требующий расчленения ген. сов-ти(случ. бесповт. и повт. отбор)

2. Отбор, при кот. ген. сов-ть разбивается на части (типический отбор, мех. отбор, серийный отбор). Бесповторная выборка – из генер. совок-ти элементы извлекаются и не возвращаются обратно. Если после извлечения элементов из совок-ти они фиксируются и возвращаются обратно – повторный отбор.

Считается, что одним из наиб. правильных способов выборки явл. случ. отбор из ген. сов-ти, т.е. элементы берутся наугад и каждый из них может быть отобран с одинаковой вероятностью. Кол-во объектов генер. или выбор. сов-ти называют объемом.

Сплошное набл. применяют когда объем генер. совок. небольшой.

37. Постр-е дискретного вар. ряда. Эмпир. функция распр-я и ее св-ва. Пусть для некот. сов-ти изуч. пр-к Х, кот. может быть описан числ, величинами. Обозначим возм. знач. пр-ка Х₁ , Х₂ ...Х­_m. Дискретный вариационный ряд (m-объем выборки) называется последовательностью. Из дикретного вар. ряда строится стат. ряд. распр., кот. форм. след. образом: 1. среди всех вар-тов выбир. разл. и упорядоч. по возраст, а также считается, сколько раз каждый член стат. ряда встреч. в дискретном вар. ряду.2. находим размах выборки. (3. иногда вместо стат. ряда записывается ряд, в кот. во второй строке стоят частости) Стат. распред. можно изобр. графически. Для этого на Ох наносят xi, а на Оу – частоты mi. Соединив точки частот, получим ломаную, кот. наз-ся полигоном распр. В завис-ти от того, какие знач. принимает признак стат. распред., вариац. ряды дел. на Дискретные (варианты приним. конкр. значения) и Интервальные (варианты изменяются непрерывно в некот.интервале). Эмпир.функция распр-я.Пусть известно стат. распр-е колич. признака Х; n_x – число наблюдений, при кот-х наблюдалось знач-е признака, меньшее x , т.е. Х< x; n – общее число наблюдений (объём выборки). Тогда относ. частота события Х< x есть n _х/n. При изм-и x меняется и n_х /n, т.е. относительная част. n_х /n является функцией x . Так как эта функция находится эмпирически. (т.е. получ. опытным) путём, то её наз. эмпирической. Итак , эмпир. функцией распр-я (функцией распр-я выборки) наз. функция опред. для каждого знач-яxR относ. частоту события Хx. Т.к. в этой ф-ле n_х – число вариант, меньших x, поэтому для расчетов удобна ф-ла вида .

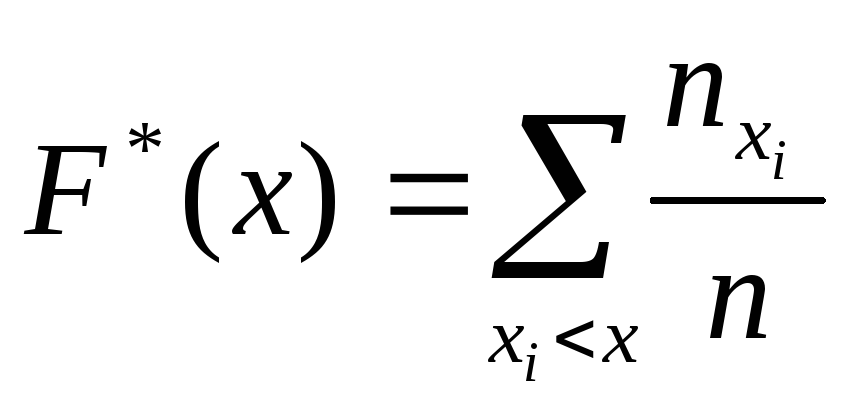38. Построение интерв. вариац. ряда. Гистограмма частот и относ. частот. При большом объеме выборки ее элементы объед. в группы (разряды, интервалы), представляя р-ты опытов в виде интерв. стат. ряда. Для этого весь диапазон значений СВ (от xmin до xmax ) разбивают на k интервалов одинак. длины h (обычно k меняется от 5 до 20). Число интервалов рекомендуют брать согласно формуле Стерджеса k 13,93ln n Затем подсчит. частоты ni (или относит. частоты i ) знач-й выборки, попавших в выдел. интервалы. Величина ni/h наз. плотностью частоты, а i/h – плотностью относ. частоты. Пусть xi* – середина i -го интервала, ni – число эл-тов выборки, попавших в i -й интервал. Таким образом, получим группиров. стат. ряд, в верхней строке которого записаны середины соотв. интервалов xi*: xix1x2…xkni n1 n2 … nk.

Д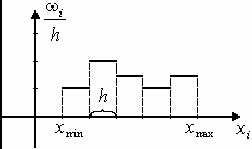ля граф. представления интерв. стат. распределений принято использовать гистограмму частот и гистограмму относ. частот. Гистогр. частот наз. ступенчатую фигуру, сост. из прямоуг., основаниями кот служат частичные инт-лы длиною h, а высоты равны отношению n_i/h_. Гистограммой относ. частот интервального стат. ряда наз. ступенчатая фигура, составл. из прямоугольников, постр. на интервалах группировки длины h и высоты i/h так, что площадь каждого прямоугольника равна относительной частоте i.Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки длиной i/h параллельно оси ординат. Очевидно, площадь i -го частичного прямоугольника равна i – относительной частоте вариант, попавших в i -ый интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот (т.е. равна 1), а площадь гистограммы частот равна объему выборки n .

39. Выборочная средняя, выборочная дисперсия и их свойства Выборочная средняя. Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема n. Выборочной средней называют среднее арифметическое значение признака выборочной совокупности. Если все значения признака выборки различны, то если же все значения имеют частоты n1, n2,…,nk, то Выборочная средняя является несмещенной и состоятельной  оценкой генеральной средней. Замечание: Если выборка представлена интервальным вариационным рядом, то за xi принимают середины частичных интервалов.

Выборочная дисперсия. Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения, вводят сводную характеристику- выборочную дисперсию. Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения . Если все значения признака выборки различны, то  если же все значения имеют частоты n1, n2,…,nk, то

40. Точечное оцен-е числ. хар-к СВ. Состоят-сть, эффективность, несмещенность оценки. Исправл. выбор. дисперсия. Точ. оценкой хар-ки θ наз. некот. ф-цию  р-тов наблюд-й, знач-я кот-ой близки к неизв. хар-ке θ генер. совок-сти. Для постр-я оценки нужны критерии:1.Несмещеность. Оценка  наз. несмещ., если её мат. ожид-е равно оцениваемой хар-ке СВ: ,   т. е. если она не дает системат. ошибки. 2.Состоятельность.  Оценка наз. состоят., если при увел-и числа набл-й оценка сходится по вероятности к искомой вел-не, т. е. для любого сколь угодно малого   . Состоят-сть означ., что оценка, постр. по большому числу наблюд-й, имеет меньший разброс (дисперсию), т. е. . 3.Эф-ть. Желательно иметь оценки, кот-е имеют наим. дисперсию среди всех оценок, постр. по n набл-ям. Такие оценки наз. эффективн..

Точечная оценка мат. ожидания. Пусть изуч. СВ Х с МX=а и DX,причем оба параметра неизв.Статистика (т.е. ф-ия ) наз. точечной оценкой парматера. Др. словами, точечная оценка – это конкр. число, опр. по выборке.

Пусть Х₁,Х₂,...,Х_n – выборка объема n. Тогда сост. и несмещенной оценкой МХ явл выборочная средняя Х (с чертой сверху). Док-во этого соотн. осн. на теореме Чебышева. На практике, к.п., в кач-ве оценки МХ исп. ср. арифм.

Точечная оценка дисперсии. Доказано, что D_вХ связана с DX СВ Х след. формулой:

D_ВХ=, т.е. М(DвХ)=DX,т.е. DвХ явл. смещенной оценкой дисперсии. Поэтому,чтобы получить несмещ. оценку дисп, DвХ испраляют, умножив ее на и обозн... Исправл. выборочная дисп. явл. несмещенной, состоятельной оценкой дисперсии.