13.Формула Пуассона для редких событий.

Когда n велико, а р мало, то вычисления по формуле Бернулли крайне затруднительны. Поэтому для вычисления вер-тей применяются приближенные формулы, кот. называются ассимптотическим. одной из таких формул явл. ф. Пуассона для редких событий:

Эта формула дает удовлетворительное приближение для p<=0,1и np<=10 . При больших np рекомендуется применять формулы Лапласа.

14. Дискретная случайная величина, ее закон распределения. Многоугольник распределения.

Часто р-том случ. эксперимента явл. число.Естественно рассм. случайную величину как ф-ию, заданную на множестве исходов случ. эксперимента.

СВ условно разделяют на дискретные и непрерывные.

СВ называется дискретной, если множество ее возможных значений конечно или счетно. Например, число бросаний монеты до появления герба или число выпавших очков при бросании игрального кубика.

ДСВ полностью характеризуется заданием закона распределения, кот. опис. с помощью матрицы, сост. из двух строк: строка возм. знач. СВ и строка вер-тей, с кот. эти значения могут появляться. [Пример с кубиком] Т.к. в верхней строке перечислены все возм. знач. СВ, то эти значения образ. полную г-пу событий. Следовательно сумма вер-тей равна 1.

Ряд распределения дискретной случайной величины можно изобразить

графически в виде полигона или многоугольника распределения вероятностей.

Для этого по горизонтальной оси в выбранном масштабе нужно отложить зна-

чения случайной величины, а по вертикальной — вероятности этих значений,

тогда точки с координатами (xi , pi) будут изображать полигон распределения

вероятностей; соединив же эти точки отрезками прямой, получим многоуголь-

ник распределения вероятностей.

15. Функция распределения вероятностей случайной величины и ее свойства.

Ф-ия распр. – это вер-ть того, что СВ принимает значения, меньше, чем х. Функцией распределения (ФР) (или интегральная ф-ия распределения) СВ X называется числовая функция F(x) = P{X < x}, определенная для любых x  R.

Св-ва ФР:

1. 0  F(x)  1, т.к. по опр. это вер-ть;

2. F(x₁)  F(x₂), если x₁  x₂, т.е. F(x) - неубывающая функция;

3. 

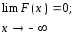
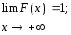
4. P{a  X  b} = F(a) - F(b).

16. Математическое ожидание дискретной случайной величины и его свойства.

Одной из важнейших хар-к СВ явл. мат.ожидание, кот по своему смыслу характ. ср. знач. СВ.

Для ДСВ МХ находится по формуле:

m_X = M[X] = M(X) = x1 p1+ x2 p2+...+ xn pn=

Свойства математического ожидания:

1. M[C] = C, где С - константа;

2. M[CX] = CM[X];

3. M[X+-Y] = M[X]+-M[Y], для любых СВ X и Y;

4. M[XY] = M[X]M[Y]

5. М[X-M(X)]=0 – мат. ожидание отклонения СВ от ее мат. ожидания равно 0.

17. Дисперсия дсв и ее св-ва. Среднее квадр. Отклонение.

Вадной хар-кой СВ явл. хар-ка разброса значений СВ около мат.ожидания. Эта хар-ка называется дисперсией DX.

По определению дисперсия – это мат. ожидание квадрата отклонения СВ от ее MX:

Если Х — ДСВ, то дисперсию вычисляют по следующим формулам:

Св-ва дисперсии:

1.

2.

3.

4.

Среднее квадратическое отклонение дискретной случайной величины есть арифметическое значение корня квадратного из ее дисперсии:

Среднее квадратическое отклонение характеризует степень отклонения случайной величины от ее математического ожидания и имеет размерность

значений случайной величины

18. Биномиальный закон распределения и его числовые характеристики. Пусть проводится n независимых испытаний. В результате каждого из которых возможны 2 исхода: А – успех с вероятностью p, или - неуспех с вероятностью q = 1-p. Дискретная СВ X , ,характ. число появления события А принимает значения Х=m c вер-тями

P(X=m)=, где p>0, q>0, m 0,n. Для бин. з.р. доказано, что мат.ожидание M(X)= np , дисперсия среднее квадратическое отклонение -

19. Геометрическое распределение. Геометрическим распределением называется распределение ДСВ X, кот. прин. только полож. знач., при этом вер-ти того, что ДСВ Х примет знач. равное k считаются по формуле

Т.о геометр.распр. есть испытание по схеме Бернулли до первого положительного исхода.

Вероятности образуют бесконечно убывающую геометрическую прогрессию со знаменателем q=1-p (с этим связано название). Для геометр. закона распр. доказано, что мат. ожидание равно M(x)=1/p , дисперсия равна D(x)=

20. Гипергеометрическое распределение. Пусть имеется N элементов, из кот-х М эл-тов облад. некот-м признаком А. Извлек. случ. образом без возвращ-я n эл-тов. X – ДСВ, число эл-тов, облад. признаком А, среди отобр. n эл-тов. Вер-ть того, что Х =k опред. по формуле: P(x=k)=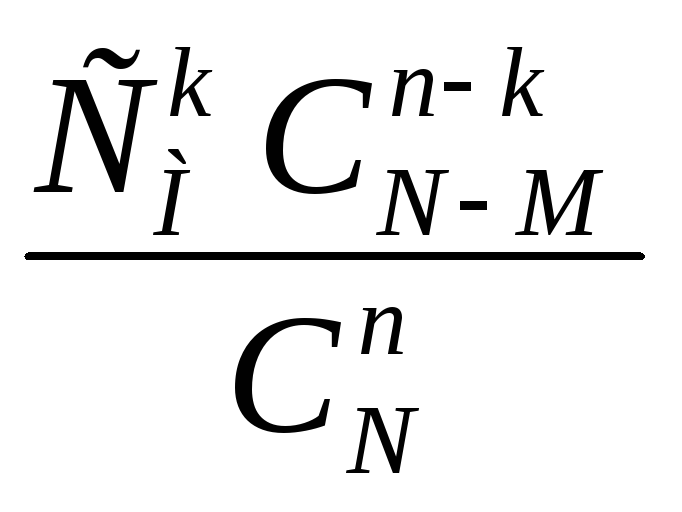Для гипергеометр. распр. доказано, чтоM(x)= D(x)=

21. Формула Пуассона. Распределение Пуассона. Фактически, закон Пуассона – это биномиальное распр при большом числе испытаний n и малой вер-ти наступления события в каждом из испытаний, поэтому з-н Пуассона часто называют з-н редких явлений. ДСВ Х распр. по закону Пуассона, если она прин. знач. 0,1,2,..m,... с вер-тями ,где λ=np (среднее число появл-я события в n испытаниях), m – число появления события в n независимых испытаниях; m приним. значения 0,1,2,…,n. Мат. ожидание и дисперсия СВ, распределенной по закону Пуассона, совпадают и равны параметру λ : M(X)=λ, D(X)=λ.

22. Непрерывная случайная величина, плотность распределения вероятностей непрерывной случайной величины и ее свойства. Случ. вел-на Х наз. непрерывной, если ее функция распред-я непрерывна в любой точке и дифференцируема всюду, кроме отдельных точек. Пример: рост человека. Теорема: Вероятность любого отдельного знач-я непрер. случ. вел-ны равна нулю: P(X=x₁)=0. Для НСВ P(x₁< X < x₂)=F(x₂)-F(x₁). НСВ как и ДСВ задается функцией распр. Однако,такой способ задания неперыв.СВ не единств. Для НСВ ввод. понятие плотности вер-ти. Р(Х)). Свойства: 1.p(x)≥0 для люб, т.к. F(x) явл. неубывающей ф-ей.

2.Вер-ть попадания НСВ в инт-вал [а,b]вычисляется во формуле

3. и

. График ф-ии p(x) называется кривой плотности вер-ти.

23. Математическое ожидание и дисперсия непрерывной случайной величины Мат.ожид. НСВ Х, знач., кот. х принадлежат () с плотностью вероят.р(х), вычисл. по формуле:(требуется абсолют.сходимость интеграла.) Если НСВ X определена на[],то мат.ожид. опред. по формуле

Дисперсия НСВ X, знач. кот. принадлежат инт-лу ()с плотностью вер-ти р(Х) вычисляется по формуле:

(требуется абс. сход. интеграла)

Если все знач. НСВ принадлежат инт-лу (), то дисперсия вычисл.по формуле:

Или равносильным рав-вом:

24. Равномерный закон распределения и его числовые характеристики Непр. случ. велич.х распред. равномерно на отрезке [а;b], если её плотность вероятности р(х) постоянна на этом отрезке и равна 0 вне его:

Р(х)= {1/ (b-a), при а< =х<=b,

{О, при х<а, х>b

Пример: ожидание транспорта на остановке.

Функция распред. случайн. величины, распред-ой по равномерн. закону, имеет вид:

F(x)= { O, x<=a,

{(x-a)/(b-a), a<=x<=b,

{1, x>b

Мат. ожидание, дисперсия, средн. кв. откл-е:МХ=(а+b)/2; DХ=,

25. Показательный закон распределения и его числовые характеристики. Непрерывная СВ Х имеет показ. (экспоненциальное) распределение с параметром λ >0, если ее плотность распред-я имеет вид:

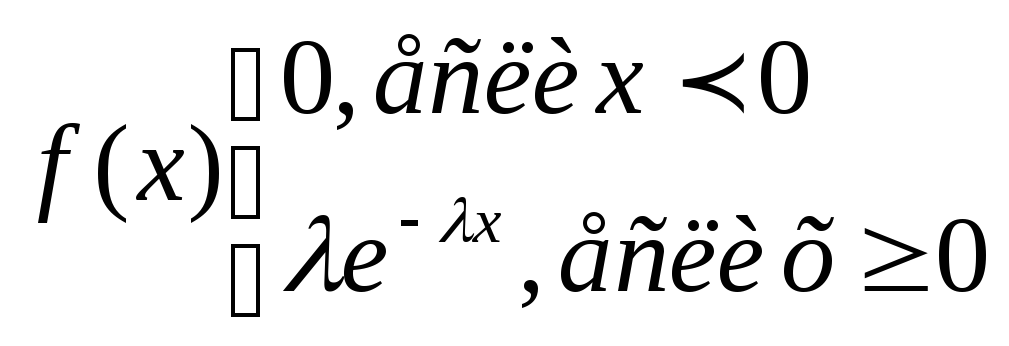
Ф-ция распределения СВ, распределенной по показ. з-ну:

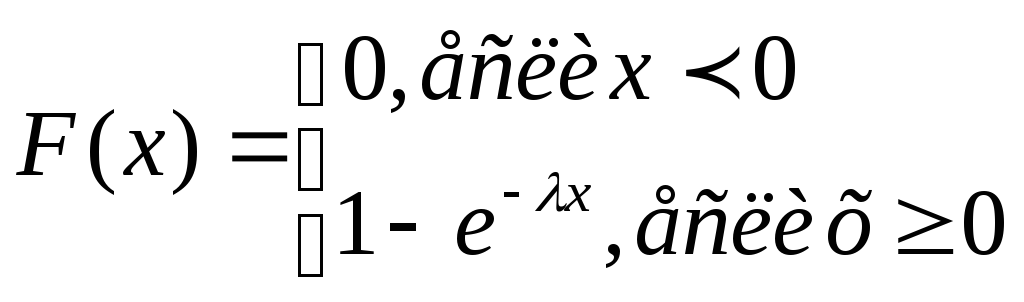
Показательному распределению обычно подчиняется время ожидания в очереди. Вероятность попадания случайной величины Х на интервал (α;β)

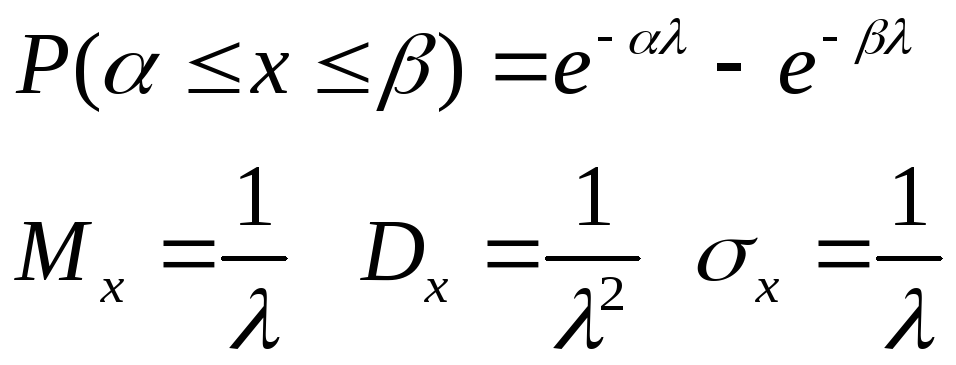
26. Нормальный закон распределения. Влияние параметров распределения на вид нормальной кривой. Непрерывная случайная величина X имеет нормальный закон распределения с параметрами а и , если её плотность вероятности  имеет вид p(x)=  Кривая нормального распределения  p(x)  (нормальная кривая или кривая Гаусса) приведена на рисунке.

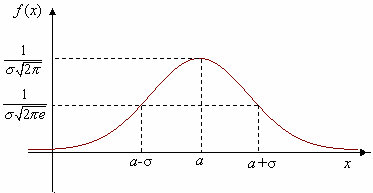
В точке х=a функция достигает своего максимума, кот. равен График симметр. относит. а. При изменении параметра а форма кривой не меняется, а ее график сдвигается влево или вправо. При изменении параметра σ меняется форма нормальной кривой: с увеличением параметра σ кривая должна приближаться к 0Х и растягиваться вдоль этой оси, а с уменьшением σ кривая стягивается к прямой х=а.

27. Числовые характеристики случайной величины, имеющей нормальное распределение. Непрерывная случайная величина X имеет нормальный закон распределения с параметрами а и , если её плотность вероятности p(x) имеет вид p(x)=  : Математическое ожидание случайной величины X, распределённой по нормальному закону, равно параметру а этого закона, а её дисперсия - квадрату параметра , т.е. Величина М(Х) называется также центром рассеяния, а среднеквадратичное отклонение характеризует ширину кривой распределения. С возрастанием максимальная ордината кривой убывает, а сама кривая становится более пологой, растягиваясь вдоль оси абсцисс, тогда как при уменьшении кривая вытягивается вверх, одновременно сжимаясь с боков